Unit outcomes

By the end of this unit you will be able to:

• Define and apply mechanical power.

What you should know

Before you start this unit, make sure you can:

• Define and calculate work and nett work. Refer to unit 1 if you need help with this.
• State and apply the work-energy theorem. Refer to unit 2 if you need help with this.

Introduction

In the previous units we have defined and used the concepts of energy and work. We know that work can be defined as the energy transferred by a force. But what about how quickly this energy is transferred? In other words, what about how quickly work is done?

Think of the following scenario. Two cars line up at the start of a race. One is an ordinary road car and the other is a sports car. Both cars can accelerate to [latex]\scriptsize 100~\text{km/h}[/latex] from rest. The ordinary road car can do it in [latex]\scriptsize 16~\text{s}[/latex]. The sports car can do it in [latex]\scriptsize 3.5~\text{s}[/latex]. If we assume that both cars have the same mass ([latex]\scriptsize 950~\text{kg}[/latex]), which car’s engine will do more work? Which car’s engine is more powerful?

What is power?

You may recognise the scenario above from the first question in the unit 1 assessment and therefore already know that the work done by both engines (ignoring wind resistance and friction) is the same. Remember that this is based on the work-energy theorem. We know that [latex]\scriptsize W_{net} = \Delta E_k[/latex]. As both cars experience exactly the same change in kinetic energy (both cars accelerate from [latex]\scriptsize 0~\text{m.s}^{-1}[/latex] to [latex]\scriptsize 27.78~\text{m.s}^{-1})[/latex], the net work done is the same.

But the sports car is able to do this work far quicker. We would say that it has a more powerful engine. This everyday use of the word ‘power’ is very similar to the physics use. We call the rate at which work can be done power. Therefore, [latex]\scriptsize P = \displaystyle \frac{W}{t}[/latex].

In unit 1, we calculated that the net work done by both engines is [latex]\scriptsize 366~570.99~\text{J}[/latex]. However, what is the power of each engine?

The road car:
[latex]\scriptsize P = \displaystyle \frac{W}{t} = \displaystyle \frac{366~570.99~\text{J}}{16~\text{s}} = 22~910.69~\text{W}[/latex]

The sports car:
[latex]\scriptsize P = \displaystyle \frac{W}{t} = \displaystyle \frac{366~570.99~\text{J}}{3.5~\text{s}} = 104~734.57~\text{W}[/latex]

The unit for power is joules per second ([latex]\scriptsize \displaystyle \frac{\text{J}}{\text{s}}[/latex] or [latex]\scriptsize \text{J.s}^{-1}[/latex]). However, the more common unit of power is the watt ([latex]\scriptsize \text W[/latex]); [latex]\scriptsize 1 \text{J.s}^{-1} = 1~\text{W}[/latex].

Clearly, the sports car engine is far more powerful than the road car engine. It can do the same amount of work in a far shorter time.

Using the definition of work, we can easily derive an alternative expression for power:
[latex]\scriptsize P =\displaystyle \frac{W}{t}= \displaystyle \frac{F \Delta x \cos \theta}{t}[/latex]

If the force and the change in displacement are in the same direction then:
[latex]\scriptsize P = \displaystyle \frac{F \Delta x}{t}[/latex]

But [latex]\scriptsize \displaystyle \frac{\Delta x}{t}[/latex] is the definition of velocity. Therefore:
[latex]\scriptsize P = Fv[/latex]

Note that if the force and velocity are in the opposite direction then power will be negative. Like work, power is not a vector. It only has magnitude.

Example 3.1

Calculate the power required for a [latex]\scriptsize 20~\text{N}[/latex] force to slide a [latex]\scriptsize 100~\text{kg}[/latex] box over a frictionless surface at a speed of [latex]\scriptsize 3~\text{m.s}^{-1}[/latex].

Solution

[latex]\scriptsize F = 20~\text{N}[/latex]
[latex]\scriptsize V = 3~\text{m.s}^{-1}[/latex]
We need to calculate the power required.

[latex]\scriptsize \begin{align*} P &= Fv\\ &= 20~\text{N} \times 3~\text{m.s}^{-1}\\ &= 60~\text{W} \end{align*}[/latex]

[latex]\scriptsize 60~\text{W}[/latex] are needed for a force of [latex]\scriptsize 20~\text{N}[/latex] to move a [latex]\scriptsize 100~\text{kg}[/latex] box across at frictionless floor at [latex]\scriptsize 3~\text{m.s}^{-1}[/latex].

Note: The weight of the box (its mass multiplied by the force of gravity) acts at right angles to the direction of motion of the box. Therefore, it does not contribute to the work done and hence the power needed.

Example 3.2

Question adapted from Everything Science Grade 12 Worked example 12 page 246

A forklift lifts a crate of mass [latex]\scriptsize 100~\text{kg}[/latex] at a constant velocity to a height of [latex]\scriptsize 8~\text{m}[/latex] over a time of [latex]\scriptsize 4~\text{s}[/latex]. The forklift then holds the crate in place for [latex]\scriptsize 20~\text{s}[/latex].

1. Calculate how much power the forklift exerts in lifting the crate?
2. How much power does the forklift exert in holding the crate in place?

Solutions

1. .
   [latex]\scriptsize \begin{align*} m_{crate} &= 100~\text{kg}\\ h_{crate} &= 8~\text{m}\\ t &= 4~\text{s} \end{align*}[/latex]
   .
   We need to calculate the power required to lift the crate.
   [latex]\scriptsize \begin{align*} P &= \displaystyle \frac{W}{t}\\ &= \displaystyle \frac{F \Delta x}{t}\\ &= \displaystyle \frac{m_{crate}\cdot g \times h_{crate}}{t}\\ &= \displaystyle \frac{100~\text{kg} \times 9.8~\text{m.s}^{-2} \times 8~\text{m}}{4~\text{s}}\\ &= 1~960~\text{W} \end{align*}[/latex]
2. While the crate is being held, there is no displacement and so the work done is zero. If no work is done, then no power is exerted.

Example 3.3

A [latex]\scriptsize 55~\text{kg}[/latex] athlete trains by doing stair sprints – running up a flight of stairs. From rest, she runs up three flights of stairs each [latex]\scriptsize 2.5~\text{m}[/latex] in height in [latex]\scriptsize 7.2~\text{s}[/latex]. If her final velocity is [latex]\scriptsize 7~\text{m.s}^{-1}[/latex] what is her power output?

Solution

Her total work will be the increase in her kinetic energy plus her increase in gravitational potential energy. Therefore [latex]\scriptsize W = \Delta E_k + \Delta E_p[/latex]. We are told that she starts from rest and we can assume that her initial gravitational potential energy is also zero (relative to her gravitational potential energy at the top of the stairs).

[latex]\scriptsize \begin{align*} W &= \Delta E_k + \Delta E_p\\ \therefore W &= (E_{kf} – E_{ki})+(E_{pf} – E_{pi})\\ &= (E_{kf} – 0) + (E_{pf} - 0)\\ &= \displaystyle \frac{1}{2} mv^2 + mgh \end{align*}[/latex]

[latex]\scriptsize \begin{align*} v &= 7~\text{m.s}^{-1}\\ m &= 55~\text{kg}\\ g &= 9.8~\text{m.s}^{-2}\\ h &= 3 \times 2.5~\text{m} = 7.5~\text{m}\\ W &= \displaystyle \frac{1}{2} \times 55~\text{kg} (7~\text{m.s}^{-1})^2 + 55~\text{kg} \times 9.8~\text{m.s}^{-2} \times 7.5~\text{m}\\ &= 5~390~\text{J} \end{align*}[/latex]

She does [latex]\scriptsize 5~390~\text{J}[/latex] of work in [latex]\scriptsize 7.2~\text{s}[/latex]. Therefore, her power output is [latex]\scriptsize P = \displaystyle \frac{W}{t} = \displaystyle \frac{5~390~\text{J}}{7.2~\text{s}} = 748.61~\text{W}[/latex].

Note that only [latex]\scriptsize 1~347.5~\text{J}[/latex] of work went into increasing her velocity from rest to [latex]\scriptsize 7~\text{m.s}^{-1}[/latex]. The bulk of the work ([latex]\scriptsize 4~042.5~\text{J}[/latex]) was required to lift her [latex]\scriptsize 7.5~\text{m}[/latex]. This is why stair sprints are such effective workouts.

Exercise 3.1

1. Does the work required to lift a book to a high shelf depend on how fast you lift it? Does the power required to lift the book depend on how fast you lift it? Explain.
2. A winch designed to be mounted on a truck is advertised as being able to exert a [latex]\scriptsize 6.8 \times 10^3~\text{N}[/latex] force and to develop a power of [latex]\scriptsize 0.30~\text{kW}[/latex]. How long would it take the truck and the winch to pull an object [latex]\scriptsize 15~\text{m}[/latex]?
3. An elevator motor lifts a total mass of [latex]\scriptsize 1.1 x 10^3~\text{kg}[/latex] a distance of [latex]\scriptsize 40.0~\text{m}[/latex] in [latex]\scriptsize 12.5~\text{s}[/latex] at a constant velocity. How much power does the elevator motor generate during this period?
4. A windmill is used on a farm to pump water out of a well. The water flows up [latex]\scriptsize 37~\text{m}[/latex] above the well water level, before being directed to the dam. The water is pumped at [latex]\scriptsize 2~\text{m.s}^{-1}[/latex].
   
   1. Calculate how much energy is necessary to pump [latex]\scriptsize 90~\text{kg}[/latex] of water out of the ell to a height of [latex]\scriptsize 37~\text{m}[/latex].
   2. It is necessary to pump at least [latex]\scriptsize 90~\text{kg}[/latex] of water per minute. What is the minimum power that the windmill must produce?
   3. The farmer wants to modernise the farm. The farmer decides to buy a [latex]\scriptsize 0.5~\text{kW}[/latex] petrol water pump. Will the petrol water pump be able to pump at the required rate?

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• Power is the rate at which work is done.
• The unit for power is joules per second ([latex]\scriptsize \text{J.s}^{-1}[/latex]), however, the more common unit of power is the watt ([latex]\scriptsize \text{W}[/latex]); [latex]\scriptsize 1 \text{J.s}^{-1} = 1~\text{W}[/latex].
• If force and velocity are in the opposite direction, then power will be negative.
• Like work, power is not a vector. It only has magnitude.

Unit 3: Assessment

Suggested time to complete: 45 minutes

Question 1 is adapted from NC(V) Grade 12 Paper 1 February 2019 question 8

1. A farmer irrigates his crops using water drawn from a storage tank. The water falls by gravity down through the pipe at a rate of [latex]\scriptsize 0.05~\text{m}^3\text{.s}^{-1}[/latex]. The water falls through a height of [latex]\scriptsize 8~\text{m}[/latex]. The mass of [latex]\scriptsize 1~\text{m}^3[/latex] of water is [latex]\scriptsize 1 \times 10^3~\text{kg}[/latex]. Ignore the effects of friction.
   
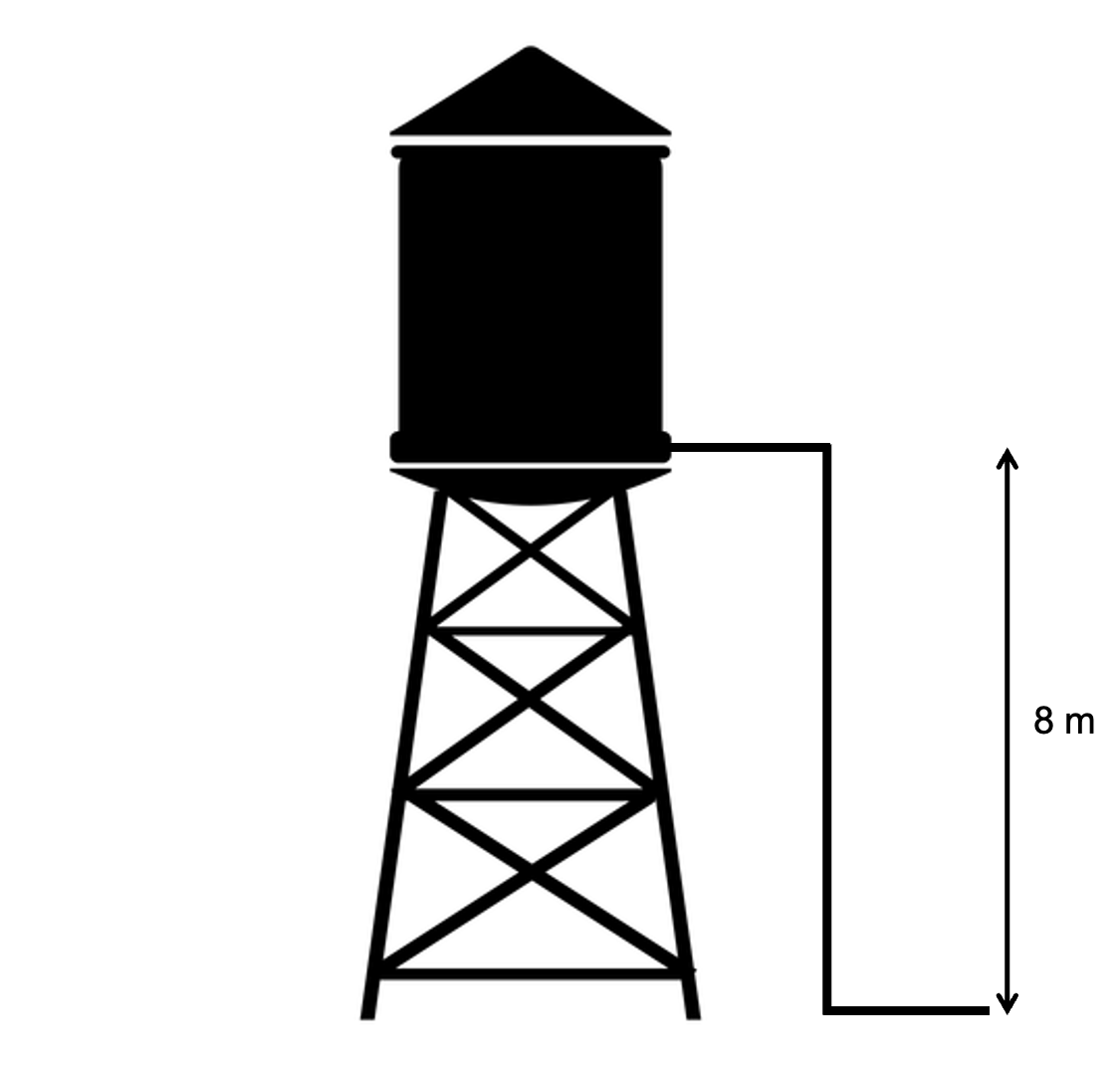
   1. Calculate the mass of water that flows through the downpipe each second.
   2. State the principle of conservation of mechanical energy.
   3. Using this principle, calculate the kinetic energy of the mass of water in a. above as the water reaches the bottom of the downpipe.
   4. The farmer decides to install a small hydro-electric generator at the bottom of the downpipe. Assume that the generator is able to convert [latex]\scriptsize 75\%[/latex] of the maximum kinetic energy gained by the water into electricity. Calculate the electrical power output of the generator.
2. A cable car has a mass of [latex]\scriptsize 3~000~\text{kg}[/latex] when fully laden. An electrical motor is used to pull the cable car up from the lower base station (at [latex]\scriptsize 366~\text{m}[/latex] above sea level) to the top of the mountain, which is [latex]\scriptsize 1~066~\text{m}[/latex] above sea level. The motor can deliver a maximum of [latex]\scriptsize 88~\text{kW}[/latex]. It takes seven minutes for the cable car to move from the lower base station to the top of the mountain.
   1. Define power.
   2. If the motor operates at maximum power output, calculate the electrical energy used by the motor to pull the cable car.
   3. Calculate the gain in gravitational potential energy of the fully laden car when it moves from the bottom station to the top station. Compare your answer with the value calculated in the previous question and explain the difference.
   4. Should the braking mechanism of the fully laden car fail while it is at rest at the top of the station, at what speed will the car strike the bottom station, if during the descent, the car loses [latex]\scriptsize 6 \times 10^6~\text{J}[/latex] of mechanical energy in doing work against friction?
3. Hikers climb to the top of a waterfall that is [latex]\scriptsize 948~\text{m}[/latex] high. [latex]\scriptsize 6 \times 10^4~\text{kg}[/latex] of water falls from the top of the waterfall each minute. (Ignore air resistance and any other frictional forces).
   1. Define gravitational potential energy.
   2. Calculate the gravitational potential energy of [latex]\scriptsize 6 \times 10^4~\text{kg}[/latex] of water at the top of the waterfall, relative to the bottom of the waterfall.
   3. The gravitational potential energy stored in this water could be used to turn a turbine connected to an electrical generator at the bottom of the falls. Describe the energy conversion that takes place in a generator.
   4. If [latex]\scriptsize 80\%[/latex] of the power that the water has owing to its gravitational potential energy is converted into electrical power, calculate the output power of the generator?
   5. What would be the average kinetic energy of a kilogram of water when it reaches the bottom of the waterfall?

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. Work is purely a function of force and distance. It does not matter how fast you lift the book. The total amount of work done is the same. Power, however, is the rate at which work is done. Therefore, the faster your raise the book, the more power you deliver.
2. .
   [latex]\scriptsize \begin{align*} P &= 0.3~\text{kW} = 300~\text{W}\\ F &= 6.8 \times 10^3~\text{N}\\ W &= F \Delta x\\ &= 6.8 \times 10^3~\text{N} \times 15~\text{m}\\ &= 102~000~\text{J}\\ P &= \displaystyle \frac{W}{t}\\ \therefore t &= \displaystyle \frac{W}{P}\\ &= \displaystyle \frac{102~000~\text{J}}{300~\text{W}}\\ &= 340~\text{s} \end{align*}[/latex]
3. During this period, there is no change in the velocity of the lift. Therefore, the lift does not gain any kinetic energy. The only work done is to overcome the weight of the lift. This work is exactly equal to the weight of the lift. There is acceleration hence no net force.
   [latex]\scriptsize \begin{align*} m &= 1.1 \times 10^3~\text{kg}\\ \Delta x &= 40~\text{m}\\ t &= 12.5~\text{s}\\ W &= F \Delta x\\ &= mg \Delta x\\ &= 1.1 \times 10^3~\text{kg} \times 9.8~\text{m.s}^{-1} \times 40~\text{m}\\ &= 431~200~\text{J}\\ P &= \displaystyle \frac{W}{t}\\ &= \displaystyle \frac{431~200~\text{J}}{12.5~\text{s}}\\ &= 34~496~\text{W} \end{align*}[/latex]
4. .
   1. The water is given potential energy and kinetic energy as its velocity is increased from
      [latex]\scriptsize 0~\text{m.s}^{-1}[/latex] to [latex]\scriptsize 2~\text{m.s}^{-1}[/latex].
      [latex]\scriptsize \begin{align*} h &= 37~\text{m}\\ v &= 2~\text{m.s}^{-1}\\ m &= 90~\text{kg}\\ W &= \Delta E_k + \Delta E_p\\ &= \displaystyle \frac{1}{2} mv^2 + mgh\\ &= \displaystyle \frac{1}{2} \times 90~\text{kg} \times (2~\text{m.s}^{-1})^2 + 90~\text{kg} \times 9.8~\text{m.s}^{-2} \times 37~\text{m}\\ &= 32~814~\text{J} \end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*} W &= 32~814~\text{J}\\ t &= 60~\text{s}\\ P &= \displaystyle \frac{W}{t}\\ &=\displaystyle \frac{32~814~\text{J}}{60~\text{s}}\\ &= 546.9~\text{W} \end{align*}[/latex]
   3. The [latex]\scriptsize 0.5~\text{kW}[/latex] pump will only be able to produce [latex]\scriptsize 500~\text{W}[/latex] of power. Therefore, it will be insufficient to pump [latex]\scriptsize 90~\text{kg}[/latex] of water a minute as this requires a power output of [latex]\scriptsize 546.9~\text{W}[/latex].

Back to Exercise 3.1

Unit 3: Assessment

1. .
   1. [latex]\scriptsize 0.05~\text{m}^3[/latex] flows every second. If [latex]\scriptsize 1~\text{m}^3[/latex] has a mass of [latex]\scriptsize 1~000~\text{kg}[/latex], then [latex]\scriptsize 0.05~\text{m}^3[/latex] will have a mass of [latex]\scriptsize 1~000~\text{kg.m}^{-3} \times 0.05~\text{m}^3 = 50~\text{kg}[/latex].
   2. The total mechanical energy (sum of gravitational potential energy and kinetic energy) in an isolated system remains constant as long as the system is free of friction and other non-conservative forces.
   3. .
      [latex]\scriptsize \begin{align*} a &= 9.8~\text{m.s}^{-1}\\ s &= 8~\text{m}\\ v_i &= 0~\text{m.s}^{-1}\\ v_f^2 &= v_i^2 + 2as\\ &= 2 \times 9.8~\text{m.s}^{-2} \times 8~\text{m}\\ &= 156.8~\text{m}^2\text{.s}^{-2}\\ \therefore v_f &= 12.52~\text{m.s}^{-1} \end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*} v &= 12.52~\text{m.s}^{-1}\\ m &= 50~\text{kg}\\ E_k &= \displaystyle \frac{1}{2}mv^2\\ &= \displaystyle \frac{1}{2} \times 50~\text{kg} \times (12.52~\text{m.s}^{-1})^2\\ &=3~918.76~\text{J} \end{align*}[/latex]
      .
      Because the water falls freely (without friction), we know that all the potential energy at the top of the pipe is converted into kinetic energy at the bottom of the pipe. Therefore, the total work done is [latex]\scriptsize 3~918.76~\text{J}[/latex].
      .
      This work is done every second. Therefore, the total power output is [latex]\scriptsize 3~918.76~\text{W}[/latex]. However, only [latex]\scriptsize 75\%[/latex] of this is converted to electrical power. Therefore, the electrical power output is [latex]\scriptsize 3~918.76~\text{W} \times 0.75 = 2~939.07~\text{W}[/latex].
2. .
   1. Power is the rate at which work is done.
   2. .
      [latex]\scriptsize \begin{align*} P &= 88~\text{kW} = 88~000~\text{W}\\ t &= 7~\text{minutes} = 420~\text{s}\\ P &= \displaystyle \frac{W}{t}&&\text{but work is equal to energy}\\ \therefore E &= P \times t\\ &= 88 000~\text{W} \times 420\\ &= 36.96 \times 10^6~\text{J} \end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*} m &= 3~000~\text{kg}\\ h &= 1~066~\text{m} – 366~\text{m} = 700~\text{m}\\ \Delta E_p &= mgh\\ &=3~000~\text{kg} \times 9.8~\text{m.s}^{-2} \times 700~\text{m}\\ &= 20.58 \times 10^6~\text{J} \end{align*}[/latex]
      .
      There is a difference of [latex]\scriptsize 36.96 \times 10^6~\text{J} - 20.58 \times 10^6~\text{J} = 16.38 \times 10^6~\text{J}[/latex]. The difference is due to energy ‘lost’ in overcoming friction and air resistance as well as the energy required to initially accelerate the car to its constant velocity.
   4. The total energy available is the car’s gravitational potential energy of [latex]\scriptsize 20.58 \times 10^6~\text{J}[/latex]. If [latex]\scriptsize 6 \times 10^6~\text{J}[/latex] is lost doing work against friction then the total energy available to be converted into kinetic energy is [latex]\scriptsize 14.58 \times 10^6~\text{J}[/latex].
      .
      [latex]\scriptsize \begin{align*} E &= \displaystyle \frac{1}{2} mv^2\\ \therefore v^2 &= \displaystyle \frac{2E}{m}\\ &=\displaystyle \frac{2 \times 14.58 \times 10^6~\text{J}}{3~000~\text{kg}}\\ \therefore v &= 98.59~\text{m.s}^{-1} \end{align*}[/latex]
      .
      This is equivalent to [latex]\scriptsize 355~\text{km/h}[/latex]
3. .
   1. Gravitational potential energy is the energy a body possesses owing to its position above a particular reference point (particularly the earth’s surface).
   2. .
      [latex]\scriptsize \begin{align*} m &= 6 \times 10^4~\text{kg}\\ h &= 948~\text{m}\\ E_p &= mgh\\ &= 6 \times 10^6~\text{kg} \times 9.8~\text{m.s}^{-2} \times 948~\text{m}\\ &= 5.574 x 10^8~\text{J} \end{align*}[/latex]
   3. As the water falls, its gravitational potential energy is converted into kinetic energy. Inside the turbine, the kinetic energy of the water is converted to mechanical energy of the turbine which is then converted to electrical energy.
      [latex]\scriptsize 6 \times 10^4~\text{kg}[/latex] of water falls from the top of the waterfall each minute. Therefore, the falling water can do [latex]\scriptsize 5.574 \times 10^8~\text{J}[/latex] every minute or [latex]\scriptsize 60~\text{s}[/latex]. However, only [latex]\scriptsize 80\%[/latex] of this is converted.
      [latex]\scriptsize \begin{align*} P &= \displaystyle \frac{W}{t} \times 80\%\\ &= \displaystyle \frac{5.574 \times 10^8~\text{J}}{60~\text{s}} \times 0.8\\ &= 7.432 \times 10^6~\text{W} \end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*} E_p &= E_k\\ m &= 1~\text{kg}\\ h &= 948~\text{m}\\ E_p &= 1~\text{kg} \times 9.8~\text{m.s}^{-2} \times 948~\text{m}\\ &= 9~290~\text{J} \end{align*}[/latex]
      .
      Therefore, the average kinetic energy would be [latex]\scriptsize 9~290~\text{J}[/latex].

Back to Unit 3: Assessment