Unit outcomes

By the end of this unit you will be able to:

• Define work and nett work.
• Calculate the amount of work done on an object when its displacement is either vertical or horizontal.

What you should know

Before you start this unit, make sure you can:

• Draw and use vector diagrams. Refer to level 3 subject outcome 2.2 unit 1 if you need help with this.
• Define energy and describe the different forms that energy can take. Refer to level 2 subject outcome 2.3 unit 1 if you need help with this.
• Describe and explain the concept of conservation of energy. Refer to level 2 subject outcome 2.3 unit 2 if you need help with this.
• Identify and determine the components of a force. Refer to level 3 subject outcome 2.2 unit 2 if you need help with this.
• Construct and interpret free-body diagrams. Refer to level 3 subject outcome 2.2 unit 3 if you need help with this.

Introduction

Think for a moment about the definition of ‘work’.

‘Work’ is a word we use often in everyday conversation. We go to work. We work at getting better at something. Some things are hard work! But in physics, the word ‘work’ has a very specific meaning.

In the previous subject outcome on momentum, we learnt that the momentum of a system is always conserved (the total energy in an isolated system is always constant). In elastic collisions, however, the kinetic energy of the system is also conserved – it is the same before and after the collision. In inelastic collisions, some of the kinetic energy of the system gets transformed into other kinds of energy.

In both cases, however, we have objects applying a force to other objects and transferring their energy. The greater the energy of the object, the greater the force it can apply. This is the basic idea of work. The more energy an object has, the more work it can do. If object A transfers some of its energy to object B, the energy of object A decreases by the same amount of energy that object B increases by, and object A has done work on object B.

What is work?

Work, in physics, is a measure of energy transfer that occurs when an object is moved over a distance by an external force. In other words, when a force acts upon an object to cause a displacement of the object, it is said that work was done upon the object. The three important ingredients are ‘force’, ‘displacement’ and ‘cause’. In order for a force to do work on an object, there must be a displacement and it must be the force that causes the displacement.

Can you think of at least three everyday occurrences where work is done? Stop and see if you can list them.

Here are some examples:

• a horse pulling a wagon
• a shopper pushing a shopping trolley
• a learner lifting a full bags of books onto their shoulder.

In each case there is a force exerted upon an object that causes that object to be displaced. In each case, the displacement is in the same direction as the nett applied force.

Take note!

Work is done when a force is exerted on an object that causes the object to be displaced (or moved). The direction of the displacement is in the same direction as the nett applied force.

Activity 1.1: Determine if work is being done

Time required: 10 minutes

What you need:

• a piece of paper
• a pen or pencil

What to do:

Think about the following situations. Is work being done? Write down whether work is done or not done in each case.

1. A weightlifter lifting a weight off the ground.
2. A weightlifter pushing a weight off his chest.
3. A weightlifter holding a weight stationary above his head.
4. Pushing against a wall.
5. A book falling off a table.
6. An aeroplane accelerating through the sky.
7. Pulling a box across a room.
8. A ball rolling down a hill.
9. A waiter carrying a tray across a room at a constant speed.

What did you find?

1. If a weightlifter lifts a weight off the ground, he is applying a force parallel with the direction of motion of the object and the object is moved over a certain distance, so work is done.
2. If a weightlifter pushes a weight off his chest, he is applying a force parallel with the direction of motion of the object and the object is moved over a certain distance, so work is done.
3. If a weightlifter holds a weight stationary over his head, there is no displacement and so no work is done. Even though he is exerting a force to counter-balance the force of gravity, because there is no displacement of the weight, no work is done.
4. If you push against a wall, you certainly exert a force against the wall and the wall exerts a force against you. However, neither the wall nor you move over a distance and so no work is done.
5. If a book falls off a table, the force of gravity acts in the direction of the motion of the book and the book is moved over a certain distance, so work is done. Even through the velocity of the book is not constant during the fall, the force being applied is constant.
6. If an aeroplane accelerates through the sky, the force parallel to the motion of the aircraft is applied to it and it moves over a certain distance, so work is done.
7. If a box is pulled across a room, there is a force parallel to the direction of motion of the box and the box moves over a distance and so work is done.
8. When a ball rolls down a hill, there is a component of the force of gravity acting in parallel to the motion of the ball and the ball moves over a distance, therefore, work is done.
9. There is a force on the tray, but this is upwards to counteract the force of gravity. There is a displacement of the tray as it moves across the room. However, the force does not cause the displacement. There is no component of the lifting force in the direction of the displacement and so the force is not causing the displacement. Therefore, no work is done.

Scenario 9 in activity 1.1 was a tricky one which we will explore in more detail later. For now, it is important to remember that for work to be done, the force or at least a component of the force, must be in the direction of the displacement.

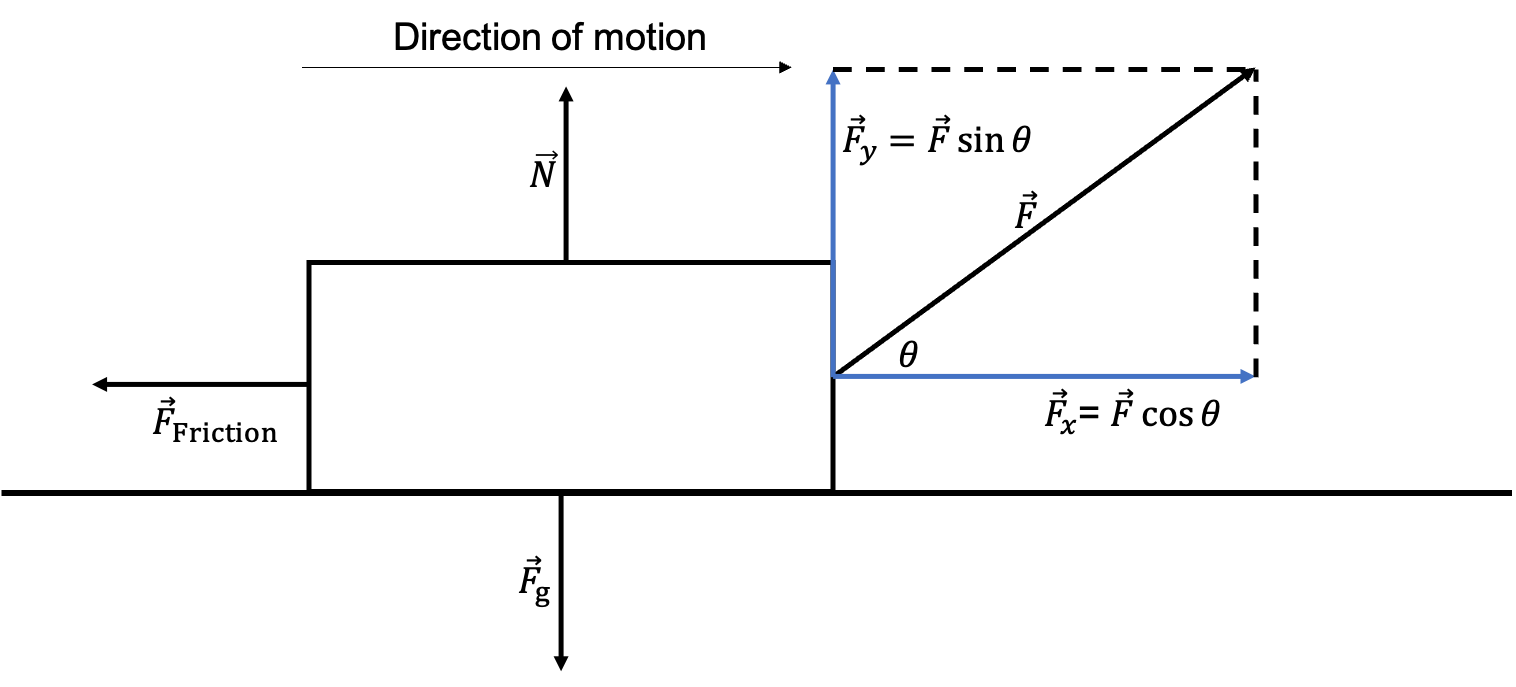
The work done can be expressed mathematically as [latex]\scriptsize W = F \Delta x \cos \theta[/latex] where:

• [latex]\scriptsize W[/latex] is the work done (measured in newton metres or joules – [latex]\scriptsize 1~\text{N.m} = 1~\text{J}[/latex])
• [latex]\scriptsize F[/latex] is the force acting on the object (measured in newtons)
• [latex]\scriptsize \Delta x[/latex] is the displacement (measured in metres) – note that [latex]\scriptsize \Delta x[/latex] can also be represented as [latex]\scriptsize d[/latex]
• [latex]\scriptsize \theta[/latex] is the angle between the force and the displacement vector (hence [latex]\scriptsize \cos \theta[/latex] gives us the component of the force that acts in parallel with the displacement (see figure 1).

If the force is parallel to the direction of motion, and in the same direction, then [latex]\scriptsize \theta = 0^\circ[/latex], [latex]\scriptsize \cos \theta = 1[/latex] and [latex]\scriptsize W = F \Delta x \cos \theta[/latex] becomes simply [latex]\scriptsize W = F \Delta x[/latex] (see figures 2 and 3).

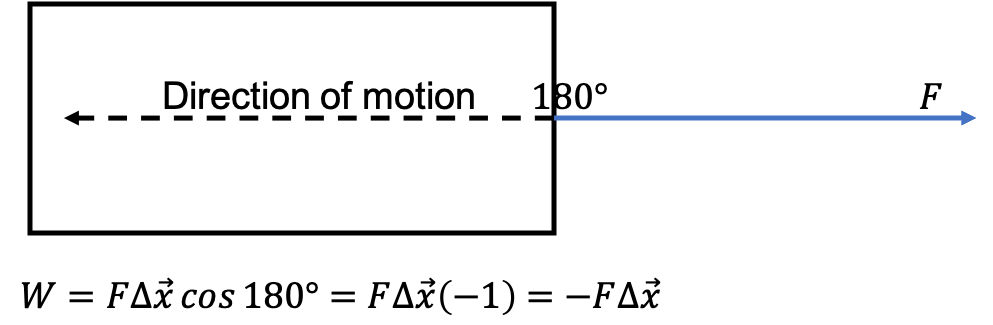
If the force is parallel to the direction of motion, but in the opposite direction, then [latex]\scriptsize \theta = 180^\circ[/latex], [latex]\scriptsize \cos \theta = -1[/latex] and [latex]\scriptsize W = F \Delta x \cos \theta[/latex] become [latex]\scriptsize W = F \Delta x (-1)[/latex] (see figure 4). We get a negative value for work. It is important to note that work is not a vector and so only has a magnitude. If negative work is done, energy is lost (rather than gained) and the object exerting the force gains this energy. For example, if you try to push a car uphill by applying a force up the slope and instead the car rolls down the hill, you are doing negative work on the car. Another way of saying this is that the car is doing positive work on you.

If the force and the direction of displacement are perpendicular, then [latex]\scriptsize \theta = 90^\circ[/latex], [latex]\scriptsize \cos \theta = 0[/latex] and [latex]\scriptsize W = F \Delta x \cos \theta[/latex] become [latex]\scriptsize W = F \Delta x (0) = 0[/latex]. Therefore, no work is done.

Before we move on, let’s examine scenario 9 of the waiter carrying the tray from activity 1.1 in more detail. If the waiter and tray started at rest, there would be a brief period of time when the waiter would have had to apply a force to the tray to get it to start moving (i.e. to accelerate it). However, once the tray is at its constant speed, it will stay in its straight-line motion at this constant speed without a forward force. If the only force exerted upon the tray during this constant speed stage of its motion is upward, then no work is done on the tray during this period. Remember, a vertical force does not do work on a horizontally displaced object.

Take note!

When a force or a component of a force acts in the direction of motion of an object to cause the object’s displacement, work is done on the object. The work done on an object by a constant force [latex]\scriptsize F[/latex] is:
[latex]\scriptsize W = F \Delta x \cos \theta[/latex]
Where:

• [latex]\scriptsize F[/latex] is the magnitude of the force
• [latex]\scriptsize \Delta x[/latex] is the magnitude of the displacement
• [latex]\scriptsize \theta[/latex] is the angle between the force and the displacement.

If the force is perfectly parallel to the direction of motion and in the same direction, then [latex]\scriptsize \theta = 0^\circ[/latex] and so [latex]\scriptsize \cos \theta = \cos 0^\circ = 1[/latex] and [latex]\scriptsize W = F \Delta x \times 1= F \Delta x[/latex].

If the force is perfectly parallel but in the opposite direction to the direction of motion, then [latex]\scriptsize \theta = 180^\circ[/latex] and so [latex]\scriptsize \cos \theta = \cos 180^\circ = -1[/latex] and [latex]\scriptsize W = F \Delta x \times (-1) = -F \Delta x[/latex].

If the force and the direction of displacement are perpendicular then [latex]\scriptsize \theta = 90^\circ[/latex] and so [latex]\scriptsize \cos \theta = 0[/latex] and [latex]\scriptsize W = F \Delta x \cos \theta = F \Delta x \times 0 = 0[/latex].

We will only deal with occasions where [latex]\scriptsize \theta = 0^\circ[/latex] or [latex]\scriptsize \theta = 180^\circ[/latex].

Example 1.1

A bicycle is travelling along a straight horizontal road. The cyclist applies a force of [latex]\scriptsize 50~\text{N}[/latex] through the pedals and chain in the direction in which she is travelling, and is speeding up. While she is accelerating, she covers a distance of [latex]\scriptsize 65~\text{m}[/latex]. Calculate the work done by the cyclist.

Solution

[latex]\scriptsize \begin{align*} F &= 50~\text{N}\\ \Delta x &= 65~\text{m}\\ \theta &= 0^\circ &&\text{the applied force of }50~\text{N is in the direction of travel} \end{align*}[/latex]

We need to calculate the work done.
[latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &=50~\text{N} \times 65~\text{m} \times \cos 0^\circ\\ &= 50~\text{N} \times 65~\text{m} \times 1\\ &= 3~250~\text{N.m} \end{align*}[/latex]

[latex]\scriptsize 3~250~\text{N.m}[/latex] or [latex]\scriptsize 3~250~\text{J}[/latex] of work is done. This means that the energy of the bicycle (and rider) increased.

Example 1.2

The same cyclist as above applies her brakes to slow down. The force applied by the brakes opposite to her direction of travel is [latex]\scriptsize 45~\text{N}[/latex] and she travels [latex]\scriptsize 50~\text{m}[/latex] while braking. Calculate the work done by the brakes.

Solution

[latex]\scriptsize \begin{align*} F &= 45~\text{N}\\ \Delta x &= 50~\text{m}\\ \theta &= 180^\circ &&\text{the applied force of }45~\text{N is in the opposite direction to the direction of travel} \end{align*}[/latex]

We need to calculate the work done.
[latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 45~\text{N} \times 50~\text{m} \times \cos 180^\circ\\ &= 45~\text{N} \times 50~\text{m} \times (-1)\\ &= -2~250~\text{N.m} \end{align*}[/latex]

[latex]\scriptsize –2~250~\text{N.m}[/latex] or [latex]\scriptsize -2~250~\text{J}[/latex] of work is done. This means that that energy of the bicycle (and rider) decreased.

Nett work

Hardly ever is there only a single force acting on an object. In activity 1.2, we will investigate some simple cases of this.

Activity 1.2: Determine how much work is being done

Time required: 15 minutes

What you need:

• a pen or pencil
• a piece of paper

What to do:

Study the following free-body diagrams and determine which forces are doing work and how much work these forces are doing. Then determine the overall work being done.

1. A [latex]\scriptsize 15~\text{N}[/latex] force is applied to push a block across a frictionless surface for a displacement of [latex]\scriptsize 10.0~\text{m}[/latex] to the right.
   
2. A [latex]\scriptsize 15~\text{N}[/latex] frictional force slows a block moving to the right to a stop after a displacement of [latex]\scriptsize 10.0~\text{m}[/latex].
   
3. A [latex]\scriptsize 15~\text{N}[/latex] force is applied to push a block across a frictional surface at a constant speed for a displacement of [latex]\scriptsize 10.0~\text{m}[/latex] to the right.
   
4. A [latex]\scriptsize 3.06~\text{kg}[/latex] object is sliding at constant speed across a frictionless surface for a displacement of [latex]\scriptsize 10~\text{m}[/latex] to the right.
   
5. A [latex]\scriptsize 3~\text{kg}[/latex] object is pulled vertically upward by a [latex]\scriptsize 29.4~\text{N}[/latex] force at a constant speed for a vertical displacement of [latex]\scriptsize 10~\text{m}[/latex] up.
   

What did you find?

1. The gravitational and normal forces act perpendicular to the displacement. Therefore, they do no work. The applied force acts parallel to the displacement; therefore, it does work. The work done by this force is [latex]\scriptsize W = F \Delta x \cos \theta = 15~\text{N} \times 10~\text{m} \times cos 0^\circ = 150~\text{J}[/latex]. This is the only force doing work, so the nett work is [latex]\scriptsize 150~\text{J}[/latex].
2. The gravitational and normal forces act perpendicular to the displacement. Therefore, they do no work. The frictional force acts parallel (but in the opposite direction) to the displacement; therefore, it does work. The work done by this force is [latex]\scriptsize W = F \Delta x \cos \theta = 15~\text{N} \times 10~\text{m} \times \cos 180^\circ = -150~\text{J}[/latex]. This is the only force doing work, so the nett work is [latex]\scriptsize -150~\text{J}[/latex].
3. The gravitational and normal forces act perpendicular to the displacement. Therefore, they do no work. The applied force acts parallel to the displacement; therefore, it does work. The work done by this force is [latex]\scriptsize W = F \Delta x \cos \theta = 15~\text{N} \times 10~\text{m} \times \cos 0^\circ = 150~\text{J}[/latex]. The frictional force acts parallel (but in the opposite direction) to the displacement; therefore, it does work too. The work done by this force is [latex]\scriptsize W = F \Delta x \cos \theta = 15~\text{N} \times 10~\text{m} \times \cos 180^\circ = -150~\text{J}[/latex]. Therefore, the nett work is [latex]\scriptsize 150~\text{J} + (-150~\text{J}) = 0~\text{J}[/latex]. In other words, no nett work is done. This is a very important result!
4. The gravitational and normal forces act perpendicular to the displacement. Therefore, they do no work. There is no force (or component of a force) acting in parallel to the displacement. Therefore, no work is done.
5. The gravitational and normal forces act parallel to the displacement. Therefore, they do work. The work done by the upward tension force is [latex]\scriptsize W = F \Delta x \cos \theta = 29.4~\text{N} \times 10~\text{m} \times \cos 0^\circ = 294~\text{J}[/latex]. The gravitational force acts parallel (but in the opposite direction) to the displacement; therefore, it does work. The work done by this force is [latex]\scriptsize W = F \Delta x \cos \theta = 15~\text{N} \times 10~\text{m} \times \cos 180^\circ = 3~\text{kg} \times 9.8~\text{m.s}^{-2} \times 10~\text{m} \times (-1) = -294~\text{J}[/latex]. Therefore, the nett work is [latex]\scriptsize 294~\text{J} + (-294~\text{J}) = 0~\text{J}[/latex]. In other words, no nett work is done.

Example 1.3

How much work is done by an applied force to lift a [latex]\scriptsize 15~\text{kg}[/latex] block [latex]\scriptsize 12.0~\text{m}[/latex] vertically at a constant speed?

Solution

Firstly, if the block is lifted at a constant velocity, this means that there is no acceleration. Therefore, the force lifting the block will be equal but opposite to the force of gravity. The applied force must, therefore, be equal to the weight of the block.

[latex]\scriptsize \begin{align*} m &= 15~\text{kg}\\ g &= 9.8~\text{m.s}^{-2}\\ h &= 12.0~\text{m} \end{align*}[/latex]

[latex]\scriptsize F = mg = 15~\text{kg} \times 9.8~\text{m.s}^{-2}= 147~\text{N}[/latex]

[latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ \text{But } \Delta x &= h \text { and } \theta = 0^\circ\\ \therefore W &= F \times h\\ &= 147~\text{N} \times 12~\text{m}\\ &= 1~764~\text{J} \end{align*}[/latex]

Example 1.4

A force of [latex]\scriptsize 500~\text{N}[/latex] is accelerating a car down a flat straight road. Friction is working against the motion of the car. A frictional force of [latex]\scriptsize 350~\text{N}[/latex] acts to oppose the motion. Calculate the nett work done on the car to move it forward [latex]\scriptsize 50~\text{m}[/latex].

Solution

The applied force is [latex]\scriptsize 500~\text{N}[/latex] and the frictional force is [latex]\scriptsize 350~\text{N}[/latex] acting in the opposite direction to the car’s motion. There is no work done by gravity or the normal force because these are perpendicular to the car’s motion. The road is flat.

[latex]\scriptsize \begin{align*} F_{applied} &= 500~\text{N}\\ F_{fric} &= 350~\text{N}\\ \Delta x &= 50~\text{m} \end{align*}[/latex]

[latex]\scriptsize \begin{align*} W_{applied} &= F \Delta x \cos \theta\\ &=500~\text{N} \times 50~\text{m} \times \cos 0^\circ\\ &= 25~000~\text{J} \end{align*}[/latex]

[latex]\scriptsize \begin{align*} W_{friction} &= F \Delta x \cos \theta\\ &= 350~\text{N} \times 50~\text{m} \times \cos 180^\circ\\ &= -17~500~\text{J} \end{align*}[/latex]

[latex]\scriptsize \begin{align*} W_{net} &= W_{applied} + W_{friction}\\ &=25~000~\text{J} – 17~500~\text{J}\\ &= 7~500~\text{J} \end{align*}[/latex]

Alternatively, we can calculate the total work by first calculating the nett force on the car.
Define forward as positive
[latex]\scriptsize \begin{align*} F_{applied} &= 500~\text{N}\\ F_{friction} &= -350~\text{N} \end{align*}[/latex]

Both forces act in the same horizontal plane so the vector addition is simple and does not require calculating any horizontal components.
[latex]\scriptsize F_{nett} = F_{applied} + F_{friction} = 500~\text{N} – 350~\text{N} = 150~\text{N}[/latex]

Neither gravitational force nor the normal force have horizontal components – they act perpendicular to the motion.

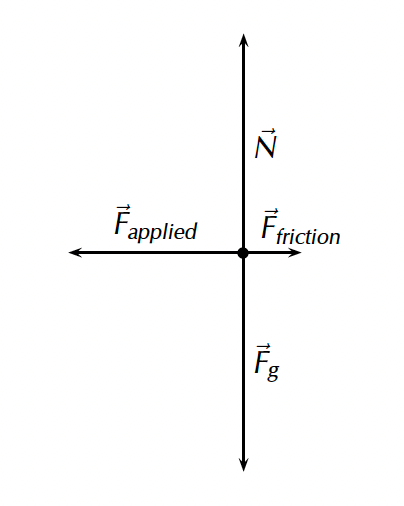
[latex]\scriptsize \begin{align*} W_{nett} &= F_{nett} \Delta x \cos \theta\\ &=150~\text{N} \times 50~\text{m} \times \cos 0^\circ\\ &= 7~500~\text~\text{J} \end{align*}[/latex]

Exercise 1.1

1. A traveller carries a [latex]\scriptsize 250~\text{N}[/latex] suitcase up four flights of stairs (a total height of [latex]\scriptsize 10.5~\text{m}[/latex]) and then pushes it with a horizontal force of [latex]\scriptsize 50~\text{N}[/latex] at a constant speed of [latex]\scriptsize 0.25~\text{m.s}^{-1}[/latex] for a horizontal distance of [latex]\scriptsize 50~\text{m}[/latex] on a frictionless surface. How much work does the traveller do on the suitcase during this entire trip?
2. How much work is done by the force required to raise a [latex]\scriptsize 3~000~\text{N}[/latex] lift five floors vertically at a constant speed? The vertical distance between floors is [latex]\scriptsize 5~\text{m}[/latex] high.
3. A learner with a mass of [latex]\scriptsize 60~\text{kg}[/latex] runs up three flights of stairs in [latex]\scriptsize 15~\text{s}[/latex], covering a vertical distance of [latex]\scriptsize 10~\text{m}[/latex]. Determine the amount of work done by the learner to elevate her body to this height if her speed was constant.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• Work is done on an object when a force acts on an object to cause a displacement of the object.
• Work is expressed mathematically as [latex]\scriptsize W = F \Delta x \cos \theta[/latex] where [latex]\scriptsize \theta[/latex] is the angle between the force and the displacement vector.
• Nett work is the work done by the nett force acting on an object that causes a displacement of the object.

Unit 1: Assessment

Suggested time to complete: 30 minutes

1. Before beginning its initial descent, a roller coaster car is pulled up the first hill to a high initial height. Work is done on the car to achieve this initial height. A roller coaster designer is considering three different incline angles at which to drag the [latex]\scriptsize 2~500~\text{kg}[/latex] car to the top of a [latex]\scriptsize 70~\text{m}[/latex] high hill. In each case, the force applied to the car will be applied parallel to the hill. Which of the following options would require the most work?
   

   Option	Angle	Force	Distance
   A	[latex]\scriptsize 35^\circ[/latex]	[latex]\scriptsize 1.12 \times 10^{4}~\text{N}[/latex]	[latex]\scriptsize 105~\text{m}[/latex]
   B	[latex]\scriptsize 45^\circ[/latex]	[latex]\scriptsize 1.39 \times 10^{4}~\text{N}[/latex]	[latex]\scriptsize 84.60~\text{m}[/latex]
   C	[latex]\scriptsize 55^\circ[/latex]	[latex]\scriptsize 1.61 \times 10^{4}~\text{N}[/latex]	[latex]\scriptsize 73.04~\text{m}[/latex]

2. A [latex]\scriptsize 120~\text{kg}[/latex] rugby player does push-ups by applying a force to elevate his centre-of-mass by [latex]\scriptsize 30~\text{cm}[/latex]. Calculate the number of push-ups that he needs to do to do at least [latex]\scriptsize 10~000~\text{J}[/latex] of work. Assume no air resistance.
3. Car A and car B both have a mass of [latex]\scriptsize 950~\text{kg}[/latex]. Car A can accelerate from rest to [latex]\scriptsize 100~\text{km/h}[/latex] in [latex]\scriptsize 16~\text{s}[/latex]. Car B can accelerate from rest to [latex]\scriptsize 100~\text{km/h}[/latex] in [latex]\scriptsize 3.5~\text{s}[/latex].
   1. To accelerate to [latex]\scriptsize 100~\text{km/h}[/latex], which engine will do more work. Justify your answer with calculations. Assume that both cars accelerate in a straight line. Ignore the effects of air resistance and friction.
   2. What is this work?

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. Work done up the steps:
   [latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 250~\text{N} \times 10.5~\text{m} \times \cos 0^\circ\\ &= 2~625~\text{J} \end{align*}[/latex]
   .
   Work done pushing:
   [latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 50~\text{N} \times 50~\text{m} \times \cos 0^\circ\\ &= 2~500~\text{J} \end{align*}[/latex]
   .
   [latex]\scriptsize \text{Total work} = 2~625~\text{J} + 2~500~\text{J} = 5~125~\text{J}[/latex]
2. .
   [latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 3~0000~\text{N} \times (5\times 5)~\text{m}\\ &= 75~000~\text{J} \end{align*}[/latex]
3. As speed is constant, the learner is only doing work enough to equal the force of gravity.
   [latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 60~\text{kg} \times 9.8~\text{m.s}^{-2} \times 10~\text{m} \times \cos 0^\circ\\ &= 5~880~\text{J} \end{align*}[/latex]

Back to Exercise 1.1

Unit 1: Assessment

1. The angle in the table is the incline angle. The angle [latex]\scriptsize \theta[/latex] in the work equation is the angle between [latex]\scriptsize F[/latex] and [latex]\scriptsize \Delta x[/latex]. If the force is parallel to the incline and the direction of the displacement is parallel to the incline, then the angle [latex]\scriptsize \theta[/latex] in the work equation is [latex]\scriptsize 0^\circ[/latex]. For this reason, [latex]\scriptsize W = F \Delta x \cos 0^\circ = F \Delta x[/latex].
   .
   [latex]\scriptsize W = F \Delta x \cos \theta[/latex]
   A: [latex]\scriptsize 35^\circ[/latex]: [latex]\scriptsize W = 1.12 \times 10^4~\text{N} \times 105~\text{m} = 1~176~000~\text{J}[/latex]
   B: [latex]\scriptsize 45^\circ[/latex]: [latex]\scriptsize W = 1.39 \times 10^4~\text{N} \times 84.60~\text{m} = 1~175~940~\text{J}[/latex]
   C: [latex]\scriptsize 55^\circ[/latex]: [latex]\scriptsize W = 1.61 \times 10^4~\text{N} \times 73.04~\text{m} = 1~175~944~\text{J}[/latex]
   .
   While there are small differences in the work done, given the amount of work these can largely be put down to rounding errors. It really does not make much difference which option is used. The total work required to get the car to the top will be about the same (about [latex]\scriptsize 1~176~000~\text{J}[/latex])
2. Each push up requires the player to do work only against gravity to lift his body.
   [latex]\scriptsize \begin{align*} W &= F \Delta x \cos \theta\\ &= 120~\text{kg} \times 9.8~\text{m.s}^{-2} \times 0.3~\text{m}\\ &= 352.8~\text{J} \end{align*}[/latex]
   .
   [latex]\scriptsize \displaystyle \frac{10~000~\text{J}}{352.8~\text{J}} = 28.34[/latex]
   .
   Therefore, the player will need to do at least [latex]\scriptsize 29[/latex] push-ups to do [latex]\scriptsize 10~000~\text{J}[/latex] of work.
3. .
   1. In both cases, the force accelerating the cars is parallel and in the same direction to the displacement. Therefore, [latex]\scriptsize \theta = 0^\circ[/latex] and [latex]\scriptsize \cos \theta = 1[/latex].
      .
      [latex]\scriptsize \begin{align*} W &= F \Delta x\\ \text{But }F &= ma\\ \therefore W &= ma \Delta x\\ \text{But }a &= \displaystyle \frac{v_f - v_i}{t}\\ \therefore W &= \displaystyle \frac{m (vf - vi)}{t} \Delta x\\ \text{But } \Delta x &= s = \displaystyle \frac{1}{2} (v_i + v_f)t\\ \therefore W &= \displaystyle \frac{m (v_f - v_i)}{t} \times \displaystyle \frac{1}{2} (v_i + v_f) t\\ &= \displaystyle \frac{1}{2} m (v_f - v_i)(v_i + v_f) \end{align*}[/latex]
      .
      Therefore, as both cars have the same mass, the same initial velocity and the same final velocity, both engines will need to do the same amount of work.
   2. .
      [latex]\scriptsize \begin{align*} m &= 950~\text{kg}\\ v_i &= 0~\text{m.s}^{-1}\\ v_f &= 100~\text{km/h} = 27.78~\text{m.s}^{-1}\\ W &= \displaystyle \frac{1}{2}m (v_f – v_i)(v_i + v_f)\\ &= \displaystyle \frac{1}{2} m (v_f)(v_f)\\ &= \displaystyle \frac{1}{2} m(v_f)^2\\ &= \displaystyle \frac{1}{2}\times 950~\text{kg} \times (27.78~\text{m.s}^{-1})^2\\ &= 366~570.99~\text{J} \end{align*}[/latex]
      .
      Notice how the total work done by the engines is equal to the change in kinetic energy. We will investigate this idea in more detail in unit 2.
      .
      Refer back to Refer to level 2 subject outcome 2.1 if you need to on how to determine acceleration.

Back to Unit 1: Assessment