Unit outcomes

By the end of this unit you will be able to:

• Define and identify conservative forces.
• Define and identify non-conservative forces.
• State and apply the work-energy theorem.

What you should know

Before you start this unit, make sure you can

• Define and calculate work. Refer to unit 1 if you need help with this.
• Define mechanical energy.
• Define kinetic energy.
• Define gravitational potential energy.
• Calculate kinetic energy ([latex]\scriptsize E_k = \displaystyle \frac{1}{2}mv^2[/latex]).
• Calculate gravitational potential energy ([latex]\scriptsize E_p=mgh[/latex]).
• Refer to level 2 subject outcome 2.3 if you need help with any of these other concepts.

Introduction

In level 2 subject outcome 2.3, we learnt that an object has potential energy due to its position above the earth or its position in earth’s field of gravity. This is gravitational potential energy. If you let go of the object, it will fall, and it can do work on your toe! We also learnt that the amount of this gravitational potential energy is proportional to the mass of the object and its height. The heavier the object is or the greater the height the object falls from, the more work it can do on your toe.

We calculate gravitational potential energy as [latex]\scriptsize E_p = mgh[/latex].

Note that another form of potential energy is elastic potential energy. This is the energy stored in a compressed spring or a stretched elastic.

We also learnt that an object has energy due to its motion, more specifically, its velocity. This is kinetic energy. The faster an object is moving, the more energy it has and the more work it can do on other objects. We also learnt that the amount of kinetic energy is proportional to the object’s mass and the square of its velocity.

We calculate kinetic energy as [latex]\scriptsize E_k = \displaystyle \frac{1}{2}mv^2[/latex].

The mechanical energy of an object is simply the sum of its potential energy and kinetic energy and is, therefore, a measure of the total amount of work that the object can do.

We calculate mechanical energy as [latex]\scriptsize E_{mechanical} = E_p + E_k[/latex].

Work and energy

We know from level 2 subject outcome 2.3 that mechanical energy is conserved in a closed system. In other words, if you drop a ball from a height, all the ball’s gravitational potential energy at this height is converted to kinetic energy when it hits the ground. In other words, in figure 1, the ball’s mechanical energy at point A is equal to the ball’s mechanical energy at point B. At point A, the ball’s mechanical energy is all gravitational potential energy. At point B it has all been converted into kinetic energy.

But is this always the case? Is mechanical energy always conserved? Think of a car travelling on a flat road. What happens to its mechanical energy if the engine stops?

Our experience tells us that the car’s mechanical energy is not conserved. It will eventually roll to a stop. In this case, its gravitational potential energy is not changing (it is on a flat road) but its kinetic energy certainly is. We know why the car eventually stops and loses all its mechanical energy. Forces like friction and the rolling resistance of the tyres on the ground always exert a force in the opposite direction to the car’s motion.

Mechanical energy is only conserved when all the forces acting on an object are conservative forces. Examples of conservative forces include gravity and spring forces. They are called conservative forces precisely because they result in the conservation of mechanical energy as illustrated in figure 1.

If non-conservative forces act on the object, then its total mechanical energy will change. Non-conservative forces, as the name suggests, do not result in the conservation of mechanical energy. Examples include friction, air resistance, rolling resistance, any applied force and tension forces.

If a body is acted on by non-conservative forces, its mechanical energy will either increase or decrease. If positive work is done, then the object will gain energy. If negative work is done, then the object will lose energy. This gain or loss in energy can be in the form of potential energy, kinetic energy, or both.

Take note!

Conservative forces result in the conservation of mechanical energy. The object’s energy simply changes form from kinetic to potential or vice versa. Conservation forces are sometimes called internal forces. The work done by a conservative force only depends on the starting and ending points of the motion not the path taken.

Non-conservative forces result in the change of mechanical energy. The object gains or loses mechanical energy. Non-conservative forces are sometimes called external forces. The work done by non-conservative forces depends on the path taken.

Activity 2.1: Mechanical energy is conserved

Time required: 10 minutes

What you need:

• a pen or pencil
• a piece of paper

What to do:

Study the following simple scenarios, and in each case:

• identify what kinds of forces are involved in doing the work
• identify whether mechanical energy is being conserved or not
• if mechanical energy is conserved, state whether it is being from kinetic energy to potential energy or vice versa
• if mechanical energy is not conserved, state whether there is a change in the kinetic energy, potential energy or both.

1. A ball falls from a height of 3 m in the absence of air resistance.
2. A stationary ball just after it is kicked along the ground.
3. A skier glides from one point to another down an undulating friction-free icy slope.
4. A cricket ball is traveling vertically upwards.
5. A horizontally moving hammer just after it strikes a nail into a block of wood.
6. The end of a compressed spring as it is released.

What did you find?

1. The only force doing work on the ball is gravity. Therefore, mechanical energy is conserved. As the ball loses height it gains velocity. Potential energy is converted into kinetic energy.
2. The applied force of the foot causes the ball to accelerate and hence gain kinetic energy. As there is no change in the potential energy of the ball, the ball gains mechanical energy. Thus, a non-conservative applied force changes the kinetic energy of the ball.
3. The only force doing work on the skier is gravity. Therefore, mechanical energy is conserved. As the skier loses height on the downhills, she gains velocity. As she loses velocity on the uphills, she gains height. Potential energy is converted into kinetic energy and vice versa but as her initial height is greater than her final height, the overall conversion is from potential energy to kinetic energy.
4. The only force doing work on the ball is gravity. Therefore, mechanical energy is conserved. As the ball gains height, it loses velocity. Kinetic energy is converted into potential energy.
5. The hammer is moving horizontally so there is no change in potential energy. The equal and opposite force of the nail acting on the hammer causes the hammer to stop or gain negative velocity. Therefore, there is a change in the hammer’s kinetic energy and its mechanical energy is not conserved.
6. The only force doing work on the end of the spring is the compression force of the spring. The spring changes from a compressed state to a relaxed state changing the velocity of the end of the spring. Thus, the conservative potential spring energy is transformed into kinetic energy.

Take note!

That mechanical energy is not conserved when non-conservative forces act on an object does not mean that total energy is not conserved. Total energy is always conserved. Non-conservative forces simply mean that mechanical energy is not conserved in a particular system which implies that some energy is transferred in a process that isn’t reversible, such as losses to heat.

The work-energy theorem

Consider the simple case of sliding a box across the floor (see figure 2). There is an applied force pulling the box to the right and a frictional force acting in the opposite direction. We will define to the right as positive.

• If [latex]\scriptsize F_{applied} \gt F_{friction}[/latex], there is a nett force to the right. The box will accelerate to the right. It will gain velocity. Nett positive work will be done on the box.
• If [latex]\scriptsize F_{applied} \lt F_{friction}[/latex], there is a nett force to the left. The box will accelerate to the left (its acceleration will be negative). It will lose velocity. Nett negative work will be done on the box.
• If [latex]\scriptsize F_{applied} = F_{friction}[/latex], there is no nett force. The box will experience no acceleration. There will be no change in its velocity. If it is stationary, it will remain stationary. If it is moving it will remain moving in this direction at a constant velocity. No nett work will be done on the box. This does not mean that the applied force and the frictional force are not individually doing work, just that the nett work on the box will be zero.

Now consider the simple case of a box being lifted into the air (see figure 3). There is an applied force lifting the box up and a gravitational force acting in the opposite direction. We

• If [latex]\scriptsize F_{applied} \gt F_{gravity}[/latex], there is a nett force up. The box will accelerate up. It will gain velocity. Nett positive work will be done on the box.
• If [latex]\scriptsize F_{applied} \lt F_{gravity}[/latex], there is a nett force down. The box will accelerate down (its acceleration will be negative). It will lose velocity. Nett negative work will be done on the box.
• If [latex]\scriptsize F_{applied} = F_{gravity}[/latex], there is no nett force. The box will experience no acceleration. There will be no change in its velocity. If it is stationary, it will remain stationary. If it is moving it will remain moving in this direction at a constant velocity. No nett work will be done on the box. This does not mean that the applied force and the gravitational force are not individually doing work, just that the nett work on the box will be zero.

This leads us to the conclusion that when a nett force does work on an object, then there is always a change in the kinetic energy of the object. This is because the object experiences an acceleration and therefore a change in velocity.

This leads to the work-energy theorem.

To understand what this means in practice, it is helpful to look at some examples.

Example 2.1

Question adapted from Everything Science Grade 12 Worked example 6 page 232

A [latex]\scriptsize 2~\text{kg}[/latex] brick is dropped from a height of [latex]\scriptsize 15~\text{m}[/latex]. Calculate the work that has been done on the brick between the moment it is released and the moment when it hits the ground. Assume that air resistance can be neglected.

Solution

The brick falls freely with only conservative forces acting on it, so energy is conserved. We know that the work done is equal to the brick’s change in kinetic energy. The brick has no kinetic energy at the moment it is dropped, because it is stationary. When the brick hits the ground, all the brick’s potential energy is converted to kinetic energy.

[latex]\scriptsize \begin{align*} m &= 2~\text{kg}\\ h &= 15~\text{m}\\ E_P &= mgh\\ &= 2~\text{kg} \times 9.8~\text{m.s}^{-2} \times 15~\text{m}\\ &= 294~\text{J} \end{align*}[/latex]

But the brick had [latex]\scriptsize 294~\text{J}[/latex] of potential energy when it was released and [latex]\scriptsize 0~\text{J}[/latex] of kinetic energy.

When the brick hits the ground, it has [latex]\scriptsize 0~\text{J}[/latex] of potential energy and [latex]\scriptsize 294~\text{J}[/latex] of kinetic energy.

Therefore [latex]\scriptsize E_{ki} = 0~\text{J}[/latex] and [latex]\scriptsize E_{kf} = 294~\text{J}[/latex].

[latex]\scriptsize \begin{align*} W_{nett} &= \Delta E_k = E_{kf} – E_{ki}\\ &= 294~\text{J} – 0~\text{J}\\ &= 294~\text{J} \end{align*}[/latex]

Example 2.2

A [latex]\scriptsize 980~\text{kg}[/latex] car traveling on a flat road skids to a stop from an initial velocity of [latex]\scriptsize 27~\text{m.s}^{-1}[/latex]. The car’s brakes apply a [latex]\scriptsize 7~650~\text{N}[/latex] of frictional force. What is the stopping distance of the car?

Solution

There is no change in the potential energy of the car. Therefore, we can ignore any change in potential energy. We will define the direction of the car’s initial motion as positive.

[latex]\scriptsize \begin{align*} m &= 980~\text{kg}\\ v_i &= 27~\text{m/s}^{-1}\\ v_f &= 0~\text{m/s}^{-1}\\ F_{nett} &= 7~650~\text{N}\\ E_{Ki} &= \displaystyle \frac{1}{2}mv^2\\ &= \displaystyle \frac{1}{2} 980~\text{kg} \times (27~\text{m.s}^{-1})^2\\ &= 357~210~\text{J} \end{align*}[/latex]

[latex]\scriptsize E_{Kf} = 0~\text{J}[/latex]

[latex]\scriptsize \begin{align*} W_{nett} &= \Delta E_k = E_{kf} – E_{ki}\\ \therefore W_{nett} &= 0~\text{J} – 357 210~\text{J}\\ &= -357~210~\text{J} &&\text{note that nett work is negative i.e. the car loses mechanical energy} \end{align*}[/latex]

[latex]\scriptsize \begin{align*} W_{nett} &= F_{nett} \Delta x \cos \theta\\ \therefore \Delta x &=\displaystyle \frac{W_{nett}}{F_{nett}} \times \cos \theta\\ &= \displaystyle \frac{-357~210~\text{J}}{7~650~\text{N}} \times \cos 180^\circ &&\text{remember that J = N.m so } \displaystyle \frac{\text{J}}{\text{N}}=\displaystyle \frac{\text{N.m}}{\text{N}}=\text{m}\\ &= 46.69~\text{m}\\ \end{align*}[/latex]

The car will stop in [latex]\scriptsize 46.69~\text{m}[/latex].

We can use the work-energy theorem to generate an expression to calculate the total work done by all the non-conservative forces in a system.

We know that [latex]\scriptsize F_{nett} = F_{conservative} + F_{non-conservative}[/latex] (the nett work done is the sum of the work done by all of the individual forces).

Therefore, [latex]\scriptsize W_{nett} = W_{conservative} +W_{non-conservative}[/latex].

But the work-energy theorem tells us that [latex]\scriptsize W_{nett} = \Delta E_K[/latex]. Therefore, [latex]\scriptsize \Delta E_K = W_{conservative} +W_{non-conservative}[/latex].

But the work done by conservative forces can be expressed as [latex]\scriptsize \Delta PE[/latex]. Remember, if you lift an object at a constant velocity, the conservative force (gravitational force) acts in the opposite direction to the motion (negative work) but its magnitude is equal to the gain in potential energy of the object.

Therefore, [latex]\scriptsize \Delta E_K = -\Delta E_P +W_{non-conservative}[/latex].

Rearranging this equation, we finally get that [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex].

As we can see from the equation above, when the non-conservative forces oppose the motion of the object, the work done by these forces is negative, causing a decrease in the mechanical energy of the system. When the non-conservative forces do positive work, energy is added to the system. If the sum of the non-conservative forces is zero then [latex]\scriptsize \Delta E_K = -\Delta E_P[/latex] and mechanical energy is conserved.

Take note!

For situations where there is a change in the kinetic and/or the potential energy of an object, the total work done by the non-conservative forces to enact this change can be calculated using:
[latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex].

Once the total work of these forces is known, the total nett non-conservative forces or the distance over which the work is done can be calculated.

Example 2.3

Question adapted from Everything Science Grade 12 Worked example 9 page 242

Consider the situation where a football player slides to a stop on level ground. Using energy considerations, calculate the distance a [latex]\scriptsize 65.0~\text{kg}[/latex] football player slides, given that his initial speed is [latex]\scriptsize 6.00~\text{m.s}^{-1}[/latex] and the force of friction against him is a constant [latex]\scriptsize 450~\text{N}[/latex].

Solution

We know that the frictional force will act in the opposite direction to the player’s initial motion to reduce his kinetic energy to zero. Most of this kinetic energy will be converted to heat, deformation of the grass and some sound. While the total energy of the system is conserved, the mechanical energy of the player is not. We know this because there is a frictional non-conservative force acting on the player.

Because the frictional force acts to reduce the player’s mechanical energy, we know that it does negative work on the player; [latex]\scriptsize \theta = 180^\circ[/latex]. Therefore, [latex]\scriptsize \cos \theta = -1[/latex].

Because the player is on level ground, there is no change in the potential energy. Hence [latex]\scriptsize \Delta E_P = 0[/latex].

We know that [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex]. But [latex]\scriptsize \Delta E_P = 0[/latex]. Therefore, [latex]\scriptsize W_{non-conservative} = \Delta E_K[/latex]. This is basically the original work-energy theorem.

[latex]\scriptsize \begin{align*} m &= 65~\text{kg}\\ v_i &= 6~\text{m.s}^{-1}\\ F_{friction} &= 450~\text{N}\\ W_{non-conservative} &= \Delta E_K\\ \therefore F_{friction} \Delta x \cos \theta &= E_{Kf} – E_{Ki}\\ \therefore -F_{friction} \Delta x &= 0 – E_{Ki} &&(\theta = 180^\circ~\text{and } v_f = 0~\text{m.s}^{-1}~\text{so }E_{Kf} = 0~\text{J})\\ \therefore \Delta x &= \displaystyle \frac{-E_{Ki}}{F_{friction}}\\ \therefore \Delta x &= - \displaystyle \frac{\displaystyle \frac{1}{2} mv^2}{F_{friction}}\\ &= -\displaystyle \frac{1}{2} \times 65~\text{kg} \times \displaystyle \frac{(6~\text{m.s}^{-1})^2}{450~\text{N}}\\ &= 2.60~\text{m} \end{align*}[/latex]

The player will stop after [latex]\scriptsize 2.60~\text{m}[/latex].

Exercise 2.1

1. Consider the falling and rolling motion of a [latex]\scriptsize 2~\text{kg}[/latex] ball in the following two resistance-free situations. In one situation, the ball falls off the top of the platform to the floor. In the other situation, the ball rolls from the top of the platform along the staircase-like pathway to the floor.
   
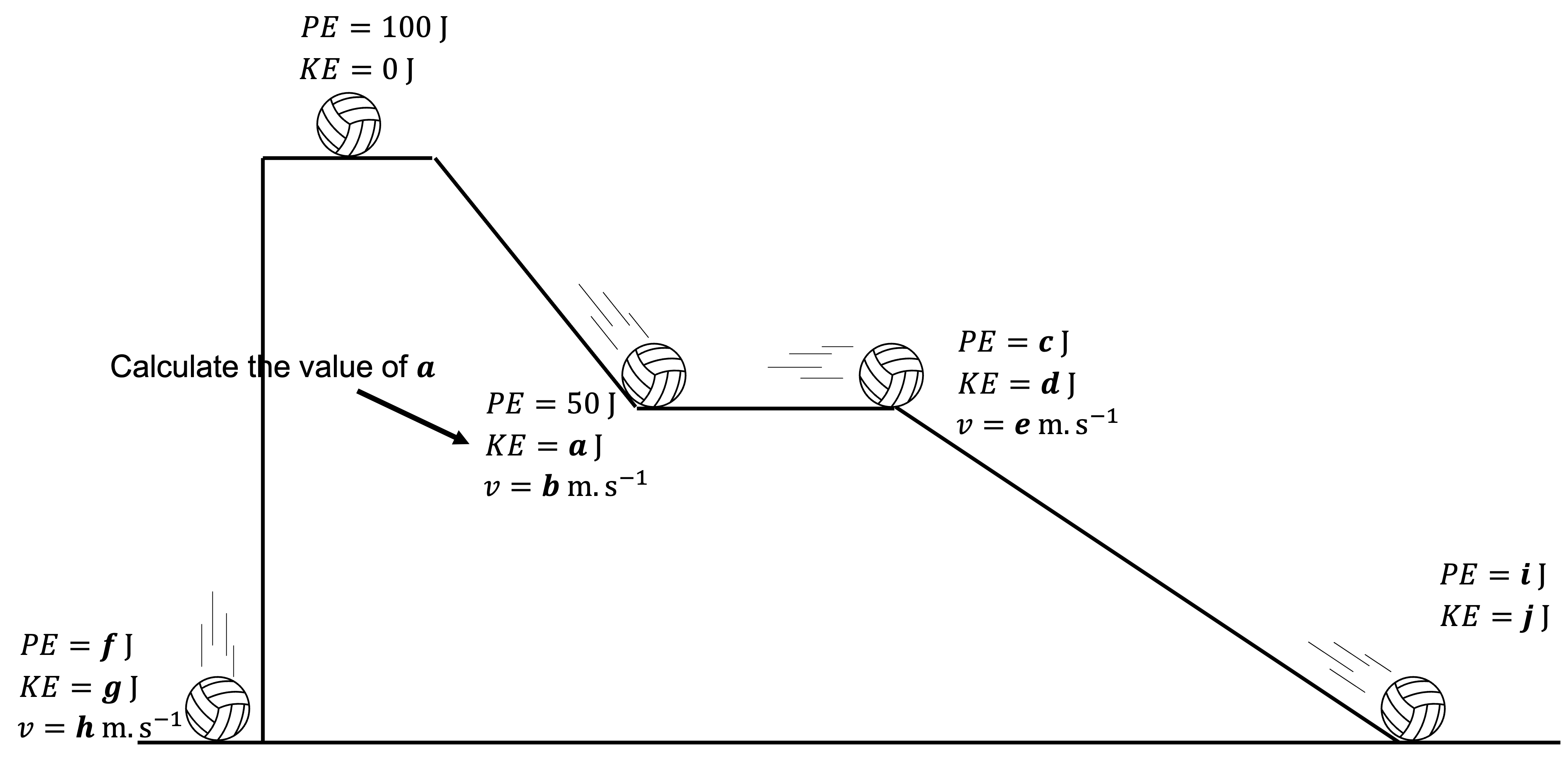
   For each situation:
   1. indicate what types of forces are doing work upon the balls
   2. indicate whether the energy of each ball is conserved and explain why
   3. calculate values for all unknowns a – k in the diagram.
2. At the end of a roller coaster ride, the [latex]\scriptsize 6~000~\text{kg}[/latex] train of cars (including passengers) is slowed from a speed of [latex]\scriptsize 20~\text{m.s}^{-1}[/latex] to a speed of [latex]\scriptsize 5~\text{m.s}^{-1}[/latex] over a distance of [latex]\scriptsize 20~\text{m}[/latex] up an incline that has a total vertical height of [latex]\scriptsize 2~\text{m}[/latex]. Calculate the braking force required to slow the train of cars by this amount.
3. A girl on roller blades has an initial velocity of [latex]\scriptsize 10~\text{m.s}^{-1}[/latex]. She has a mass of [latex]\scriptsize 50~\text{kg}[/latex] and coasts straight up a hill that is [latex]\scriptsize 2.5~\text{m}[/latex] height.
   
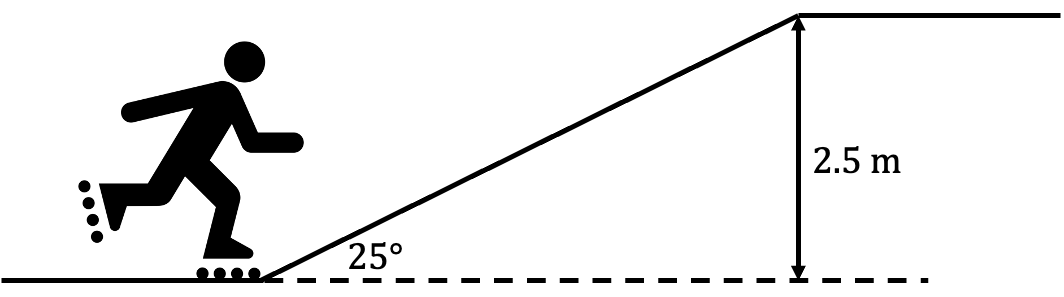
   1. What distance does she travel up the hill?
   2. What is her speed at the top of the hill if the total frictional force acting on her is [latex]\scriptsize 1.5~\text{N}[/latex]?

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• Conservative forces (or internal forces) conserve mechanical energy.
• Non-conservative forces (or external forces) do not conserve mechanical energy.
• The work done by conservative forces does not depend on the path taken.
• The work done by non-conservative forces depends on the path taken.
• The work-energy theorem states that total nett work is equal to the change in kinetic energy; therefore [latex]\scriptsize W_{nett} = \Delta E_K = E_{Kf} – E_{Ki}[/latex].
• The work-energy theorem can be rearranged to calculate the total non-conservative work done on an object as [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex].

Unit 2: Assessment

Suggested time to complete: 35 minutes

1. A shopping trolley full of groceries is sitting at the top of a [latex]\scriptsize 2.0~\text{m}[/latex] hill. The trolley rolls down the hill and hits a stump at the bottom of the hill. Upon impact, a [latex]\scriptsize 250~\text{g}[/latex] can of baked beans flies horizontally out of the shopping cart and hits a parked car with an average force of [latex]\scriptsize 500~\text{N}[/latex]. How deep a dent is made in the car (i.e. over what distance does the [latex]\scriptsize 500~\text{N}[/latex] force act upon the can of beans before bringing it to a stop)?
2. A rope is attached to a [latex]\scriptsize 40.0~\text{kg}[/latex] crate to pull it up a frictionless incline at constant speed to a height of [latex]\scriptsize 3~\text{m}[/latex]. A diagram of the situation and a free-body diagram are shown below.
   
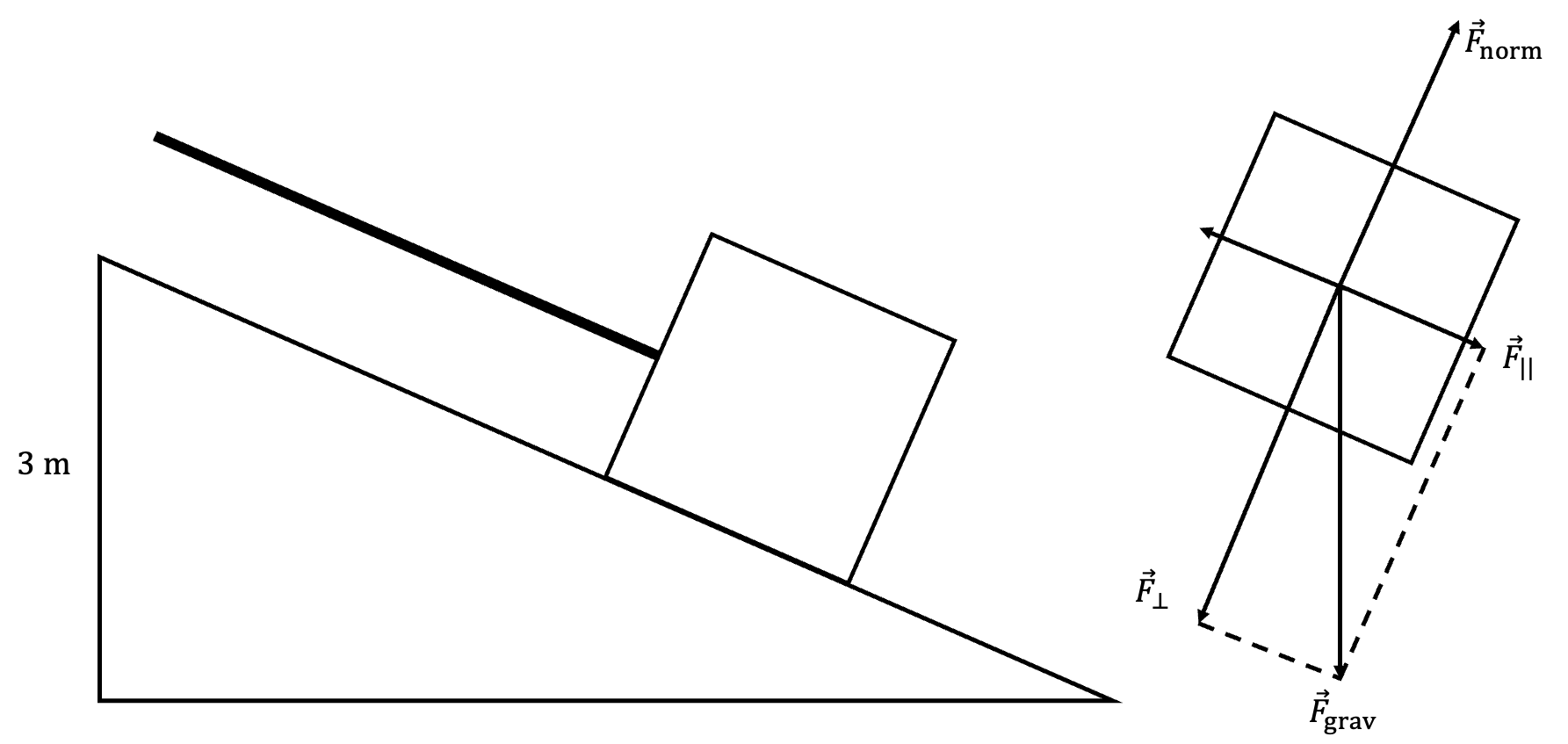
   Note that the force of gravity has two components (parallel and perpendicular components); the parallel component balances the applied force, and the perpendicular component balances the normal force.
   1. Of the forces acting on the crate, which ones do work?
   2. Based upon the types of forces acting upon the system and their classification as conservative and non-conservative forces, is mechanical energy conserved? Explain.
   3. Calculate the amount of work done upon the crate.

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. The only force doing work on the ball is gravity.
   2. Since gravity is a conservative force, the total mechanical energy of the ball is conserved. Therefore, the total mechanical energy of the ball remains 100 J.
   3. a – [latex]\scriptsize 50~\text{J}[/latex]. If the ball has half its original potential energy, the other half must be been converted into kinetic energy.
      b – [latex]\scriptsize 7.07~\text{m.s}^{-1}[/latex] [latex]\scriptsize E_K=\displaystyle \frac{1}{2}mv^2 \therefore v=\sqrt{\displaystyle \frac{100}{2}}=\sqrt{50}[/latex].
      c – [latex]\scriptsize 50~\text{J}[/latex]. The ball is at the same height, therefore, its potential energy is still [latex]\scriptsize 50~\text{J}[/latex].
      d – [latex]\scriptsize 50~\text{J}[/latex]. There is no resistance, therefore, its kinetic energy is still [latex]\scriptsize 50~\text{J}[/latex].
      e – [latex]\scriptsize 7.07~\text{m.s}^{-1}[/latex]. There is no resistance, therefore, its velocity is still [latex]\scriptsize 7.07~\text{m.s}^{-1}[/latex] [latex]\scriptsize 50~\text{J}[/latex].
      f – [latex]\scriptsize 0~\text{J}[/latex]. The ball is on the ground, therefore, it has no potential energy.
      g – [latex]\scriptsize 100~\text{J}[/latex]. The ball is on the ground, therefore, all its potential energy has been converted to kinetic energy.
      h – [latex]\scriptsize 10~\text{m.s}^{-1}[/latex] [latex]\scriptsize E_K=\displaystyle \frac{1}{2}mv^2 \therefore v=\sqrt{\displaystyle \frac{200}{2}}=\sqrt{100}[/latex].
      i – [latex]\scriptsize 0~\text{J}[/latex]. The ball is on the ground, therefore, it has no potential energy.
      j – [latex]\scriptsize 100~\text{J}[/latex]. The ball is on the ground, therefore, all its potential energy has been converted to kinetic energy.
      k – [latex]\scriptsize 10~\text{m.s}^{-1}[/latex] [latex]\scriptsize E_K=\displaystyle \frac{1}{2}mv^2 \therefore v=\sqrt{\displaystyle \frac{200}{2}}=\sqrt{100}[/latex].
2. .
   [latex]\scriptsize \begin{align*} m &= 6~000~\text{kg}\\ vi &= 20~\text{m.s}^{-1}\\ vf &= 5~\text{m.s}^{-1}\\ \Delta x &= 20~\text{m}\\ h &= 2~\text{m} \end{align*}[/latex]
   .
   [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex]
   Where:
   • [latex]\scriptsize W_{non-conservative} = F_{brake} \Delta x \cos \theta = -F_{brake} \Delta x[/latex]
   • [latex]\scriptsize \Delta E_K = E_{Kf} – E_{Ki} = \displaystyle \frac{1}{2} mv_f^2 – \displaystyle \frac{1}{2} mv_i^2 = \displaystyle \frac{1}{2} m (v_f^2 – v_i^2)[/latex]
   • [latex]\scriptsize \Delta E_P = mgh[/latex]
     .
     [latex]\scriptsize \begin{align*} \therefore {-F_{brake}}{\Delta x} &= \displaystyle \frac{1}{2} m (v_f^2 - v_i^2) + mgh\\ \therefore F_{brake} &= -\displaystyle \frac{\left(\displaystyle \frac{1}{2} m (v_f^2 - v_i^2) + mgh\right)}{\Delta x}\\ &=-\displaystyle \frac{(\displaystyle \frac{1}{2} \times 6~000~\text{kg} \left((5~\text{m.s}^{-1})^2 - (20~\text{m.s}^{-1})^2\right) + 6~000~\text{kg} \times 9.8~\text{m.s}^{-2} \times 2~\text{m})}{20~\text{m}}\\ &= 50~370~\text{N} \end{align*}[/latex]
     .
     Therefore, the braking force required is [latex]\scriptsize 50~370~\text{N}[/latex].
3. .
   1. We can use trigonometry to calculate the distance up the hill.
      [latex]\scriptsize \begin{align*} \sin 25^\circ &= \displaystyle \frac{2.5~\text{m}}{d}\\ \therefore d &= \displaystyle \frac{2.5~\text{m}}{\sin25^\circ}\\ &= 5.92~\text{m} \end{align*}[/latex]
   2. The value calculated in a. is [latex]\scriptsize \Delta x[/latex] in calculation of work.
      [latex]\scriptsize \begin{align*} m &= 60~\text{kg}\\ \Delta x &= 5.92~\text{m}\\ F_{friction} &= 1.5~\text{N}\\ h &= 2.5~\text{m}\\ v_i &= 10~\text{m.s}^{-1} \end{align*}[/latex]
      .
      We need to calculate the final velocity of the girl at the top of the hill. In this case, she will lose kinetic energy and gain potential energy.
      .
      [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex]
      Where:
      • [latex]\scriptsize W_{non-conservative} = F_{friction} \Delta x \cos \theta = -F_{friction} \Delta x[/latex]
      • [latex]\scriptsize \Delta E_K = E_{Kf} – E_{Ki} = \displaystyle \frac{1}{2} mv_f^2 – \displaystyle \frac{1}{2} mv_i^2 = \displaystyle \frac{1}{2} m (v_f^2 – v_i^2)[/latex]
      • [latex]\scriptsize \Delta E_P = mgh[/latex]
        .
        [latex]\scriptsize \begin{align*} \therefore -F_{friction} \Delta x &= \displaystyle \frac{1}{2} m(v_f^2 - v_i^2) + mgh\\ \therefore -F_{friction} \Delta x - mgh &= \displaystyle \frac{1}{2} m(v_f^2 - v_i^2)\\ \therefore -2\displaystyle \frac{(F_{friction} \Delta x+ mgh)}{m} &= v_f^2 - v_i^2\\ \therefore v_f^2 &= -2\displaystyle \frac{(F_{friction} \Delta x + mgh)}{m} + v_i^2\\ &=-2 \displaystyle \frac{(- 1.5~\text{N} \times 5.92~\text{m})+(50~\text{kg} \times 9.8~\text{m.s}^{-2} \times 2.5~\text{m})}{50~\text{kg}} + (10~\text{m.s}^{-1})^2\\ &= 51.3552~\text{m.s}^{-2}\\ \therefore v_f &= 7.17~\text{m.s}^{-1} \end{align*}[/latex]
        .
        Her speed at the top of the hill will be [latex]\scriptsize 7.17~\text{m.s}^{-1}[/latex].

Back to Exercise 2.1

Unit 2: Assessment

1. The only force acting on the trolley and, therefore the tin, is gravity. Therefore, mechanical energy is conserved and all the potential energy at the top of the hill is converted to kinetic energy at the bottom of the hill.
   .
   [latex]\scriptsize \begin{align*} m &= 250~\text{g} = 0.25~\text{kg}\\ h &= 2~\text{m}\\ E_P~\text{at the top of the hill }&= mgh\\ &= 0.25~\text{kg} \times 9.8~\text{m.s}^{-2} \times 2~\text{m}\\ &= 4.9~\text{J}\\ \therefore E_K~\text{at the bottom of the hill }&= 4.9~\text{J} \end{align*}[/latex]
   .
   When the tin hits the car, it loses kinetic energy due to the force applied to it by the body of the car. This is a non-conservative force. Therefore, mechanical energy is not conserved. All the can’s kinetic energy is transformed into the energy needed to dent the car. The force the car body applies to the can is [latex]\scriptsize 500~\text{N}[/latex] in the opposite direction to the motion of the can.
   .
   [latex]\scriptsize \begin{align*} V_f &= 0~\text{m.s}^{-1}\\ F &= 500~\text{N}\\ W_{nett} &= \Delta E_K\\ \therefore F \Delta x \cos \theta &= E_{Kf} – E_{Ki}\\ \therefore 500~\text{N} \Delta x (-1) &= 0~\text{J} – 4.9~\text{J}\\ \therefore \Delta x &= \displaystyle \frac{4.9~\text{J}}{500~\text{N}}\\ &= 0.0098~\text{m} \end{align*}[/latex]
   .
   Therefore, It will take [latex]\scriptsize 9.8~\text{mm}[/latex] for the car to stop the can. In other words, the dent will be [latex]\scriptsize 9.8~\text{mm}[/latex] deep.
2. .
   1. Both gravity (because of the component of gravity acting parallel to the direction of motion) and the applied tension force in the rope do work. The normal force is perpendicular to the direction of motion so does no work.
   2. The applied force is non-conservative. Since it does work on the box, the mechanical energy of the box is not conserved.
   3. [latex]\scriptsize W_{non-conservative} = \Delta E_K + \Delta E_P[/latex]
      Where
      • [latex]\scriptsize \Delta E_K = 0~\text{J}[/latex] (there is no change in velocity)
      • [latex]\scriptsize \Delta E_P = mgh[/latex]
        .
        [latex]\scriptsize \begin{align*} \therefore W_{non-conservative} &= mgh\\ &= 40~\text{kg} \times 9.8~\text{m.s}^{-2} \times 3~\text{m}\\ &= 1~176~\text{J} \end{align*}[/latex]
        .
        The work done by the non-conservative force in pulling the box up the incline is [latex]\scriptsize 1~176~\text{J}[/latex].
        .
        Note that it does not matter what the angle of the incline or distance of the incline is. Because there is no change in kinetic energy, all the non-conservative work is done ‘against gravity’. And the work done by gravity, being a conservative force, does not depend on the path taken; only the start and end points i.e. the change in height.

Back to Unit 2: Assessment