Matter and Materials: State, evaluate and apply properties of fluids on everyday life and industrial contexts
Unit 1: Properties of Fluids
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Define, describe and calculate hydrostatic pressure in relation to the density and depth of a liquid.
- Use Pascal’s principle and state common uses of this principle.
- Show the relationship between pressure and the speed of fluid flow using a Venturi meter.
What you should know
Before you start this unit, make sure you can
- Describe a fluid. Refer to level 3 subject outcome 5.4 units 1 and 2 if you need help with this.
- State and explain what density and pressure are. Refer to level 3 subject outcome 5.4 units 1 and 2 if you need help with this.
- Explain and calculate mechanical advantage. Refer to level 3 subject outcome 2.5 if you need help with this.
- State and explain the mechanical properties of matter. See level 3 subject outcome 5.1 if you need help with this.
Introduction
We know that there are four basic states of matter – solid, liquid, gas and plasma (see figure 1). Together, liquids and gases are called fluids. Fluids take the shape of the container they are in. They can also be made to move from an area of high pressure to an area of low pressure. In other words, fluids can flow.

But we know that liquids and gases have some important differences. For example, while gases take up the whole volume of the container they are in, liquids do not. Gases also tend to be far more compressible. By applying a force, we can greatly decrease the volume that a gas occupies. The volume of a gas also changes far more with respect to temperature than does a liquid’s volume. As the temperature of a gas increases, so does its volume.
We focused on many of these properties of gases in level 3 subject outcome 5.4. In this unit, we will focus on liquids and we will make two important assumptions about liquids:
- liquids are incompressible – their volume cannot be reduced by apply a force
- the volume of liquids does not change with temperature.
Now, of course, in the real world, all liquids can be compressed to some degree. It is just that the forces required are usually very, very large. Also, the volume of liquids does increase with a rise in temperature. It is just that any change in the volume is usually very, very small.
Hydrostatic pressure
To understand hydrostatic pressure, we need to make sure that we understand what pressure and density are. Let’s start with density.
Density
You may have heard this old trick question: “Which weighs more: a ton of bricks or a ton of feathers?” The answer, of course, is that they both weight exactly the same – a ton ([latex]\scriptsize 1~000~\text{kg}[/latex]) (see figure 2).
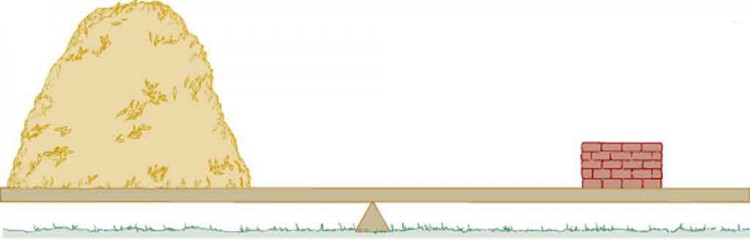
The volume of a ton of feathers, however, will be much greater than the volume of a ton of bricks. The ‘stuff’ of feathers is much less tightly packed than the ‘stuff’ of bricks. They have different densities.
Density is the mass of a unit volume of a substance. It is a measure of how tightly packed the matter of a substance is. The more tightly packed the matter, the more mass a given volume of the substance will have.
Density ([latex]\scriptsize \rho[/latex] the Greek letter rho) is therefore defined as mass divided by volume or [latex]\scriptsize \rho = \displaystyle \frac{m}{V}[/latex]. Density has the SI units of [latex]\scriptsize \text{kg.m}^{-3}[/latex].
Take note!
Density is mass per unit of volume.
[latex]\scriptsize \rho=\displaystyle \frac{m}{V}[/latex]
Every solid, liquid and gas has a specific, defined density at standard temperature and pressure. Table 1 shows the densities of some common substances. Notice that the densities of solids are generally greater than liquids and that the density of liquids is generally greater than gases.
| Solids (at [latex]\scriptsize 0.0~\text{C}^{\circ}[/latex]) |
Liquids (at [latex]\scriptsize 0.0~\text{C}^{\circ}[/latex]) |
Gases (at [latex]\scriptsize 0.0~\text{C}^{\circ}[/latex] and [latex]\scriptsize 101.3~\text{kPa}[/latex]) |
|||
| Substance | [latex]\scriptsize \rho~(\text{kg.m}^{-3})[/latex] | Substance | [latex]\scriptsize \rho~(\text{kg.m}^{-3})[/latex] | Substance | [latex]\scriptsize \rho~(\text{kg.m}^{-3})[/latex] |
| Aluminium | [latex]\scriptsize 2.70 \times 10^3[/latex] | Benzene | [latex]\scriptsize 8.79 \times 10^2[/latex] | Air | [latex]\scriptsize 1.29 \times 10^0[/latex] |
| Bone | [latex]\scriptsize 1.90 \times 10^3[/latex] | Blood | [latex]\scriptsize 1.05 \times 10^3[/latex] | Carbon dioxide | [latex]\scriptsize 1.98 \times 10^0[/latex] |
| Brass | [latex]\scriptsize 8.44 \times 10^3[/latex] | Ethyl alcohol | [latex]\scriptsize 8.06 \times 10^2[/latex] | Carbon monoxide | [latex]\scriptsize 1.25 \times 10^0[/latex] |
| Concrete | [latex]\scriptsize 2.40 \times 10^3[/latex] | Gasoline | [latex]\scriptsize 6.80 \times 10^2[/latex] | Helium | [latex]\scriptsize 1.80 \times 10^{-1}[/latex] |
| Copper | [latex]\scriptsize 8.92 \times 10^3[/latex] | Mercury | [latex]\scriptsize 1.36 \times 10^4[/latex] | Hydrogen | [latex]\scriptsize 9.00 \times 10^{-2}[/latex] |
| Glass | [latex]\scriptsize 2.60 \times 10^3[/latex] | Olive oil | [latex]\scriptsize 9.20 \times 10^2[/latex] | Methane | [latex]\scriptsize 7.2 \times 10^{-2}[/latex] |
| Gold | [latex]\scriptsize 1.93 \times 10^4[/latex] | Water | [latex]\scriptsize 1 \times 10^3[/latex] | Nitrogen | [latex]\scriptsize 1.25 \times 10^0[/latex] |
| Granite | [latex]\scriptsize 2.70 \times 10^3[/latex] | Oxygen | [latex]\scriptsize 1.43 \times 10^0[/latex] | ||
| Iron | [latex]\scriptsize 7.86 \times 10^3[/latex] | ||||
| Lead | [latex]\scriptsize 1.13 \times 10^4[/latex] | ||||
| Oak | [latex]\scriptsize 7.10 \times 10^2[/latex] | ||||
| Pine | [latex]\scriptsize 2.70 \times 10^3[/latex] | ||||
| Platinum | [latex]\scriptsize 2.14 \times 10^4[/latex] | ||||
| Polystyrene | [latex]\scriptsize 1.00 \times 10^2[/latex] | ||||
| Uranium | [latex]\scriptsize 1.87 \times 10^3[/latex] | ||||
Example 1.1
A dam has a surface area of [latex]\scriptsize 40.0~\text{km}^2[/latex] and an average depth of [latex]\scriptsize 45.0~\text{m}[/latex]. What mass of water is held in the reservoir? Assume the density of water is [latex]\scriptsize 1~000~\text{kg.m}^{-3}[/latex].
Solution
The first thing we need to do is convert the surface are of the dam from [latex]\scriptsize \text{km}^2[/latex] to [latex]\scriptsize \text{m}^2[/latex].
[latex]\scriptsize 40.0~\text{km}^2=40\times (1~000\times 1~000)=40~000~000~\text{m}^2[/latex]
The total volume of water is:
[latex]\scriptsize \begin{align*} V&=\text{surface area}\times \text{depth}\\ &=40~000~000~\text{m}^2\times 45.0~\text{m}\\ &=1~800~000~000~\text{m}^3\\ &=1.8\times 10^9~\text{m}^3 \end{align*}[/latex]
[latex]\scriptsize \begin{align*} \rho&=\displaystyle \frac{m}{V}\\ \therefore m&=\rho \times V\\ &=1~000~\text{kg.m}^{-3} \times 1.8\times 10^9~\text{m}^3\\ &=1.8 \times 10^12\text{kg} \end{align*}[/latex]
Pressure
All fluids exert a pressure. Pressure is defined as the force divided by the area perpendicular to the force over which the force is applied. In other words, [latex]\scriptsize P=\displaystyle \frac{F}{A}[/latex]. Pressure has the SI units of [latex]\scriptsize \text{N.m}^{-2}[/latex].
Force is most often measured in pascals (Pa), in recognition of the work Blaise Pascal did in defining and explaining pressure. We define [latex]\scriptsize 1~\text{Pa}[/latex] as being equal to [latex]\scriptsize 1~\text{N.m}^{-2}[/latex].
Take note!
Pressure is force divided by the perpendicular unit area.
[latex]\scriptsize P=\displaystyle \frac{F}{A}[/latex]
[latex]\scriptsize 1~\text{Pa} = 1~\text{N.m}^{-2}[/latex]
Example 1.2
An astronaut is doing a spacewalk to fix a broken satellite. The pressure gauge on his air tank reads [latex]\scriptsize 5.58 \times 10^6~\text{Pa}[/latex]. His air tank is a cylinder with a diameter of [latex]\scriptsize 35~\text{cm}[/latex]. With what force does the air inside the tank press on the flat circular bottom of his tank?
Solution
Calculate the area of the flat circular bottom of the tank. To do this, we need to find the radius (in metres).
[latex]\scriptsize r=\displaystyle \frac{35~\text{cm}}{2}=17.5~\text{cm}=0.175~\text{m}[/latex]
[latex]\scriptsize \begin{align*} A&=\pi r^2\\ &=\pi \times \left(0.175~\text{m}\right)^2\\ &=0.0962~\text{m}^2 \end{align*}[/latex]
[latex]\scriptsize \begin{align*} P&=\displaystyle \frac{F}{A}\\ \therefore F&=P \times A\\ &=5.58 \times 10^6~\text{Pa} \times 0.0962~\text{m}^2\\ &=536~796~\text{N}\\ &=536.796\times 10^3~\text{N} \end{align*}[/latex]
It is important to note that the forces exerted by fluids because of pressure are only exerted perpendicular to surfaces. Fluids cannot exert sideways or shear forces.
Fluid pressure also has no direction. The force can be exerted in any direction. When someone is swimming through water, the pressure is exerted on all sides of the swimmer, since the water would flow into the space they occupy if they were not there. The arrows in figure 3 below represent the directions and sizes of the forces exerted at various points on the swimmer (all perpendicular). Note that the forces are larger underneath the swimmer, due to greater depth, giving a net upward or that is balanced by the weight of the swimmer.
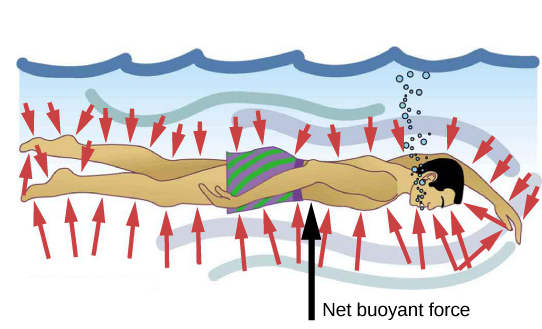
Pressure at a depth
We noted above that the forces acting on the underside of the swimmer in figure 3 were greater because the depth was greater. Let’s explore the relationship between depth and pressure in more detail.
If you have ever dived into a deep pool or body of water, you might have noticed that, at a certain depth, your ears start to hurt. This is because the deeper you go under water, the greater the pressure exerted by the water. A simple way to think of this is that the deeper you go, the more water there is vertically above you. The more water, the greater the weight of this water, the more force it will be able to exert per unit area.
Example 1.3
The reservoir in example 1.1 had an average depth of [latex]\scriptsize 45.0~\text{m}[/latex]. What is the pressure exerted by the water alone on the bottom of the reservoir at a depth of [latex]\scriptsize 45.0~\text{m}[/latex]?
Solution
For convenience, we will consider a column of water that has a cross-sectional area of [latex]\scriptsize 1~\text{m}^2[/latex].
The volume of such a column of water (cross-sectional area of [latex]\scriptsize 1~\text{m}^2[/latex] and height [latex]\scriptsize 45~\text{m})[/latex] will be [latex]\scriptsize 45~\text{m}^3[/latex]. Therefore, the mass of this column of water will be:
[latex]\scriptsize \begin{align*} m&=\rho \times V\\ &=1~000~\text{kg.m}^{-3} \times 45~\text{m}^3\\ &=45~000\text{kg}\\ &=45\times 10^3~\text{kg} \end{align*}[/latex]
Therefore, the force with which this column of water pushes down on the bottom of the reservoir will be its weight i.e. [latex]\scriptsize mg = 45~000\text{kg} \times 9.8~\text{m.s}^{-2}=441~000~\text{N}[/latex].
[latex]\scriptsize \begin{align*} P&=\displaystyle \frac{F}{A}\\ &=\displaystyle \frac{441~000~\text{N}}{1~\text{m}^2} &=441~000~\text{Pa}\\ &=4.41 \times 10^5~\text{Pa} \end{align*}[/latex]
We can derive a simple expression for the pressure due to the weight of any fluid. We know from the above example that:
[latex]\scriptsize P=\displaystyle \frac{mg}{A}[/latex]
We can find the mass of the fluid from its volume and density:
[latex]\scriptsize m=\rho V[/latex]
The volume of the fluid related to the dimensions of a right prism container where [latex]\scriptsize A[/latex] is the area of the base and [latex]\scriptsize h[/latex] is the vertical height is as follows:
[latex]\scriptsize V=Ah[/latex]
Therefore, we can say that:
[latex]\scriptsize m=\rho Ah[/latex]
If we use this in the expression for pressure, we get:
[latex]\scriptsize P=\displaystyle \frac{(\rho Ah)g}{A}[/latex]
If we cancel the area terms and rearrange some other terms we get:
[latex]\scriptsize P=h\rho g[/latex]
Take note!
The pressure due to the weight of a fluid is given by:
[latex]\scriptsize P=h\rho g[/latex]
where [latex]\scriptsize h[/latex] is the vertical height of the fluid above the point where the pressure is being measured, [latex]\scriptsize \rho[/latex] is the density of the fluid and [latex]\scriptsize g[/latex] is the acceleration due to gravity (see figure 4).
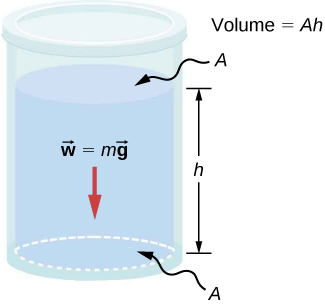
While you may not realise it, the air around you exerts an enormous pressure on your body. Use the expression above to calculate what this pressure is at sea level if the height of the column of air above you is [latex]\scriptsize 8.440~\text{km}[/latex] and the density of air is [latex]\scriptsize 1.225~\text{kg.m}^{-3}[/latex].
Did you get that the air exerts a pressure on your body of about [latex]\scriptsize 101~325~\text{Pa}[/latex] at sea level. Obviously, the higher up you go, the less this atmospheric pressure is because there is less air above you. You will sometimes see atmospheric pressure measured in atmospheres.
[latex]\scriptsize 1~\text{atmosphere}=101~325~\text{Pa}[/latex].
You don’t feel this atmospheric pressure because the pressure inside your body is roughly the same as the atmospheric pressure outside. Therefore, both forces acting on our bodies cancel out and we do not feel uncomfortable.
Now when you are in water, your body does not only experience the pressure due to the water. It also experiences the pressure of the atmosphere pushing down on the surface of the water as well. Do the following activity to learn more.
Activity 1.1: Investigate hydrostatic pressure
Time required: 10 minutes
What you need:
- an internet connection
What to do:
- Open the interactive simulation called Under Pressure
.
.
You will find four icons listed in the bottom left-hand corner. Make sure the top icon is selected. Make sure also that the Fluid Density is set to [latex]\scriptsize 1~000~\text{kg.m}^{-3}[/latex] (in other words so that we are dealing with water) and the Gravity is set to ‘Earth’. - Click and drag the pressure gauge to measure the air pressure directly above the grass and above the surface of the water. What is the pressure in each case? Why are they different readings?
- Now click on the Grid checkbox to turn the grid on. You should see that the level of the water is about [latex]\scriptsize 1.5~\text{m}[/latex]. Calculate the pressure at the bottom of the tank if this pressure is the combination of the atmospheric pressure at the surface of the water and the pressure due to the weight of the water itself. Use your pressure gauge to confirm.
- Click on the top stopper to fill the tank with water. Recalculate the pressure at the bottom of the tank due to the atmospheric pressure and the pressure due to the weight of the water. Use your pressure gauge to confirm.
- Now click on the third icon on the left-hand side. Make sure once again that the density and gravity are [latex]\scriptsize 1~000~\text{kg.m}^{-3}[/latex] and ‘Earth’ respectively.
- First, measure the pressure at the bottom of both parts of the tank. Is the pressure the same. Why?
- Place the pressure gauge at the bottom of the left-hand part of the tank. You will see some masses on the left-hand side. Drag the [latex]\scriptsize 500~\text{kg}[/latex] mass and drop it into the dotted box as indicated. What happens to the pressure at the bottom of the left-hand part of the tank? Why is this? What happens to the water level in the right-hand part of the tank? Why is this? Are the pressures at the bottom of both halves of the tank still the same? Why?
- What happens when you add either or both of the other masses?
What did you find?
- This is what your screen should look like.
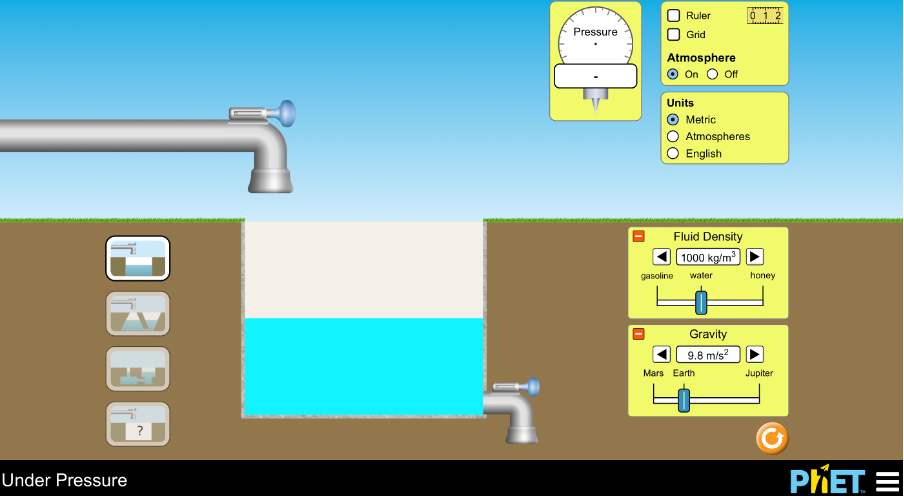
- The pressure just above the grass is [latex]\scriptsize 101.325~\text{kPa}[/latex]. The pressure just above the surface of the water is [latex]\scriptsize 101.524~\text{kPa}[/latex]. The pressure at the surface of the water is greater than just above the ground because the surface of the water is below the ground and so the column of air exerting this force is higher.
- Pressure at surface of the water is [latex]\scriptsize 101.524~\text{kPa}[/latex]. The pressure at the bottom of the tank due to the weight of the water is calculated as follows:
[latex]\scriptsize \begin{align*} P&=h\rho g\\ &=1.5~\text{m}\times 1~000~\text{kg.m}^{-3}\times 9.8~\text{m.s}^{-2} &=14~700~\text{Pa}\\ &=14.7~\text{kPa} \end{align*}[/latex]
Therefore, the total pressure at the bottom of the tank is [latex]\scriptsize 101.524~\text{kPa} + 14.7~\text{kPa}=116.224~\text{kPa}[/latex].
.
The pressure gauge reads [latex]\scriptsize 115.968~\text{kPa}[/latex]. While it is not exact, it is very close. - If we fill the tank, the depth of the water will be [latex]\scriptsize 3~\text{m}[/latex]. The pressure at the surface of the water will be [latex]\scriptsize 101.325~\text{kPa}[/latex]. The pressure at the bottom of the tank due to the weight of the water will be:
[latex]\scriptsize \begin{align*} P&=h\rho g\\ &=3~\text{m}\times 1~000~\text{kg.m}^{-3}\times 9.8~\text{m.s}^{-2} &=29~400~\text{Pa}\\ &=29.4~\text{kPa} \end{align*}[/latex]
Therefore, the total pressure at the bottom of the tank is [latex]\scriptsize 101.355~\text{kPa} + 29.4~\text{kPa}=130.725~\text{kPa}[/latex].
.
The pressure gauge reads [latex]\scriptsize 130.650~\text{kPa}[/latex]. While it is not exact, it is very close. - This is what your screen should look like.
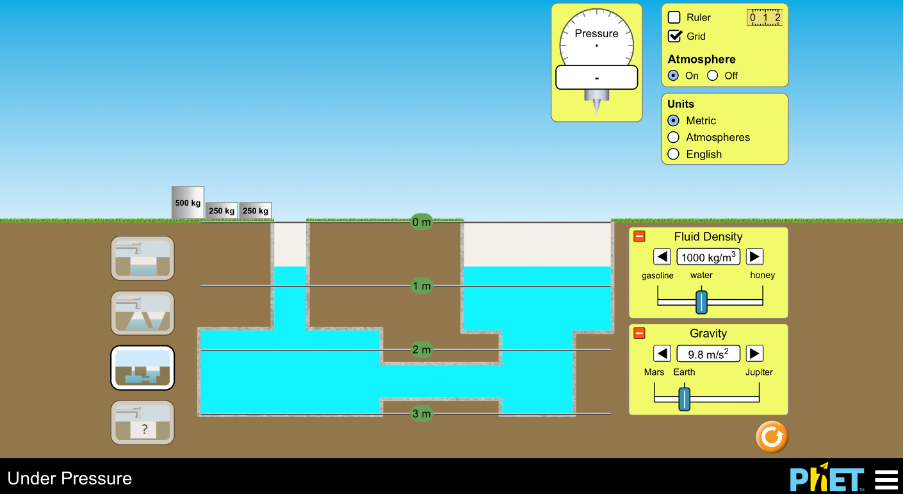
- The pressure at the bottom of both parts of the tank is [latex]\scriptsize 123.798~\text{kPa}[/latex]. It is the same because the height of the water vertically above each bottom is exactly the same. Therefore, the atmospheric pressure at the surface and the pressure at the bottom due to the weight of the water is the same.
- The mass pushes down the surface of the water. Therefore, the pressure at the surface is now greater. It is atmospheric pressure plus the weight of the [latex]\scriptsize 500~\text{kg}[/latex] mass. Even though the height of the water above the bottom of the tank is lower, the pressure still increases because the weight of the mass is greater than the volume of water being displaced. The solid mass has a density greater than water. The water level in the right-hand part of the tank rises. The water being displaced on the left has to go somewhere. The water is non-compressible. The pressure at the bottom of the right-hand part of the tank has also increased and is still the same as that at the bottom of the left-hand tank. This pressure increases because the height of the water has increased and the weight of the water has increased by a greater amount than the decrease in the atmospheric pressure at the surface.
- As you place additional masses, the pressure in the tank increases and the water level on the right-hand side increases.
In activity 1.1, we saw that the pressure at the bottom of a container of fluid exposed to the atmosphere is the sum of the pressure due to the weight of the fluid and the atmospheric pressure at the surface of the fluid.
It is important to note that the shape of the container has no effect on the pressure. All that matters is the density of the fluid and its vertical height. Have a look at each of the pressure gauges in figure 5. In all three cases the shape of the container is different but the level of the liquid is the same and the pressure gauges all show the same reading. This is because pressure is the force per unit area acting perpendicular to a surface. Therefore, we are only concerned with the height of a vertical column of fluid above the surface.

We also learnt that when a force is exerted on a fluid, this changes the pressure the fluid exerts and that this change in pressure is transmitted throughout the fluid. This is an important principle we will turn our attention to next.
Exercise 1.1
- Which of the following equations is not correct:
- [latex]\scriptsize F=m \times a[/latex]
- [latex]\scriptsize \rho=\displaystyle \frac{V}{m}[/latex]
- [latex]\scriptsize P=\rho \times g \times h[/latex]
- [latex]\scriptsize P=\displaystyle \frac{F}{A}[/latex]
- Air pressure at sea level is 14.5 pounds per square inch. Why do we not feel this pressure pushing on us?
- the amount is negligible to the feeling of gravity
- we have grown accustomed to it since we were born
- the fluids in our body are pushing outward with the same force
- the force of gravity negates the feeling of pressure
- The static fluid pressure at any given depth depends on:
- the total mass of the fluid
- the total volume of the fluid
- the surface area
- the distance below the surface
- all of the above
- In the equation for pressure [latex]\scriptsize P = \rho \times g \times h[/latex], the units for [latex]\scriptsize g[/latex] (SI system) are:
- [latex]\scriptsize \text{kg.m}^{-3}[/latex]
- [latex]\scriptsize \text{m.s}^{-1}[/latex]
- [latex]\scriptsize \text{kg.m.s}^{-1}[/latex]
- [latex]\scriptsize \text{m.s}^{-2}[/latex]
- What is the pressure at the bottom of a swimming pool that is 3 metres deep?
- [latex]\scriptsize (101\times 10^5) + (2.94\times 10^4)~\text{Pa}[/latex]
- [latex]\scriptsize (101\times 10^5) + (1.09 \times 10^5)~\text{Pa}[/latex]
- [latex]\scriptsize (101\times 10^5) + (3.63 \times 10^4)~\text{Pa}[/latex]
- [latex]\scriptsize (101\times 10^5) + (7 \times 10^4)~\text{Pa}[/latex]
- A pressure gauge is placed at the bottom of a reservoir of unknown depth. The reservoir contains water. If the pressure registered on the gauge is [latex]\scriptsize 126.578~\text{kPa}[/latex] and atmospheric pressure is [latex]\scriptsize 101.303~\text{kPa}[/latex], how deep is the reservoir?
- An open container of an unknown liquid is at sea level. A pressure gauge at a depth of [latex]\scriptsize 1.5~\text{m}[/latex] measures a pressure of [latex]\scriptsize 126.205~\text{kPa}[/latex]. What is the fluid density?
The full solutions are at the end of the unit.
Pascal’s principle
We ended the section above by noting that when a force is exerted on a fluid, this changes the pressure the fluid exerts and that this change in pressure is transmitted throughout the fluid. This is a simple statement of Pascal’s principle. This principle is the reason why a hydraulic jack can lift a car (see figure 6).

But how can a fluid be used to lift such heavy objects?
We know that pressure is defined as force per unit area. We also know that the pressure in a fluid can be increased by pushing directly on the fluid. This is how the heart pumps blood around our bodies. The key though is to have a closed system. If you try to push on a fluid in an open system, like a river, the fluid just flows away.
In an enclosed system, the fluid cannot flow away, and so the applied force can more easily result in an increase in pressure. When such a force is applied, the atoms in the fluid transmit the pressure to all parts of the fluid and to the walls of the container. Importantly, this change in pressure is transmitted undiminished (without any decrease).
This phenomenon is called Pascal’s principle. It states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
Take note!
Pascal’s principle states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
But we still don’t know how this change in pressure results in the ability to lift a car? Consider the system in figure 7. Here we have a closed system of two connected containers each with a stopper. Because they are connected, any change in pressure in one container will be transmitted undiminished through the whole system.
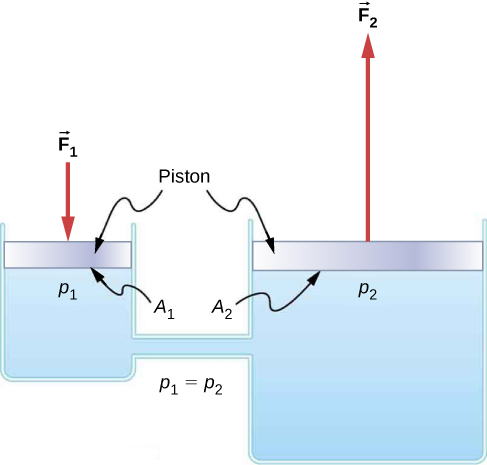
We know, therefore, that at all times [latex]\scriptsize P_1=P_2[/latex]. But we also know that:
[latex]\scriptsize P_1=\displaystyle \frac{F_1}{A_1}[/latex] and [latex]\scriptsize P_2=\displaystyle \frac{F_2}{A_2}[/latex].
Therefore:
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{A_1}&=\displaystyle \frac{F_2}{A_2}\\ \therefore \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2} \end{align*}[/latex]
Now if [latex]\scriptsize A_2 = 2A_1[/latex], this means that [latex]\scriptsize F_2=2F_1[/latex]. In other words, we will have doubled the force exerted by the liquid on the right-hand plunger in terms of the force we exerted on the left-hand plunger. We have a force multiplier. This simple hydraulic system has a mechanical advantage of two.
Note
Spend some time playing with the simple hydraulic system simulation called Pascal’s Principle in a Hydraulic Lift. Here you can change the radius of each plunger as well as the output force.
Example 1.4
In a car’s hydraulic brake system, a force of [latex]\scriptsize 500~\text{N}[/latex] is applied via the brake pedal, which acts on the master cylinder. The change in pressure created in the master cylinder is transmitted to each of the four slave cylinders at the wheels. If the master cylinder has a diameter of [latex]\scriptsize 0.500~\text{cm}[/latex], and each slave cylinder has a diameter of [latex]\scriptsize 2.50~\text{cm}[/latex], calculate the force created at each of the slave cylinders.
Solution
In a hydraulic system we know that [latex]\scriptsize \displaystyle \frac{F_1}{F_2}=\displaystyle \frac{A_1}{A_2}[/latex]. We need to first calculate the areas of the cylinders.
Master cylinder:
[latex]\scriptsize A=\pi r^2=\pi \times \left(0.25~\text{cm}\right)^2=0.0625~\text{cm}^2[/latex]
Slave cylinders:
[latex]\scriptsize A=\pi r^2=\pi \times \left(1.25~\text{cm}\right)^2=1.5625~\text{cm}^2[/latex]
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2}\\ \therefore F_2&=\displaystyle \frac{A_2}{A_1}\times F_1\\ &=\displaystyle \frac{1.5625~\text{cm}^2}{0.0625~\text{cm}^2} \times 500~\text{N}\\ &=1.25 \times 10^4~\text{N} \end{align*}[/latex]
Alternatively, we could have done the calculation as follows:
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2}\\ \therefore F_2&=\displaystyle \frac{A_2}{A_1}\times F_1\\ &=\displaystyle \frac{\pi r_2^2}{\pi r_1^2}\times F_1\\ &=\displaystyle \frac{\left(2.5~\text{cm}\right)^2}{\left(0.500~\text{cm}\right)^2} \times 500~\text{N}\\ &=1.25 \times 10^4~\text{N} \end{align*}[/latex]
Did you know?
Hydraulic systems are used for many applications. They are used in lift and crane systems, in the braking systems of motor vehicles, to operate the landing gear and wing flaps of aircraft and in many industrial robots.
Watch the video called Pascal Law | Hydraulic System and Pascal law | applications of pascal’s law.
Exercise 1.2
- What force must be exerted on the master cylinder of a hydraulic lift to support the weight of a [latex]\scriptsize 2~500~\text{kg}[/latex] car resting on a secondary cylinder? The master cylinder has a [latex]\scriptsize 2.00~\text{cm}[/latex] diameter and the secondary cylinder has a [latex]\scriptsize 25.0~\text{cm}[/latex] diameter.
- A certain hydraulic system is designed to exert a force [latex]\scriptsize 120[/latex] times as large as the one put into it.
- What must be the ratio of the area of the cylinder that is being controlled to the area of the master cylinder?
- What must be the ratio of their diameters?
- By what factor is the distance through which the output force moves reduced relative to the distance through which the input force moves? Assume no losses due to friction.
The full solutions are at the end of the unit.
Fluid pressure and velocity
So far in this unit, we have considered the pressure exerted by a fluid that is not moving. But fluids that are moving can also be under pressure and exert pressure. Indeed, it is differences in pressure that make a fluid move through a pipe in the first place – from high pressure to lower pressure.
However, it turns out that the thickness of the pipe affects both the pressure of the fluid and the velocity with which it flows in some surprising ways. Consider the case shown in figure 8.
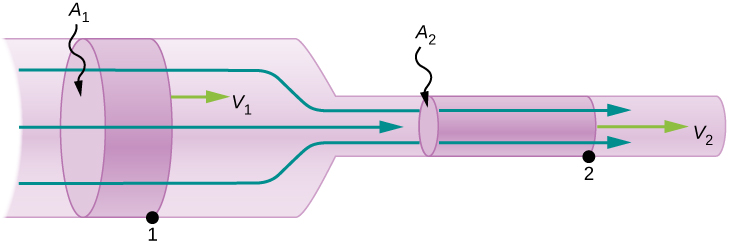
The first thing we need to note is that the same volume of fluid needs to flow through each part of the tube each second. Let’s assume that the shaded volume of fluid in the wide part of the tube flows past point 1 in one second. When this volume of fluid gets to the narrow part of the pipe, the same volume of fluid will have to flow past point 2 also in one second. However, we can see that, because the diameter of the tube has decreased, the length of this column of fluid needs to increase. This means that the velocity of the fluid needs to increase in order to get this ‘longer’ column of fluid past point 2 in one second.
So, as the diameter of a tube narrows, the velocity of the fluid flowing through that part of the tube increases.
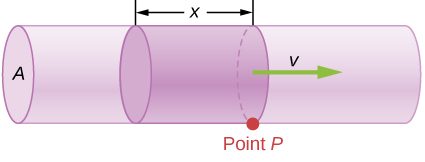
We call the volume of fluid flowing through a tube per unit time the flow rate ([latex]\scriptsize Q[/latex]). The SI units for flow rate are [latex]\scriptsize \text{m}^3\text{.s}^{-1}[/latex] but it is also commonly measured in [latex]\scriptsize \text{L.min}^{-1}[/latex]. The flow rate can be calculated as the cross-sectional area of the tube multiplied by the velocity of the fluid. In other words, [latex]\scriptsize Q=Av[/latex] (see figure 9).
Look back at figure 8. We know that the flow rate at point 1 must be equal to the flow rate at point 2. Therefore, we can say that if [latex]\scriptsize Q_1=Q_2[/latex] then [latex]\scriptsize A_1v_1=A_2v_2[/latex].
This is called the equation of continuity and is valid for any incompressible fluid with constant density. This can be seen when water flows from a hose. The smaller the diameter of the nozzle, the greater its velocity.
Example 1.5
A nozzle with a diameter of [latex]\scriptsize 0.5~\text{cm}[/latex] is attached to a high-pressure hose with a radius of [latex]\scriptsize 2~\text{cm}[/latex]. The flow rate through hose and nozzle is [latex]\scriptsize 0.6~\text{L.s}^{-1}[/latex]. Calculate the speed of the water:
- in the hose.
- in the nozzle.
Solutions
- We can use the concept of flow rate to calculate the velocity of the water through the hose.
[latex]\scriptsize \begin{align*} Q&=Av\\ \therefore v&=\displaystyle \frac{Q}{A}\\ &=\displaystyle \frac{0.6~\text{L.s}^{-1}\times 10^{-3}~\text{m}^3\text{.L}^{-1}}{\pi\left(0.01~\text{m}^2\right)}\\ &=1.91~\text{m.s}^{-1} \end{align*}[/latex] - We can use the equation of continuity to calculate the velocity of the water flowing through the nozzle.
[latex]\scriptsize \begin{align*} A_1v_1&=A_2v_2\\ \therefore v_2&=\displaystyle \frac{A_1}{A_2}\times v_1\\ &=\displaystyle \frac{\pi r_1^2}{\pi r_2^2}\times v_1\\ &=\displaystyle \frac{r_1^2}{r_2^2}\times v_1\\ &=\displaystyle \frac{\left(2~\text{cm}\right)^2}{\left(0.25~\text{cm}\right)^2}\times 1.91~\text{m.s}^{-1}\\ &=122.24~\text{m.s}^{-1} \end{align*}[/latex]
Now, what do you think happens to the pressure of the fluid as it flows through the narrow part of the tube in figure 8? Does its pressure increase or decrease? Spend a few moments thinking about this.
Watch the demonstration called Bernoulli’s Principle Demo: Venturi Tube so see what happens to the pressure of a fluid as it flows through a narrower part of a tube. The result may surprise you.
Did you see that as the velocity of the fluid increases through the narrower part of the tube, its pressure decreased? This is a simple statement of Bernoulli’s principle and is the fundamental reason that planes are able to fly.
Take note!
Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy.
Did you know?
Bernoulli’s principle is named after Daniel Bernoulli who published it in 1738. Leonhard Euler was the first to describe the principle in a mathematical equation in 1752. The Bernoulli equation is
[latex]\scriptsize P_1+\displaystyle \frac{1}{2}\rho v_1^2+\rho gh_1=P_2+\displaystyle \frac{1}{2}\rho v_2^2+\rho gh_2[/latex]
where:
[latex]\scriptsize P_1[/latex] and [latex]\scriptsize P_2[/latex] are the pressures at points 1 and 2
[latex]\scriptsize v_1[/latex] and [latex]\scriptsize v_2[/latex] are the velocities of the fluid at points 1 and 2
[latex]\scriptsize h_1[/latex] and [latex]\scriptsize h_2[/latex] is the height of points 1 and 2
[latex]\scriptsize \rho[/latex] is the density of the fluid
Notice how similar the [latex]\scriptsize \displaystyle \frac{1}{2}\rho v^2[/latex] parts of the expression are to that for kinetic energy [latex]\scriptsize \text{KE}=\displaystyle \frac{1}{2}mv^2[/latex]. Isn’t science amazing!
Watch the video called Venturi effect and Pitot tubes to see how we can use Bernoulli’s equation to prove that the greater the velocity of a fluid, the lower its pressure.
Exercise 1.3
- Calculate the time it would take to fill a public swimming pool with a capacity of [latex]\scriptsize 80~000~\text{L}[/latex] using a garden hose delivering [latex]\scriptsize 60~\text{L.min}^{-1}[/latex].
- Water is moving at a velocity of [latex]\scriptsize 2~\text{m.s}^{-1}[/latex] through a hose with an internal diameter of [latex]\scriptsize 1.60~\text{cm}[/latex].
- What is the flow rate in litres per second?
- The fluid velocity in this hose’s nozzle is [latex]\scriptsize 15~\text{m.s}^{-1}[/latex]. What is the nozzle’s inside diameter?
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- Density is mass per unit volume: [latex]\scriptsize \rho=\displaystyle \frac{m}{V}[/latex]
- The SI unit of density is [latex]\scriptsize \text{kg.m}^{-3}[/latex].
- Generally, solids are more dense than liquids and liquids are more dense than gases.
- Pressure is force divided by the perpendicular unit area: [latex]\scriptsize P=\displaystyle \frac{F}{A}[/latex]
- The SI unit of pressure is [latex]\scriptsize \text{Pa}[/latex].
- The pressure due to the weight of a fluid is given by [latex]\scriptsize P=h\rho g[/latex] where [latex]\scriptsize h[/latex] is the vertical height of the fluid above the point where the pressure is being measured, [latex]\scriptsize \rho[/latex] is the density of the fluid and [latex]\scriptsize g[/latex] is the acceleration due to gravity.
- The pressure at the bottom of a container of fluid exposed to the atmosphere is the sum of the pressure due to the weight of the fluid and the atmospheric pressure at the surface of the fluid.
- Pascal’s principle states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
- According to Pascal’s principle [latex]\scriptsize \displaystyle \frac{F_1}{F_2}=\displaystyle \frac{A_1}{A_2}[/latex].
- Flow rate ([latex]\scriptsize Q=[/latex]) is the volume of a fluid moving past a certain point per unit time. The SI units for flow rate are [latex]\scriptsize \text{m}^3\text{.s}^{-1}[/latex] but it is also commonly measured in [latex]\scriptsize \text{L.min}^{-1}[/latex].
- The flow rate can be calculated as the cross-sectional area of the tube multiplied by the velocity of the fluid: [latex]\scriptsize Q=Av[/latex]
- Bernoulli’s principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid’s potential energy.
- The relationship between fluid velocity and fluid pressure can be shown with a Venturi meter.
Unit 1: Assessment
Suggested time to complete: 45 minutes
Question 1 taken from Physical Science level 4 paper 2 March 2019 question 4
- A hydraulic press consists of two plungers A and B in contact with a liquid. The surface area of plunger A in contact with the liquid is [latex]\scriptsize 0.1~\text{m}^2[/latex] and the surface area of plunger B in contact with the liquid is [latex]\scriptsize 0.35~\text{m}^2[/latex], as shown in the sketch below. A force of [latex]\scriptsize 20~\text{N}[/latex] is applied to plunger A in order to hold a block of unknown mass stationary on plunger B.
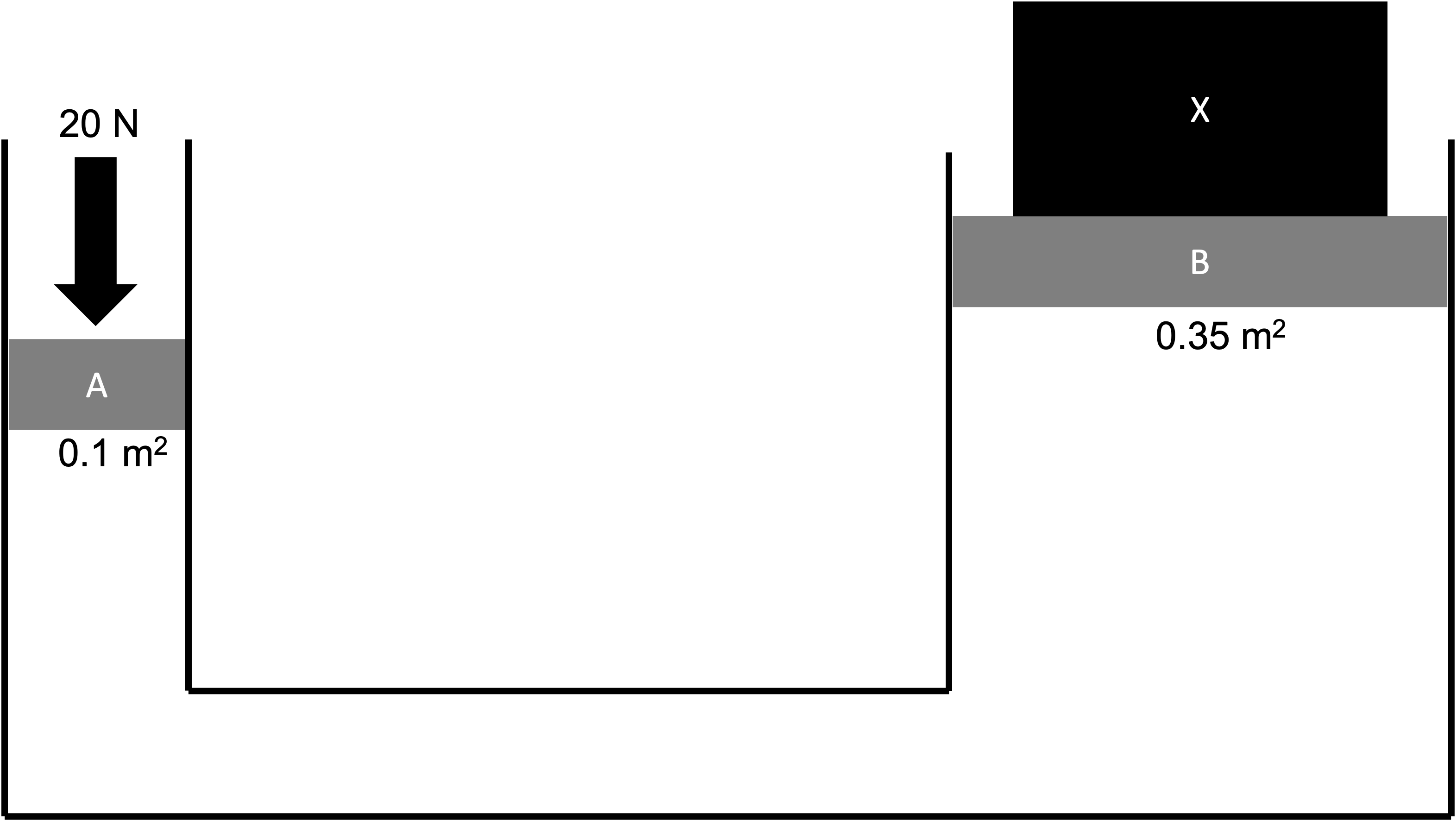
- Calculate the pressure exerted by plunger A on the surface of the liquid.
- Is the pressure exerted by the liquid on plunger B, greater than, equal to or less than the pressure exerted by plunger A on the liquid? Explain the answer with reference to a relevant scientific principle.
- Calculate the mass of block X.
- A host pours the remnants of several bottles of wine into a jug after a party and inserts a cork with a [latex]\scriptsize 2.00~\text{cm}[/latex] diameter into the bottle, placing it in direct contact with the wine. When the host hits the cork into place, the bottom of the jug (diameter [latex]\scriptsize 15~\text{cm}[/latex]) breaks away. Calculate the extra force exerted against the bottom if he hit the cork with a [latex]\scriptsize 100~\text{N}[/latex] force.
Question 3 taken from Physical Science level 4 paper 2 March 2019 question 4
- Water from a pipe of varying cross-sectional area flows into a circular steel tank. The cross-sectional area of the pipe at A is [latex]\scriptsize 0.08~\text{m}^2[/latex] and the speed of the water is [latex]\scriptsize 2~\text{m.s}^{-1}[/latex]. At B the cross-sectional area is [latex]\scriptsize 0.02~\text{m}^2[/latex]. The water completely fills the pipe at all times.
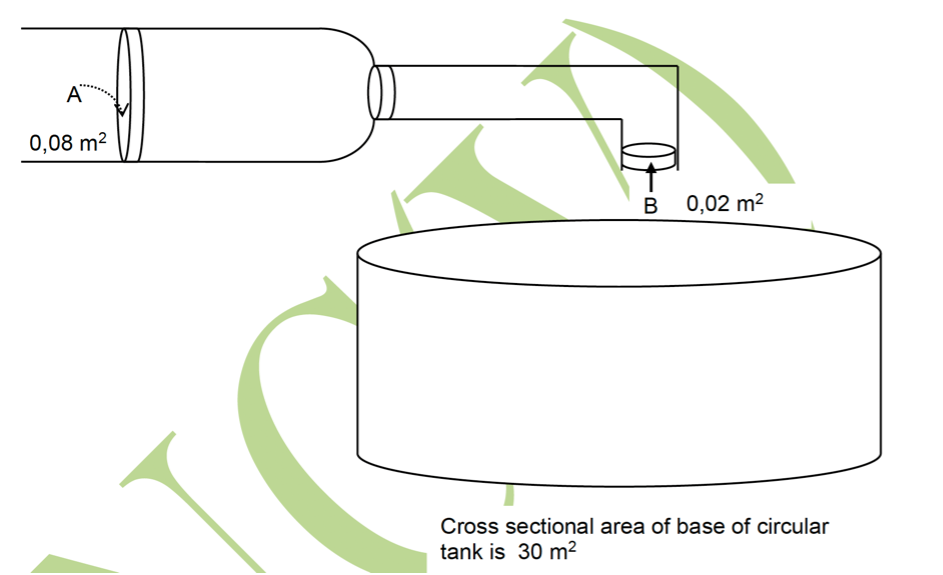
- Calculate the magnitude of the velocity of the water at B.
- What volume of water is ejected at B in 30 minutes?
- Determine the height of the water in the tank in 30 minutes.
- List two applications of Pascal’s principle.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- The equation in option b is incorrect: [latex]\scriptsize \rho=\displaystyle \frac{m}{V}[/latex]
- Option c is correct.
- Option d is correct: [latex]\scriptsize P=\rho gh[/latex]. The density of the fluid and the acceleration due to gravity are constant. Therefore, the pressure depends only on the depth [latex]\scriptsize h[/latex] or the distance below the surface.
- Option d is correct. The SI units for acceleration are [latex]\scriptsize \text{m.s}^{-2}[/latex].
- Option a is correct: [latex]\scriptsize P_{water}=\rho gh=1~000~\text{kg.m}^{-3}\times 9.8~\text{m.s}^{-2}\times 3~\text{m}=2.94\times 10^4~\text{Pa}[/latex]
- The pressure due to the weight of the water is:
[latex]\scriptsize 126.578~\text{kPa} - 101.303~\text{kPa}=25.275~\text{kPa}=25~275~\text{Pa}[/latex]
[latex]\scriptsize \begin{align*} P&=\rho gh\\ \therefore h&=\displaystyle \frac{P}{\rho g}\\ &=\displaystyle \frac{25~275~\text{Pa}}{1~000~\text{kg.m}^{3}\times 9.8~\text{m.s}^{-2}}\\ &=2.58~\text{m} \end{align*}[/latex] - Atmospheric pressure at sea level is [latex]\scriptsize 101.325~\text{kPa}[/latex]. Therefore, the pressure due to the weight of the fluid is:
[latex]\scriptsize 126.205~\text{kPa}-101.325~\text{kPa}=2~488~\text{Pa}[/latex]
[latex]\scriptsize \begin{align*} P&=\rho gh\\ \therefore \rho&=\displaystyle \frac{P}{gh}\\ &=\displaystyle \frac{2~488~\text{Pa}}{times 9.8~\text{m.s}^{-2}\times 1.5~\text{m}}\\ &=169.25~\text{kg.m}^{-3} \end{align*}[/latex]
Exercise 1.2
- .
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2}\\ \therefore F_1&=\displaystyle \frac{A_1}{A_2}F_2\\ &=\displaystyle \frac{\pi \left(1~\text{cm}\right)^2}{\pi \left(12.5~\text{cm}\right)^2}\times 24~500~\text{N}\\ &=156.8~\text{N} \end{align*}[/latex] - .
- If the ratio of input to output force is [latex]\scriptsize 1:120[/latex] then the ratio of the area of the input cylinder to the output cylinder must also be [latex]\scriptsize 1:120[/latex].
- The ratio of input cylinder diameter to the output cylinder diameter must be [latex]\scriptsize 1:\sqrt{120}[/latex].
- [latex]\scriptsize F_1\cdot d_1 = F_2 \cdot d_2[/latex]. If the ratio [latex]\scriptsize F_1:F_2 = 1:120[/latex], then the ratio [latex]\scriptsize d_1:d_2 = 120:1[/latex].
Exercise 1.3
- [latex]\scriptsize \displaystyle \frac{80~000~\text{L}}{60~\text{L.min}^{-1}}=1~333.33~\text{min}=22~\text{hrs and} 13~\text{min}[/latex].
- .
- .
[latex]\scriptsize \begin{align*} Q&=Av\\ &=\pi \left(0.8~\text{m}\right)^2 \times 2~\text{m.s}^{-1}\\ &=4.021~\text{m}^3\text{.s}^{-1}\\ &=4~021~\text{L.s}^{-1} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} A_1v_1&=A_2v_2\\ \therefore \displaystyle \frac{A_1}{A_2}&=\displaystyle \frac{v_2}{v_1}=\displaystyle \frac{15~\text{m.s}^{-1}}{2~\text{m.s}^{-1}}=7.5\\ \therefore \displaystyle \frac{\pi r_1^2}{\pi r_2^2}&=7.5\\ \therefore \displaystyle \frac{r_1^2}{r_2^2}&=7.5\\ \therefore r_2^2&=\displaystyle \frac{r_1^2}{7.5}\\ &=\displaystyle \frac{\left(0.8~\text{m}\right)^2}{7.5}\\ \therefore r_2&=\sqrt{\displaystyle \frac{\left(0.8~\text{m}\right)^2}{7.5}}\\ &=0.29~\text{m} \end{align*}[/latex]
- .
Unit 1: Assessment
- .
- [latex]\scriptsize P=\displaystyle \frac{F}{A}=\displaystyle \frac{20~\text{N}}{0.1~\text{m}^2}=200~\text{Pa}[/latex]
- The pressure is the same. Pascal’s principle states that a change in pressure applied to an enclosed fluid is transmitted undiminished to all portions of the fluid and to the walls of its container.
- .
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2}\\ \therefore F_2&=\displaystyle \frac{A_2}{A_1}F_1\\ &=\displaystyle \frac{0.35~\text{m}^2}{0.1~\text{m}^2}\times 20~\text{N}\\ &=70~\text{N}\\ F&=mg\\ \therefore m&=\displaystyle \frac{F}{g}\\ &=\displaystyle \frac{70~\text{N}}{9.8~\text{m.s}^{-2}}\\ &=7.14~\text{kg} \end{align*}[/latex]
- .
[latex]\scriptsize \begin{align*} \displaystyle \frac{F_1}{F_2}&=\displaystyle \frac{A_1}{A_2}\\ \therefore F_2&=\displaystyle \frac{A_2}{A_1}F_1\\ &=\displaystyle \frac{\pi \left(0.075~\text{m}\right)^2}{\pi \left(0.01~\text{m}\right)^2}\times 100~\text{N}\\ &=5~625~\text{N} \end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*} A_1v_1&=A_2v_2\\ \therefore v_2&=\displaystyle \frac{A_1}{A_2}v_1\\ &=\displaystyle \frac{0.08~\text{m}^2}{0.02~\text{m}^2}\times 2~\text{m.s}^{-1}\\ &=8~\text{m.s}^{-1} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} Q&=Av\\ &=0.02~\text{m}^2\times 8~\text{m.s}^{-1}\\ &=0.16~\text{m}^3\text{.s}^{-1}\\ 0.16~\text{m}^3\text{.s}^{-1}\times (30\times 60)~\text{s}&=288~\text{m}^3\\ &=288~000~\text{L} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} V&=A\times h\\ \therefore h&=\displaystyle \frac{V}{A}\\ &=\displaystyle \frac{288~\text{m}^3}{30~\text{m}^2}\\ &=9.6~\text{m} \end{align*}[/latex] - Hydraulic lifts and brakes systems for motor vehicles
- .
Media Attributions
- figure1 © Spirit469 is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure3 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure4 © Lumen Learning is licensed under a CC BY (Attribution) license
- activity1.1.1 © Phet is licensed under a CC BY (Attribution) license
- activity1.1.2 © Phet is licensed under a CC BY (Attribution) license
- figure5 is licensed under a CC0 (Creative Commons Zero) license
- Change engine oil and transmission inspection © SIGAUS is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure8 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure9 © Lumen Learning is licensed under a CC BY (Attribution) license
- assessmentQ1 © DHET is licensed under a CC BY (Attribution) license
- assessmentQ2 © DHET is licensed under a CC BY (Attribution) license
an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object
