Unit 2 outcomes

By the end of this unit you will be able to:

• Define Newton’s third law and identify examples of interacting objects that exert equal forces on each other.
• Define the law of conservation of momentum.
• Distinguish between elastic and inelastic collisions.
• Apply the law of conservation of momentum in calculations on different types of collisions.

What you should know

Before you start this unit, make sure you can:

• Define and calculate momentum. Refer to unit 1 if you need help with this.
• Calculate the change of momentum of an object.
• Define impulse as [latex]\scriptsize {{F}_{{nett}}}\cdot t[/latex] or [latex]\scriptsize \Delta p[/latex]. Refer to unit 1 if you need help with this.
• Understand kinetic energy. Refer back to level 2 subject outcome 2.3 if you need help with this.

Introduction

In the previous unit, we learnt how Isaac Newton viewed his second law of motion (normally expressed as [latex]\scriptsize {{F}_{{nett}}}=m\cdot a[/latex]) in terms of momentum, in other words that [latex]\scriptsize {{F}_{{nett}}}=\displaystyle \frac{{\Delta p}}{{\Delta t}}[/latex] or [latex]\scriptsize \Delta p={{F}_{{nett}}}\cdot \Delta t[/latex].

We defined [latex]\scriptsize \Delta p={{F}_{{nett}}}\cdot \Delta t[/latex] as impulse and looked at several situations where we calculated either the force or the time necessary to effect a specific change in momentum.

In many of these cases, we had two objects colliding with each other where the force exerted by object A on object B is equal and opposite to the force exerted by object B on object A. This is a simple statement of Newton’s third law of motion. But this has important consequences for momentum as we will see.

Newton’s third law of motion

You have probably heard the expression that ‘every action has an equal and opposite reaction’. This is a statement of Newton’s third law of motion. You have experienced this law of motion every time you hit your head on something. Your head applies a force to the object but the object applies an equal but opposite force to your head and it hurts!

Think about the case where two billiard balls collide (see figure 1).

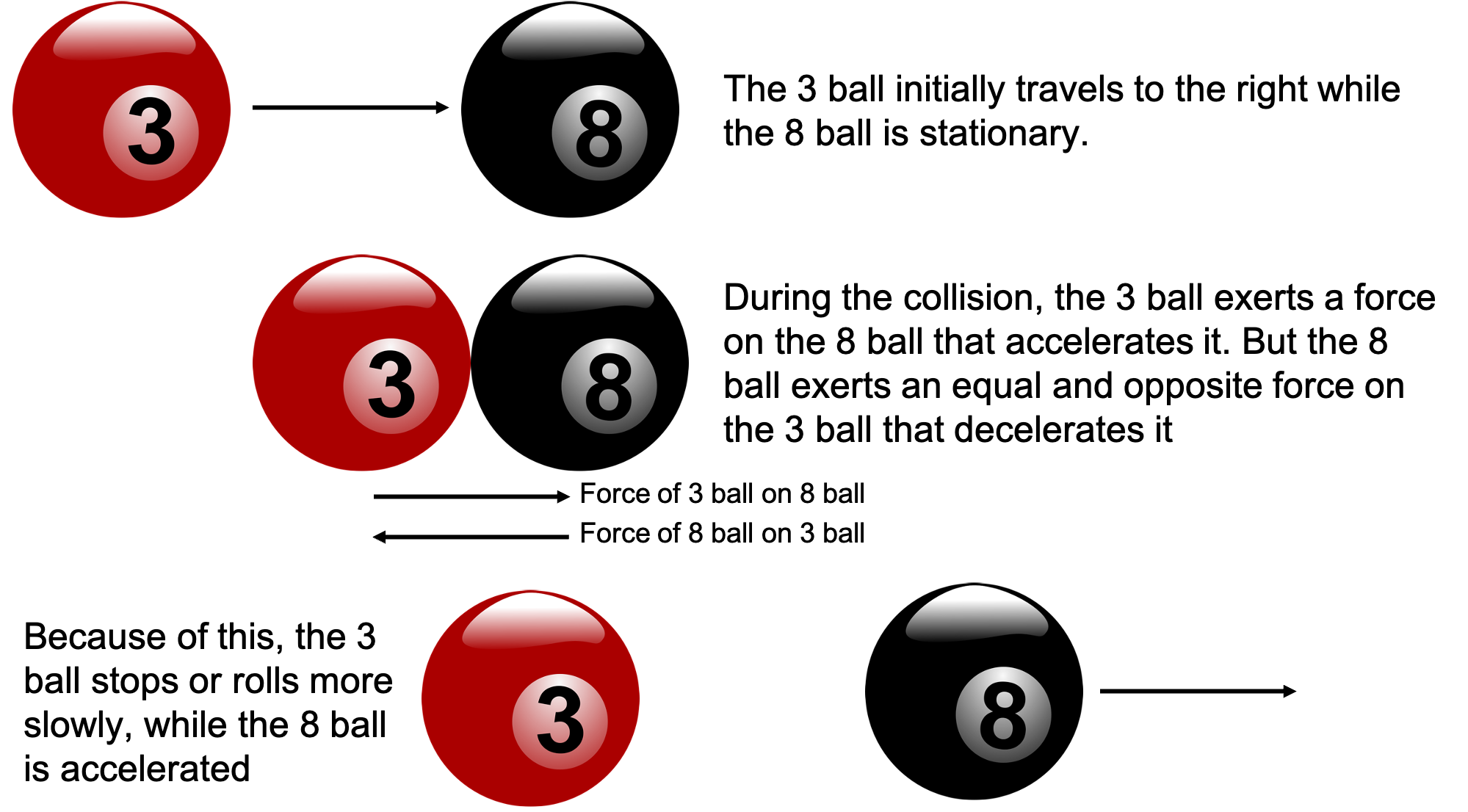
We can express the third law as [latex]\scriptsize {{F}_{{\text{3}\ \text{ball}}}}=-{{F}_{{\text{8 ball}}}}[/latex]. But we also know from the previous unit that [latex]\scriptsize {{F}_{{nett}}}=\displaystyle \frac{{\Delta p}}{{\Delta t}}[/latex]. Therefore, we can say that:

[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{{\Delta {{p}_{{\text{3 ball}}}}}}{{\Delta t}} & =-\displaystyle \frac{{\Delta {{p}_{{\text{8 ball}}}}}}{{\Delta t}}\\\therefore \Delta {{p}_{{\text{3 ball}}}} & =-\Delta {{p}_{{\text{8 ball}}}}\\\therefore \Delta {{p}_{{\text{3 ball}}}}+\Delta {{p}_{{\text{8 ball}}}} & =0\end{align*}[/latex]

This means that if you add up all the changes in momentum for an isolated system the net result will be zero. If we add up all the momenta in the system, the total momentum won’t change because the net change is zero.

The conservation of momentum

Another way of saying this is that, in a closed system, momentum is conserved or the total momentum before a collision (or explosion) is equal to the total momentum after a collision (or explosion). We can express this as [latex]\scriptsize {{P}_{{Ti}}}={{P}_{{Tf}}}[/latex].

The total momentum of the system before a collision is [latex]\scriptsize {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}[/latex] and the total momentum of the system after the collision is [latex]\scriptsize {{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}[/latex] (see figure 2).

This means that, where there are two colliding objects [latex]\scriptsize {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}[/latex]. The momentum of the isolated system is always conserved.

Let’s explore this further in the next two examples.

Example 2.1

In the situation illustrated in figure 1, the mass of each ball is [latex]\scriptsize 300\ \text{g}[/latex]. The 3 ball is initially moving at [latex]\scriptsize 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] to the right while the 8 ball is stationary.

1. What is the total momentum of the system before the collision?
2. If, after the collision, the 8 ball moves to the right at [latex]\scriptsize 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex], what is the velocity of the 3 ball?

Solutions

1. Step 1: Identify the information that has been given
   8 ball:
   [latex]\scriptsize {{v}_{{i8}}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. Therefore, [latex]\scriptsize {{p}_{{i8}}}=0\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].
   .
   3 ball:
   [latex]\scriptsize {{m}_{3}}=300\ \text{g}=0.3\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{{i3}}}=2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]to the right
   We define to the right as positive.
   .
   Step 2: Do the calculation
   [latex]\scriptsize {{p}_{{i3}}}={{m}_{3}}\times {{v}_{{i3}}}=0.3\ \text{kg}\times 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   The total momentum of the system will be the momentum of the 3 ball plus the momentum of the 8 ball.
   [latex]\scriptsize {{p}_{{Ti}}}={{p}_{{i3}}}+{{p}_{{i8}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}+0\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   Step 3: Write the final answer
   The total momentum of the system before the collision is [latex]\scriptsize 0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] to the right.
2. We know that the change in momentum of this closed or isolated system is zero. Therefore, the total momentum of the system before the collision will be equal to the total momentum of the system after the collision.
   
   Step 1: Identify the information that has been given
   [latex]\scriptsize {{p}_{{Ti}}}={{p}_{{Tf}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   [latex]\scriptsize {{v}_{{f8}}}=2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]to the right
   [latex]\scriptsize {{m}_{3}}=300\ \text{g}=0.3\ \text{kg}[/latex]
   .
   Step 2: Do the calculation
   [latex]\scriptsize \begin{align*}{{p}_{{f8}}} & =0.3\ \text{kg}\times 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\\\text{But}\ {{p}_{{Tf}}} & ={{p}_{{f8}}}+{{p}_{{f3}}}=0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\\\therefore {{p}_{{f3}}} & ={{p}_{{tf}}}-{{p}_{{f8}}}\\\therefore {{p}_{{f3}}} & =0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}-0.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}=0\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
   .
   [latex]\scriptsize \begin{align*}{{p}_{{f3}}}&={{m}_{3}}\times {{v}_{{f3}}}\\\therefore {{v}_{{f3}}}&=\displaystyle \frac{{{{p}_{{f3}}}}}{{{{m}_{3}}}}=\displaystyle \frac{{0\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.3\ \text{kg}}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
   .
   Step 3: Write the final answer
   The 3 ball will move at [latex]\scriptsize 0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] immediately after the collision. It will be stationary.

Example 2.2

Example adapted from Everything Science Grade 12 Worked example 9 page 42

A jet flies at a speed of [latex]\scriptsize 275\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] relative to the ground. The pilot fires a missile forward off a mounting at a speed of [latex]\scriptsize 700\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] relative to the ground. The respective masses of the jet and the missile are [latex]\scriptsize 5\ 000\ \text{kg}[/latex] and [latex]\scriptsize 50\ \text{kg}[/latex].

Treating the system as an isolated system, calculate the new speed of the jet immediately after the missile was fired.

Solution

Step 1: Identify the information that has been given
Let the plane be object 1 and the missile object 2. Define the initial direction of the plane as positive.

[latex]\scriptsize {{m}_{1}}=5\ 000\ \text{kg}[/latex]
[latex]\scriptsize {{v}_{{i1}}}=275\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
[latex]\scriptsize {{m}_{2}}=50\ \text{kg}[/latex]
[latex]\scriptsize {{v}_{{i2}}}={{v}_{{i1}}}=275\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] (the missile and plane are travelling at the same speed)
[latex]\scriptsize {{v}_{{f2}}}=700\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
We need to find the final speed of the plane ([latex]\scriptsize {{v}_{{f1}}}[/latex]) and we can use the conservation of momentum because we can treat it as an isolated system.

Step 2: Do the calculation
[latex]\scriptsize \begin{align*}{{p}_{i}} & ={{p}_{f}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{fi}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\But\ {{v}_{{i2}}} & ={{v}_{{i1}}}\\\therefore ({{m}_{1}}+{{m}_{2}})\cdot {{v}_{{i1}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{f1}}} & =({{m}_{1}}+{{m}_{2}})\cdot {{v}_{{i1}}}-{{m}_{2}}\cdot {{v}_{{f2}}} & \\\therefore {{v}_{{f1}}} & =\displaystyle \frac{{({{m}_{1}}+{{m}_{2}})\cdot {{v}_{{i1}}}-{{m}_{2}}\cdot {{v}_{{f2}}}}}{{{{m}_{1}}}} & \\\therefore {{v}_{{f1}}} & =\displaystyle \frac{{(5\ 000\ \text{kg}+50\ \text{kg})\times 275\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-(50\ \text{kg}\times 700\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{5\ 000\ \text{kg}}}\\ & =270.75\ m.{{s}^{{-1}}}\end{align*}[/latex]

Step 3: Write the final answer
The plane’s velocity after firing the missile is [latex]\scriptsize 270.75\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in its initial direction.

Exercise 2.1

1. A [latex]\scriptsize 70\ \text{ton}[/latex] train is travelling north at a velocity of [latex]\scriptsize 40\ \text{km/h}[/latex] when it is approached by a [latex]\scriptsize 50\ \text{ton}[/latex] train travelling south at a velocity of [latex]\scriptsize 55\ \text{km/h}[/latex] in the opposite direction. Calculate the total momentum of the system.
2. A bullet of mass [latex]\scriptsize 55\text{ g}[/latex] travelling horizontally at [latex]\scriptsize 540\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] hits a stationary target of mass [latex]\scriptsize 3.5\ \text{kg}[/latex] resting on a smooth horizontal surface. The bullet goes through the target and comes out on the other side at [latex]\scriptsize 225\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. Calculate the velocity of the target after the bullet has come out the other side. Assume that the target experiences no friction in its motion.

The full solutions can be found at the end of the unit.

Elastic collisions

Have a look at example 2.1 again. Here we had two billiard balls colliding. We were told that each ball has a mass of [latex]\scriptsize 300\ \text{g}[/latex] and that initially the 3 ball rolled to the right at [latex]\scriptsize 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] while the 8 ball was stationary. After the collision, the 8 ball moved to the right with a velocity of [latex]\scriptsize 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] and we calculated, because of the conservation of momentum, that the 3 ball would move to the right with a velocity of [latex]\scriptsize 0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] (see figure 3).

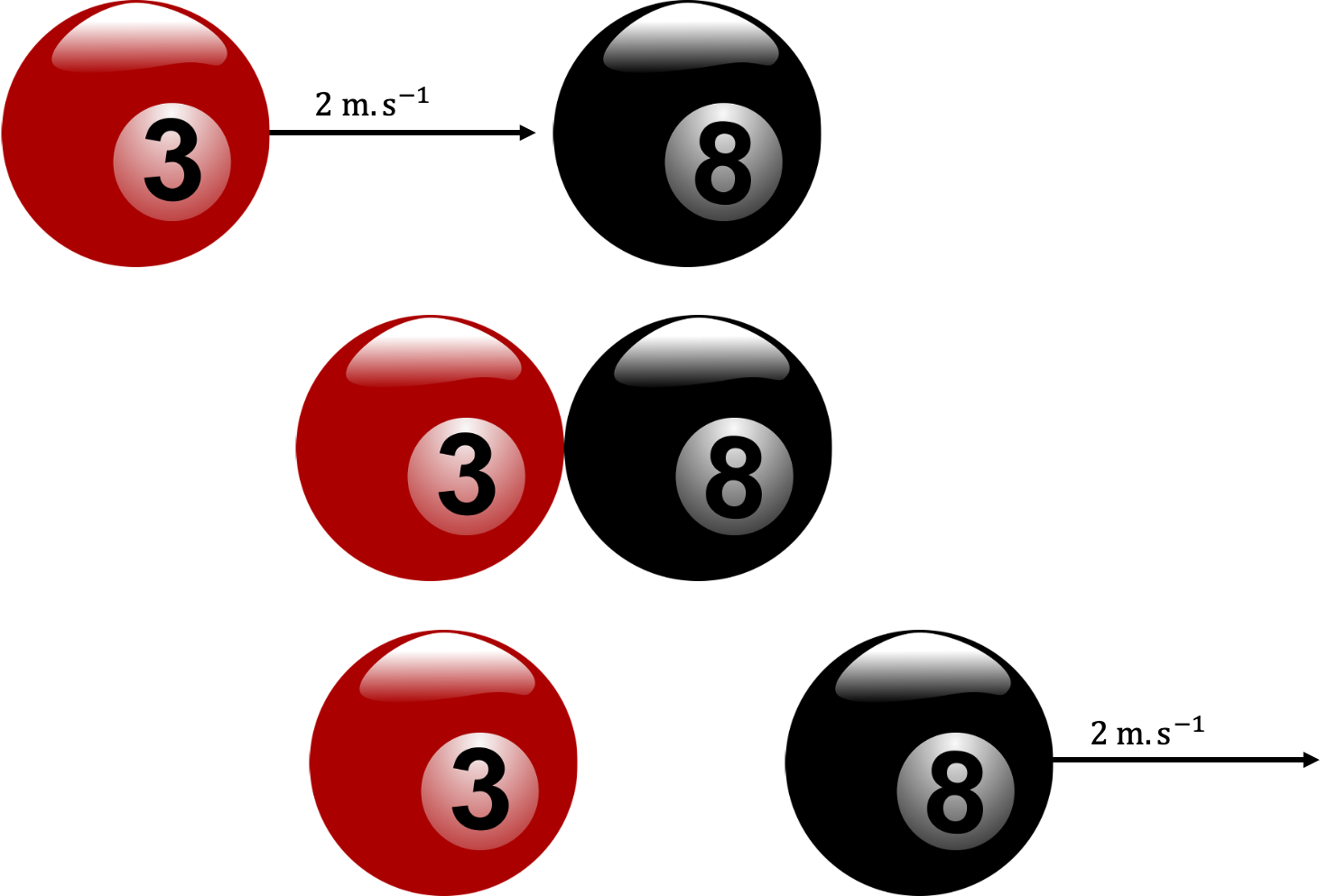
We know that momentum in this isolated system is conserved. But what else is conserved? Have a look at figure 3 to see if you can see what this is.

The mass of the balls is the same. We also know that billiard balls are made to transfer kinetic energy very effectively from one ball to the other. Can you see that the total kinetic energy before the collision is the same as the total kinetic energy after the collision?

Before the collision:
[latex]\scriptsize K{{E}_{{i3}}}=\displaystyle \frac{1}{2}\times {{m}_{3}}\times {{v}_{{i3}}}^{2}=\displaystyle \frac{1}{2}\times 0.3\ \text{kg}\times {{\left( {2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}=0.6\ \text{J}[/latex]
[latex]\scriptsize \displaystyle K{{E}_{{i8}}}=\displaystyle \frac{1}{2}\times {{m}_{8}}\times {{v}_{{i8}}}^{2}=\displaystyle \frac{1}{2}\times 0.3\ \text{kg}\times {{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}=0\ \text{J}[/latex]

[latex]\scriptsize K{{E}_{{Ti}}}=0.6\ \text{J}[/latex]

After the collision:
[latex]\scriptsize K{{E}_{{f3}}}=\displaystyle \frac{1}{2}\times {{m}_{3}}\times {{v}_{{f3}}}^{2}=\displaystyle \frac{1}{2}\times 0.3\ \text{kg}\times {{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}=0\ \text{J}[/latex]
[latex]\scriptsize \displaystyle K{{E}_{{f8}}}=\displaystyle \frac{1}{2}\times {{m}_{8}}\times {{v}_{{f8}}}^{2}=\displaystyle \frac{1}{2}\times 0.3\ \text{kg}\times {{\left( {2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}=0.6\ \text{J}[/latex]

[latex]\scriptsize K{{E}_{{Tf}}}=0.6\ \text{J}[/latex]

This is an example of an elastic collision. This is a collision where the total momentum of the isolated system is conserved AND the total kinetic energy of the isolated system is conserved (see figure 4).

Take note!

In an elastic collision:

• total momentum is conserved:
  [latex]\scriptsize \begin{align*}{{p}_{i}} & ={{p}_{f}}\\\therefore {{p}_{{i1}}}+{{p}_{{i2}}} & ={{p}_{{f1}}}+{{p}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\end{align*}[/latex]
• total kinetic energy is conserved:
  [latex]\scriptsize \begin{align*}E{{K}_{i}} & =E{{K}_{f}}\\\therefore E{{K}_{{i1}}}+E{{K}_{{i2}}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}\\\therefore \displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2} & =\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\end{align*}[/latex]

Example 2.3

Two marbles collide. Marble 1 has mass [latex]\scriptsize 30\ \text{g}[/latex] and marble 2 has mass [latex]\scriptsize 60\ \text{g}[/latex].

Marble 1 rolls to the right with an initial velocity of [latex]\scriptsize 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. Marble 2 is initially at rest. After they collide, both marbles are moving.

1. What is the final velocity of marble 1 if marble 2 has a velocity of [latex]\scriptsize 1.8\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] to the right?
2. Is this an elastic collision?

Solutions

1. Step 1: Identify the information that has been given
   [latex]\scriptsize {{m}_{1}}=30\ \text{g}=0.03\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{{i1}}}=2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] to the right
   [latex]\scriptsize \displaystyle {{m}_{2}}=60\ \text{g}=0.06\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{{i2}}}=1.8\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   [latex]\scriptsize {{v}_{{f2}}}=1.1\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   Define movement to the right as positive.
   .
   Step 2: Do the calculation
   Momentum conserved:
   [latex]\scriptsize \begin{align*} {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\ \text{But}\ {{v}_{{i2}}} & =0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\ \therefore {{m}_{1}}\cdot {{v}_{{i1}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\ \therefore {{m}_{1}}\cdot {{v}_{{f1}}} & ={{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{2}}\cdot {{v}_{{f2}}}\\ \therefore {{v}_{{f1}}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{1}}\cdot {{v}_{{f2}}}}}{{{{m}_{1}}}}\\ &=\displaystyle \frac{0.003\ \text{kg}\times 2.5\ \text{m} \text{.}{\text{s}}^{\text{-1}}-0.06\ \text{kg}\times 1.1\ \text{m} \text{.}{\text{s}}^{\text{-1}}}{0.03\ \text{kg}}\\ &=0.3\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}} \end{align*}[/latex]
   .
   Step 3: Write the final answer
   Marble 1 will have a final velocity of [latex]\scriptsize 0.3\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]to the right.
2. To determine if the collision is elastic we need to determine if kinetic energy is conserved.
   [latex]\scriptsize \begin{align*}E{{K}_{i}} & =\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\times 0.03\ \text{kg}\times {{\left( {2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}+\displaystyle \frac{1}{2}\times 0.06\ \text{kg}\times {{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}\\&=0.09375\ \text{J}\end{align*}[/latex][latex]\scriptsize \begin{align*}E{{K}_{f}} & =\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\\&=\displaystyle \frac{1}{2}\times 0.03\ \text{kg}\times {{\left( {0.3\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}+\displaystyle \frac{1}{2}\times 0.06\ \text{kg}\times {{\left( {1.1\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}\\&=0.00135\ \text{J}+0.0363\ \text{J}\\&=0.03765\ \text{J}\end{align*}[/latex]
   [latex]\scriptsize E{{K}_{i}}\ne E{{K}_{f}}[/latex]. Therefore, the collision is not elastic.

Take note!

If you are asked to prove that a collision is elastic, you need to show that the total kinetic energy before the collision is equal to the total kinetic energy after the collision.

Inelastic collisions

In reality, however, most collisions are not elastic. In fact, the only perfectly elastic collisions that occur in the real world are those between some sub-atomic particles. In all other cases, the collisions result in some loss of kinetic energy in the form of sound, heat, and the permanent deformation of the objects in question.

Figure 5 shows an example of this. In this head on collision between these two cars, it is clear that they did not bounce off each other like billiard balls! Most of the initial kinetic energy before the collision was converted to sound, heat, and the energy necessary to permanently deform the cars. The force needed to damage the cars was available because of the conservation of momentum. Remember that in all collisions, momentum is always conserved.

Figure 5: A non-elastic collision

Another example of an inelastic collision is a meteor crashing into the earth and forming an impact crater (see figure 6). In this kind of collision, the initial kinetic energy of the meteor is definitely not conserved as kinetic energy. Instead, it results in so much heat being generated, that the meteor and the earth’s surface is largely melted or vapourised and a huge crater in the surface of the earth is formed.

Figure 6: An impact crater

Take note!

In an inelastic collision:

• total momentum is conserved:
  [latex]\scriptsize \begin{align*}{{p}_{i}} & ={{p}_{f}}\\\therefore {{p}_{{i1}}}+{{p}_{{i2}}} & ={{p}_{{f1}}}+{{p}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\end{align*}[/latex]
• total kinetic energy is not conserved:
  [latex]\scriptsize E{{K}_{i}}\ne E{{K}_{f}}[/latex]

Example 2.4

A truck and a car are involved in a head on collision. The car is initially travelling at [latex]\scriptsize 65\ \text{km/h}[/latex] east while the truck is travelling at [latex]\scriptsize 30\ \text{km/h}[/latex] west. The truck has a mass of [latex]\scriptsize \displaystyle 3.5\ \text{tons}[/latex] while the car has a mass of [latex]\scriptsize 850\ \text{kg}[/latex]. After colliding inelastically, the truck and the car stick together. What is the resulting velocity of the mass of metal formed?

Solution

Step 1: Identify the information that has been given
Let the truck be object 1 and the car be object 2.
Define west as positive
[latex]\scriptsize \displaystyle {{m}_{1}}=3.5\ \text{tons}=3\ 500\ \text{kg}[/latex]
[latex]\scriptsize {{v}_{{i1}}}=30\ \text{km/h}=8.33\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]west
[latex]\scriptsize \displaystyle {{m}_{2}}=850\ \text{kg}[/latex]
[latex]\scriptsize {{v}_{{i2}}}=65\ \text{km/h}=18.06\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]east
The truck and the car become one mass after the collision. Therefore, [latex]\scriptsize {{v}_{{f1}}}={{v}_{{f2}}}={{v}_{f}}[/latex].
We need to calculate the velocity of the car and truck mass.
Momentum is conserved.

Step 2: Do the calculation
[latex]\scriptsize \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}& ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{v}_{f}}\cdot ({{m}_{1}}+{{m}_{2}})\\\therefore {{v}_{f}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}}}{{({{m}_{1}}+{{m}_{2}})}}\\&=\displaystyle \frac{{3\ 500\ \text{kg}\times 8.33\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+850\ \text{kg}\times (-18.06\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{3\ 500\ \text{kg}+850\ \text{kg}}}\\&=3.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]

Step 3: Write the final answer
The final velocity of the truck and car mass is [latex]\scriptsize 3.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] west.

Take note!

If you are asked to prove that a collision is inelastic, you need to show that the total kinetic energy before the collision is not equal to the total kinetic energy after the collision.

Exercise 2.2

Question 1 adapted from Everything Science Grade 12 Exercise 2 – 4 question 1

1. A truck of mass [latex]\scriptsize 4\ 500\ \text{kg}[/latex] travelling at [latex]\scriptsize 20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] hits a car from behind. The car (mass [latex]\scriptsize 1\ 000\ \text{kg}[/latex]) is travelling at [latex]\scriptsize 15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. The two vehicles, now connected, carry on moving together.
   1. Calculate the final velocity of the truck-car combination after the collision.
   2. Determine the kinetic energy of the system before and after the collision.
   3. Explain the difference in your answers for b.
   4. Was this an example of an elastic or inelastic collision? Give reasons for your answer.
2. Two billiard balls each with a mass of [latex]\scriptsize 200\ \text{g}[/latex] collide head-on in an elastic collision. The 4 ball was travelling at a velocity of [latex]\scriptsize 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] and the 2 ball at a velocity of [latex]\scriptsize 1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. After the collision, the 4 ball travels away from the 2 ball at a velocity of [latex]\scriptsize 1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].
   1. Calculate the velocity of the 2 ball after the collision.
   2. Prove that the collision was elastic, showing all calculations.

The full solutions can be found at the end of the unit.

Summary

In this unit you have learnt the following:

• Newton’s third law of motion states that every action has an equal and opposite reaction. In other words, if object A exerts a force on object B, then object B will exert an equal but opposite force on object A.
• Momentum is conserved. This means that the momentum of any isolated system is constant or the change in momentum of an isolated system is zero or the total momentum before a collision is equal to the total momentum after a collision.
• In elastic collisions kinetic energy is conserved or the kinetic energy before a collision is equal to the kinetic energy after a collision.
• In inelastic collisions kinetic energy is not conserved. The kinetic energy before a collision is not equal to the kinetic energy after a collision.

Unit 2: Assessment

Suggested time to complete: 15 minutes

Question 1 adapted from Everything Science Grade 12 Worked example 18 page 59

1. A thief is driving at [latex]\scriptsize 40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east to evade the police. The thief’s car has a mass of [latex]\scriptsize 1\ 000\ \text{kg}[/latex]. The thief’s car collides head-on with a truck of mass [latex]\scriptsize 5\ 000\ \text{kg}[/latex] moving at [latex]\scriptsize 20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the opposite direction. After the collision, the car and the truck move together. Ignore the effects of friction.
   1. State the law of conservation of linear momentum in words.
   2. Calculate the velocity of the thief’s car immediately after the collision.
   3. Research has shown that forces greater than [latex]\scriptsize \text{85}\ 000\ \text{N}[/latex] during collisions may cause fatal injuries. The collision described above lasts for [latex]\scriptsize 0.5\ \text{s}[/latex]. Determine, by means of a calculation, whether the collision above could result in a fatal injury.

Question 2 adapted from NC(V) Physical Science Level 4 November 2015 Paper 1 question 7.2

2. The figure shows a car with a mass of [latex]\scriptsize 1\ 000\ \text{kg}[/latex] that moves along a horizontal road at [latex]\scriptsize 20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] west. It collides with a taxi of mass [latex]\scriptsize 1\ 500\ \text{kg}[/latex] moving along the same horizontal road at [latex]\scriptsize 25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east. The two vehicles join together upon collision.
   
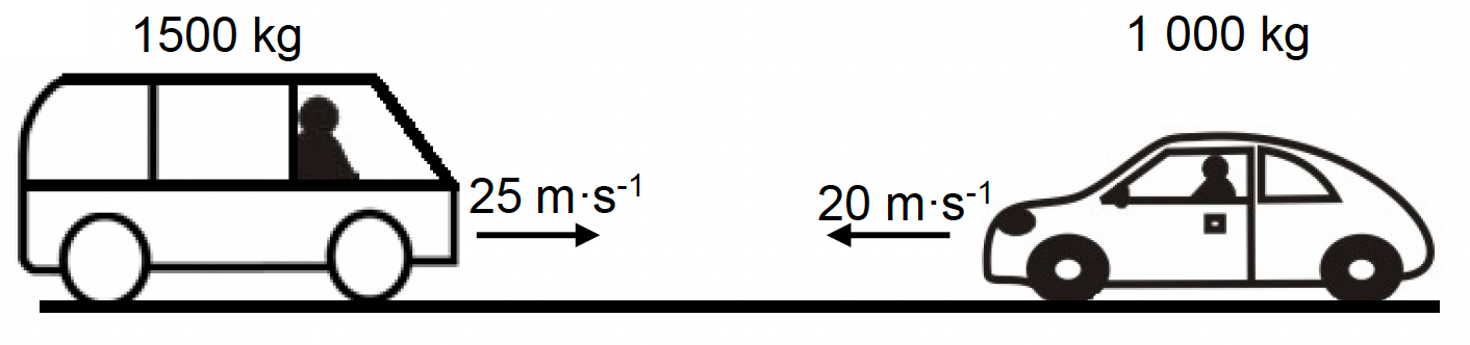
   1. Calculate the velocity of the car after collision.
   2. A learner says that the force that the car and the taxi experience during collision will be the same. Is the learner correct? Explain the answer in terms of the relevant law of physics.
   3. Calculate the impulse experienced by the taxi.
   4. Is the collision elastic or inelastic? Show by means of a calculation how you arrived at the answer.

Question 3 adapted from NC(V) Physical Science Level 4 November 2019 Paper 1 question 7

3. An object of mass [latex]\scriptsize 3\ \text{kg}[/latex], moving at [latex]\scriptsize 6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex], collides with a stationary object of mass [latex]\scriptsize 6\ \text{kg}[/latex]. The [latex]\scriptsize 3\ \text{kg}[/latex] object rebounds after the collision with a speed of [latex]\scriptsize 2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].
   1. Calculate the speed of the [latex]\scriptsize 6\ \text{kg}[/latex] object after collision.
   2. Show by means of a calculation whether the collision is elastic or inelastic.
4. In a railway shunting yard, a locomotive of mass [latex]\scriptsize 4\ 500\ \text{kg}[/latex], travelling north at a velocity of [latex]\scriptsize 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex], collides with a stationary goods wagon of mass [latex]\scriptsize 7\ 000\ \text{kg}[/latex] in an attempt to couple with it. The coupling fails and instead the goods wagon moves north with a velocity of [latex]\scriptsize 1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].
   1. Calculate the magnitude and direction of the velocity of the locomotive immediately after collision.
   2. Name and state in words the law you used to answer the previous question.
   3. Was the collision inelastic or not? Show your calculations.
   4. If the coupling had been successful, what would the locomotive’s velocity have been immediately after the collision?

The full solutions can be found at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. Let train travelling north be 1 and train travelling south be 2.
   [latex]\scriptsize {{m}_{1}}=70\ \text{ton}=70\ 000\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{1}}=40\ \text{km/h}=11.11\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north
   [latex]\scriptsize {{m}_{2}}=50\ \text{ton}=50\ 000\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{2}}=55\ \text{km/h}=15.28\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] south
   Let north be positive.
   We need to calculate the total momentum.
   .
   [latex]\scriptsize \begin{align*}{{p}_{T}} & ={{p}_{1}}+{{p}_{2}}\\&={{m}_{1}}\cdot {{v}_{1}}+{{m}_{2}}\cdot {{v}_{2}}\\&=70\ 000\ \text{kg}\times 11.11\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+50\ 000\ \text{kg}\times (-15.28\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})\\&=13\ 700\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
   The total momentum is [latex]\scriptsize 13\ 700\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north.
2. Let the bullet be object 1 and target be object 2.
   [latex]\scriptsize {{m}_{1}}=55\ \text{g}=0.055\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{{i1}}}=540\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   [latex]\scriptsize {{v}_{{f1}}}=225\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   [latex]\scriptsize {{m}_{2}}=3.5\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{{i2}}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   Let the bullet’s initial direction be positive.
   .
   [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\text{But}\ {{v}_{{i2}}} & =0\ m.{{s}^{{-1}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{2}}\cdot {{v}_{{f2}}} & ={{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{1}}\cdot {{v}_{{f1}}}\\\therefore {{v}_{{f2}}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{1}}\cdot {{v}_{{f1}}}}}{{{{m}_{2}}}}\\\therefore {{v}_{{f2}}} & =\displaystyle \frac{{{{m}_{1}}\cdot ({{v}_{{i1}}}-{{v}_{{f1}}})}}{{{{m}_{2}}}}\\&=\displaystyle \frac{{0.055\ \text{kg}\times (540\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-225\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{3.5\ \text{kg}}}\\&=4.95\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
   The block’s velocity will be [latex]\scriptsize 4.95\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the direction of the bullet.

Back to Exercise 2.1

Exercise 2.2

1. .
   1. Let the truck be object 1 and the car be object 2.
      Let the initial direction of the truck and car be positive.
      [latex]\scriptsize {{m}_{1}}=4\ 500\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{m}_{2}}=1\ 000\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{{f1}}}={{v}_{{f2}}}={{v}_{f}}[/latex]
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} &={{v}_{f}}\cdot ({{m}_{1}}+{{m}_{2}})\\\therefore {{v}_{f}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}}}{{({{m}_{1}}+{{m}_{2}})}}\\&=\displaystyle \frac{{4\ 500\ \text{kg}\times 20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+1\ 000\ \text{kg}\times \text{15}\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{4\ 500\ \text{kg}+1\ 000\ \text{kg}}}\\&=19.09\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The final velocity of the truck and car is [latex]\scriptsize 19.09\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the initial direction of the vehicles.
   2. .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{i}} & =E{{K}_{{i1}}}+E{{K}_{{i2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {4\ 500\ \text{kg}\times {{{\left( {20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+1\ 000\ \text{kg}\times {{{\left( {\text{15}\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=1\ 012\ 500\ \text{J}\end{align*}[/latex]
      .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{f}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\\\text{But}\ {{v}_{{f1}}} & ={{v}_{{f2}}}={{v}_{f}}\\\therefore E{{K}_{f}} & =\displaystyle \frac{1}{2}\cdot {{v}_{f}}^{2}\left( {{{m}_{1}}+{{m}_{2}}} \right)\\&=\displaystyle \frac{1}{2}\times {{\left( {19.09\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}^{2}}\times \left( {4\ 500\ \text{kg}+1\ 000\ \text{kg}} \right)\\&=1\ 002\ 177.28\ \text{J}\end{align*}[/latex]
   3. The total kinetic energy after the collision is less than before the collision. This is because some of the kinetic energy was converted into sound and heat and was used up in the permanent deformation of both the truck and car.
   4. This was an inelastic collision because the kinetic energy of the system was not conserved.
2. .
   1. Let the 4 ball be object 1 and the 2 ball be object 2.
      [latex]\scriptsize {{m}_{1}}=200\ \text{g}=0.2\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{m}_{2}}=200\ \text{g}=0.2\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{{f1}}}=1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      Momentum and kinetic energy are conserved.
      Define the initial direction of 4 ball as positive.
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{2}}\cdot {{v}_{{f2}}} & ={{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}-{{m}_{1}}\cdot {{v}_{{f1}}}\\\therefore {{v}_{{f2}}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}-{{m}_{1}}\cdot {{v}_{{f1}}}}}{{{{m}_{2}}}}\\&=\displaystyle \frac{{0.2\ \text{kg}\times 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+0.2\ \text{kg}\times (-1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})-0.2\ \text{kg}\times (-1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{0.2\ \text{kg}}}\\&=2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The 2 ball will travel at [latex]\scriptsize 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the initial direction of the 4 ball.
   2. .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{i}} & =E{{K}_{{i1}}}+E{{K}_{{i2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {0.2\ \text{kg}\times {{{\left( {2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+0.2\ \text{kg}\times {{{\left( {-1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=0.85\ \text{J}\end{align*}[/latex]
      .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{f}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {0.2\ \text{kg}\times {{{\left( {-1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+0.2\ \text{kg}\times {{{\left( {\text{2}\text{.5}\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=0.85\ \text{J}\end{align*}[/latex]
      Therefore, [latex]\scriptsize E{{K}_{i}}=E{{K}_{f}}[/latex]. Kinetic energy was conserved and so the collision was elastic.

Back to Exercise 2.2

Unit 2: Assessment

1. .
   1. The total momentum of an isolated system before a collision is equal to the total momentum of the system after a collision, or the total momentum of an isolated system is constant, or the total change in momentum of an isolated system is zero.
   2. Let the thief’s car be object 1 and the truck be object 2.
      [latex]\scriptsize {{m}_{1}}=1\ 000\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east
      [latex]\scriptsize {{m}_{2}}=5\ 000\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] west
      [latex]\scriptsize {{v}_{{f1}}}={{v}_{{f2}}}={{v}_{f}}[/latex]
      Define east as positive.
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} &={{v}_{f}}\cdot ({{m}_{1}}+{{m}_{2}})\\\therefore {{v}_{f}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}}}{{({{m}_{1}}+{{m}_{2}})}}\\&=\displaystyle \frac{{1\ 000\ \text{kg}\times 40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+5\ 000\ \text{kg}\times (-20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{1\ 000\ \text{kg}+5\ 000\ \text{kg}}}\\&=-10\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The velocity of the car and truck after the collision is [latex]\scriptsize 10\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] west.
   3. Occupants of the car:
      [latex]\scriptsize \displaystyle \begin{align*}\Delta p & ={{m}_{1}}\cdot {{v}_{{f1}}}-{{m}_{1}}\cdot {{v}_{{i1}}}\\&=1\ 000\ \text{kg}\times (-10\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})-1\ 000\ \text{kg}\times 40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\&=-50\ 000\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}{{F}_{{nett}}} & =\displaystyle \frac{{\Delta p}}{{\Delta t}}\\&=\displaystyle \frac{{-50\ 000\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.5\ \text{s}}}\\&=-100\ 000\ \text{N}\end{align*}[/latex]
      The occupants of the car would be subject to a force of [latex]\scriptsize 100\ 000\ \text{N}[/latex]. Therefore, the collision could result in a fatal injury for the occupants of the car. The occupants of the truck would be subject to an equal and opposite force. Therefore, the collision could result in a fatal injury for the occupants of the truck as well.
2. .
   1. Let the car be object 1 and the taxi be object 2.
      [latex]\scriptsize {{m}_{1}}=1\ 000\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] west
      [latex]\scriptsize {{m}_{2}}=1\ 500\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east
      [latex]\scriptsize {{v}_{{f1}}}={{v}_{{f2}}}={{v}_{f}}[/latex]
      Define west as positive.
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{v}_{f}}\cdot ({{m}_{1}}+{{m}_{2}})\\\therefore {{v}_{f}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}}}}{{({{m}_{1}}+{{m}_{2}})}}\\&=\displaystyle \frac{{1\ 000\ \text{kg}\times 20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+1\ 500\ \text{kg}\times (-25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{1\ 000\ \text{kg}+1\ 500\ \text{kg}}}\\&=-7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The velocity of the car and truck after the collision is [latex]\scriptsize \displaystyle 7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east.
   2. The learner is correct in that the magnitude of the force experienced by both vehicles will be the same while their direction will be opposite. This is Newton’s third law of motion which states that all forces between two objects exist in equal magnitude and opposite direction: if object A exerts a force [latex]\scriptsize {{F}_{\text{A}}}[/latex] on object B, then B simultaneously exerts a force [latex]\scriptsize {{F}_{\text{B}}}[/latex] on A, and the two forces are equal in magnitude and opposite in direction: [latex]\scriptsize {{F}_{\text{A}}}=-{{F}_{\text{B}}}[/latex].
   3. .
      [latex]\scriptsize \begin{align*}\text{Impulse} & =\Delta p\\&={{m}_{2}}{{v}_{{f2}}}-{{m}_{2}}{{v}_{{i2}}}\\&=1\ 500\ \text{kg}\times -\left( {7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-(-25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})} \right)\\&=27\ 000\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      Or [latex]\scriptsize 27\ 000\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] east
   4. .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{i}} & =E{{K}_{{i1}}}+E{{K}_{{i2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {1\ 000\ \text{kg}\times {{{\left( {20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+1\ 500\ \text{kg}\times {{{\left( {-25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=668\ 750\ \text{J}\end{align*}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{f}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{f1}}}^{2}+{{m}_{2}}\cdot {{v}_{{f2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {1\ 000\ \text{kg}\times {{{\left( {-7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+1\ 500\ \text{kg}\times {{{\left( {-7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=61\ 250\ \text{J}\end{align*}[/latex]
      Therefore [latex]\scriptsize E{{K}_{i}}\ne E{{K}_{f}}[/latex]. Kinetic energy was not conserved and so the collision was inelastic.
3. .
   1. Let the [latex]\scriptsize 3\ \text{kg}[/latex] object be object 1 and the [latex]\scriptsize 6\ \text{kg}[/latex] object be object 2.
      Define object 1’s initial direction as positive.
      [latex]\scriptsize {{m}_{1}}=3\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{{f1}}}=-2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{m}_{2}}=6\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\text{But}\ {{v}_{{i2}}}&=0\ m.{{s}^{{-1}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}}& ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{v}_{{f2}}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{1}}\cdot {{v}_{{f1}}}}}{{{{m}_{2}}}}\\&=\displaystyle \frac{{3\ \text{kg}\times 6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-3\ \text{kg}\times (-2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{6\ \text{kg}}}\\&=4\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The [latex]\scriptsize 6\ \text{kg}[/latex] object will move at [latex]\scriptsize \displaystyle 4\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the initial direction of the [latex]\scriptsize 3\ \text{kg}[/latex] object.
   2. .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{i}} & =E{{K}_{{i1}}}+E{{K}_{{i2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {3\ \text{kg}\times {{{\left( {6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+6\ \text{kg}\times {{{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=54\ \text{J}\end{align*}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{f}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{f1}}}^{2}+{{m}_{2}}\cdot {{v}_{{f2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {3\ \text{kg}\times {{{\left( {-2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+6\ \text{kg}\times {{{\left( {4\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=54\ \text{J}\end{align*}[/latex]
      .
      Therefore [latex]\scriptsize E{{K}_{i}}=E{{K}_{f}}[/latex]. Kinetic energy was conserved and so the collision was elastic.
4. .
   1. Let the locomotive be object 1 and the wagon be object 2.
      Define north as positive.
      [latex]\scriptsize {{m}_{1}}=4\ 500\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i1}}}=2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north
      [latex]\scriptsize {{m}_{2}}=7\ 000\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{{i2}}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{{f2}}}=1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north
      .
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\text{But}\ {{v}_{{i2}}}&=0\ m.{{s}^{{-1}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\therefore {{v}_{{f1}}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}-{{m}_{2}}\cdot {{v}_{{f2}}}}}{{{{m}_{1}}}}\\&=\displaystyle \frac{{4\ 500\ \text{kg}\times 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-7\ 000\ \text{kg}\times (1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{4\ 500\ \text{kg}}}\\&=0.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The locomotive will have a velocity of [latex]\scriptsize \displaystyle 0.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north after the collision.
   2. The conservation of momentum
   3. .
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{i}} & =E{{K}_{{i1}}}+E{{K}_{{i2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{i1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{i2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{i1}}}^{2}+{{m}_{2}}\cdot {{v}_{{i2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {4\ 500\ \text{kg}\times {{{\left( {2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+7\ 000\ \text{kg}\times {{{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=14\ 062.5\ \text{J}\end{align*}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}E{{K}_{f}} & =E{{K}_{{f1}}}+E{{K}_{{f2}}}\\&=\displaystyle \frac{1}{2}\cdot {{m}_{1}}\cdot {{v}_{{f1}}}^{2}+\displaystyle \frac{1}{2}\cdot {{m}_{2}}\cdot {{v}_{{f2}}}^{2}\\&=\displaystyle \frac{1}{2}\cdot \left( {{{m}_{1}}\cdot {{v}_{{f1}}}^{2}+{{m}_{2}}\cdot {{v}_{{f2}}}^{2}} \right)\\&=\displaystyle \frac{1}{2}\left( {4\ 500\ \text{kg}\times {{{\left( {0.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}+7\ 000\ \text{kg}\times {{{\left( {1.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}} \right)\\&=7\ 940.03\ \text{J}\end{align*}[/latex]
      .
      Therefore [latex]\scriptsize E{{K}_{i}}\ne E{{K}_{f}}[/latex]. Kinetic energy was not conserved and so the collision was inelastic.
   4. Now [latex]\scriptsize {{v}_{{f1}}}={{v}_{{f2}}}={{v}_{f}}[/latex].
      [latex]\scriptsize \displaystyle \begin{align*}{{m}_{1}}\cdot {{v}_{{i1}}}+{{m}_{2}}\cdot {{v}_{{i2}}} & ={{m}_{1}}\cdot {{v}_{{f1}}}+{{m}_{2}}\cdot {{v}_{{f2}}}\\\text{But}\ {{v}_{{i2}}} & =0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\\therefore {{m}_{1}}\cdot {{v}_{{i1}}} & ={{v}_{f}}\cdot ({{m}_{1}}+{{m}_{2}})\\\therefore {{v}_{f}} & =\displaystyle \frac{{{{m}_{1}}\cdot {{v}_{{i1}}}}}{{({{m}_{1}}+{{m}_{2}})}}\\&=\displaystyle \frac{{4\ 500\ \text{kg}\times 2.5\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{4\ 500\ \text{kg}+7\ 000\ \text{kg}}}\\&=0.98\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      The locomotive will have had a velocity of [latex]\scriptsize \displaystyle 0.98\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] north if the coupling had worked.

Back to Unit 2: Assessment