Unit outcomes

By the end of this unit you will be able to:

• Define electromagnetic (EM) radiation.
• Identify the EM spectrum and identify examples (light, radio waves, microwave, infrared, ultraviolet, x-rays and gamma rays).
• Describe the dual nature of EM radiation, i.e. wave and particle nature.
• Identify the relationship of wavelength to frequency to explain colour and energy of light.

What you should know

Before you start this unit, make sure you can:

• Explain how a wave is a periodic disturbance in a medium that transfers energy from one point to another. Refer to level 2 subject outcome 3.1 unit 1 if you need help with this.
• Explain the differences and similarities between transverse and longitudinal waves. Refer to level 2 subject outcome 3.1 unit 2 if you need help with this.
• Explain what is meant by wavelength, frequency, amplitude and period. Refer to level 2 subject outcome 3.1 unit 3 if you need help with this.
• Describe the electric field that exists around a point charge. Refer to level 3 subject outcome 4.1 unit 1 if you need help with this.
• Explain the principles of electromagnetism, especially how a moving charge produces a magnetic field and how a changing magnetic field produces or applies a force on a charged particle. Refer to level 3 subject outcome 4.2 units 1 and 2 if you need help with this.

Introduction

Sight is one of the most amazing senses we have. It allows us to interact with and experience the world in wonderful ways. Think of the beautiful sunsets you might have seen (see figure 1). So much of life is mediated through the gift of sight.

Figure 1: A beautiful sunset

But despite how amazing our sense of sight is, did you know that we can actually see very little of what there is to see with our eyes? Did you know that there are kinds of ‘light waves’ that you cannot see with your eyes? In fact, the light that we can see is just a small portion of a larger family of waves called the electromagnetic spectrum. We will see later on why it is called the electromagnetic spectrum.

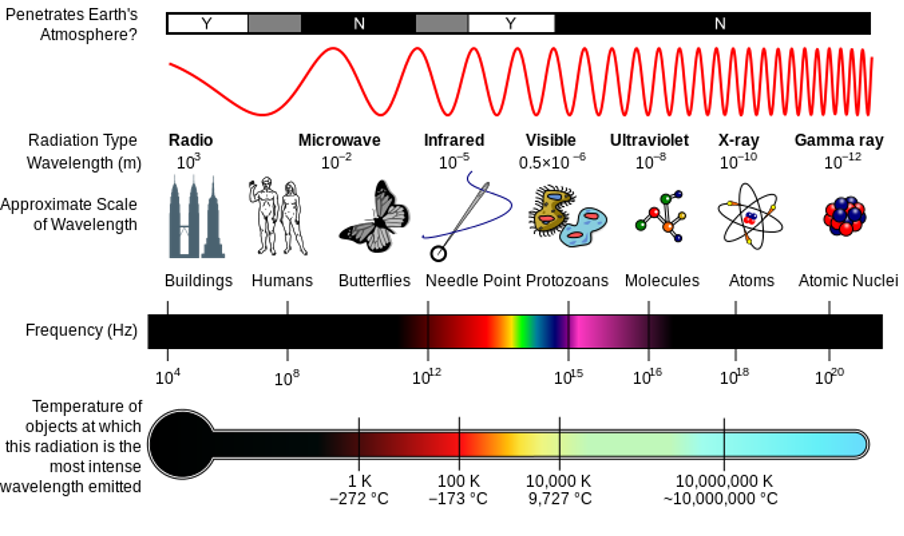
The electromagnetic spectrum

The so-called electromagnetic spectrum (the EM spectrum) consists of an extremely wide range of wave frequencies that transmit energy in the form of electromagnetic radiation. On the one end of the spectrum, we have radio waves which can have wavelengths of more than [latex]\scriptsize 1~000~\text{km}[/latex]. On the other end are gamma waves that can have wavelengths smaller than the nucleus of an atom. Figure 2 shows a summary of all the different types of waves that make up the EM spectrum.

As we move from left to right in figure 2, the wavelength of the waves gets shorter and shorter. This means that the frequency of the waves gets higher and higher. The higher the frequency of the wave, the more energy it can carry. This is why ultraviolet radiation, x-rays and gamma rays can be so dangerous. This radiation has enough energy to alter some chemical bonds in our cells which can lead to serious illness.

Figure 2: The electromagnetic spectrum

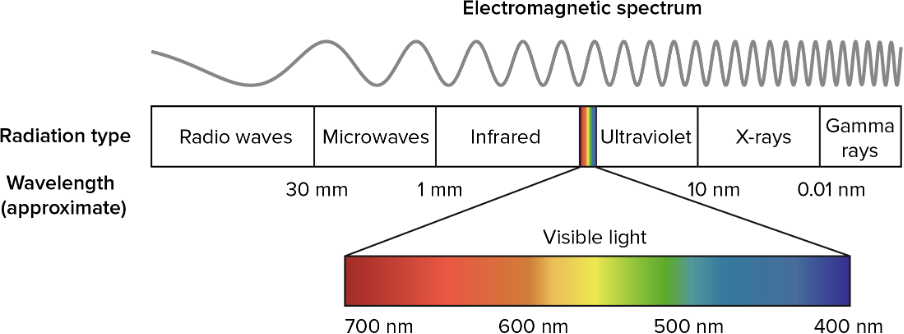
Somewhere in the middle of the EM spectrum is a little band of waves with wavelengths between about [latex]\scriptsize 700~\text{nm}[/latex] and [latex]\scriptsize 400~\text{nm}[/latex] called visible light that our eyes can see (see figure 3). By the way, a nanometre ([latex]\scriptsize \text{nm}[/latex]) is one billionth of a metre.

Figure 3: The visible light part of the EM spectrum

Figure 3 also shows us that red light has a longer wavelength (and hence lower frequency) than blue light. The higher frequency of blue light means that it carries more energy as well.

We will investigate each part of the EM spectrum and its applications in more detail in the next unit.

Properties of EM radiation

The waves in this spectrum have some important and unique properties. Firstly, you might remember in level 2 when we first talked about waves that we said that waves transfer energy through a medium and need a medium through which to travel. That is certainly true for water waves and sound waves, but it is not true for electromagnetic radiation waves. They do not need a medium and can propagate through empty space. They can, however, also travel through media such as air, water and you.

Secondly, we know that sound waves travel through the air at about [latex]\scriptsize 340~\text{m.s}^{-1}[/latex] (depending on the temperature). Next to EM waves, they are almost standing still. EM waves travel through a vacuum at about [latex]\scriptsize 300~000~000~\text{m.s}^{-1}[/latex]. That is almost [latex]\scriptsize 900~000[/latex] times faster! In fact, EM waves travel at the speed limit of the universe which we call the speed of light. We give this constant the symbol [latex]\scriptsize c[/latex]. The ‘[latex]\scriptsize c[/latex]’ in [latex]\scriptsize E=mc^2[/latex] is the speed of light. Just like other waves however, [latex]\scriptsize v = f \times \lambda[/latex] or for EM waves, [latex]\scriptsize c= f \times \lambda[/latex].

And lastly, EM waves are dual-natured. Depending on how we look at them they can behave like the ordinary transverse waves we have become familiar with, or they can behave like particles. We call the individual particles or packets of EM radiation photons.

Take note!

Important properties of electromagnetic radiation:

• EM radiation can propagate through a vacuum. It does not need a medium.
• EM radiation travels at the speed of light ([latex]\scriptsize c[/latex]) in a vacuum; [latex]\scriptsize c=299~792~458~\text{m.s}^{-1}[/latex].
• EM radiation obeys the wave equation [latex]\scriptsize v=f\times \lambda[/latex] or [latex]\scriptsize c=f\times \lambda[/latex].
• EM radiation has a dual nature. It can behave both as a transverse wave and as a particle.

Electromagnetic waves

You might think it strange to refer to light as an electromagnetic wave. What is electric or magnetic about light? This does not fit our everyday experience of light.

In level 3 subject outcome 4.1 unit 1, we drew the electric field that exists around a point charge. The charged particle creates an electric field that radiates out from the charge. Now, if we move this charged particle up and down, we will create a changing electric field in a particular region near the particle.

We know that a magnetic field is produced around a current-carrying wire. The reason is that there is a changing electric field around the wire. So, the changing electric field created by our oscillating charged particle will create a changing magnetic field.

Similarly, we know that a changing magnetic field results in a changing electric field. If there is a wire in the changing magnetic field, the electrons are made to move through the wire by the changing electric field. This is the basis of how generators work.

So, a changing electric field creates a changing magnetic field and a changing magnetic field creates an electric field. We have a positive feedback loop or chain reaction, and it is this mutual induction situation which propagates out as an electromagnetic wave due to the initial oscillation of our charged particle.

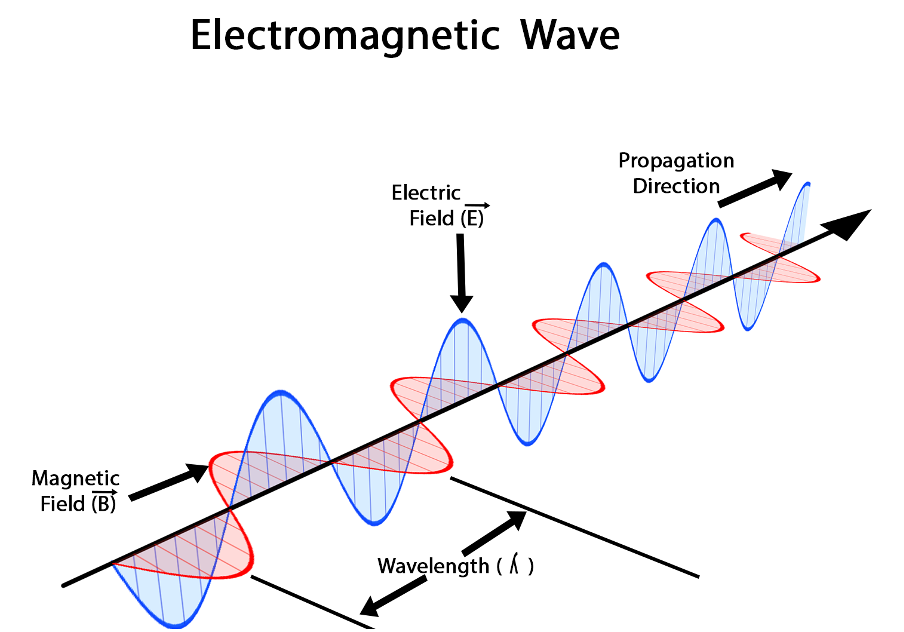
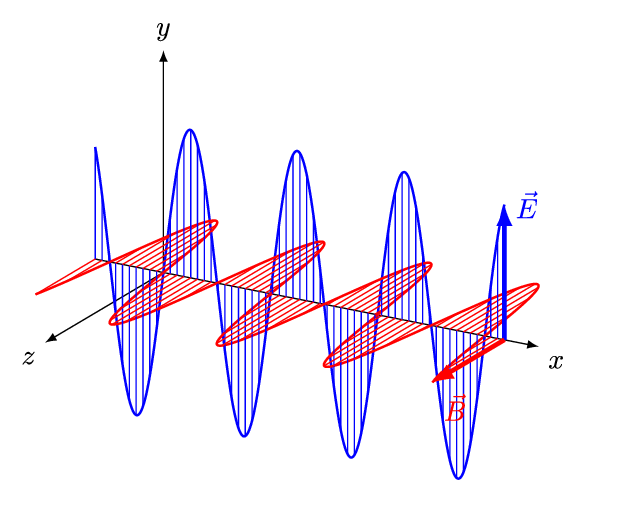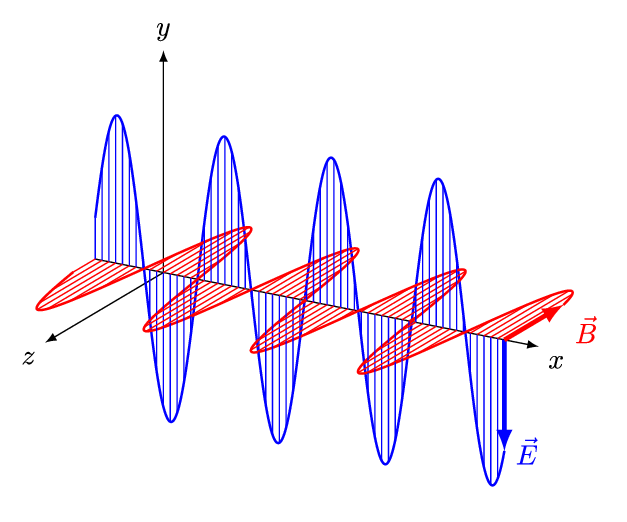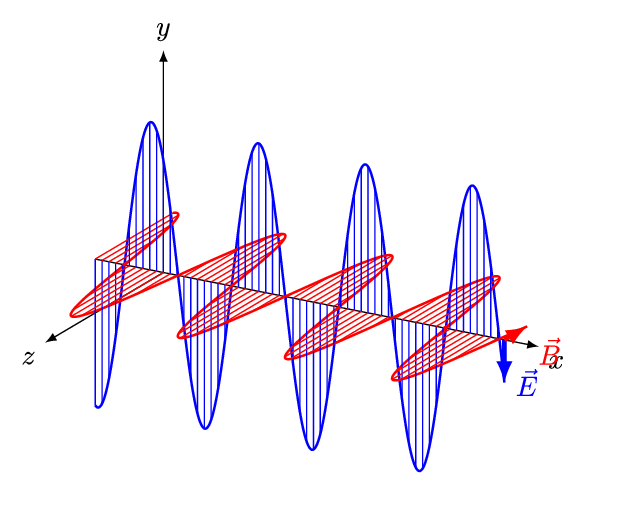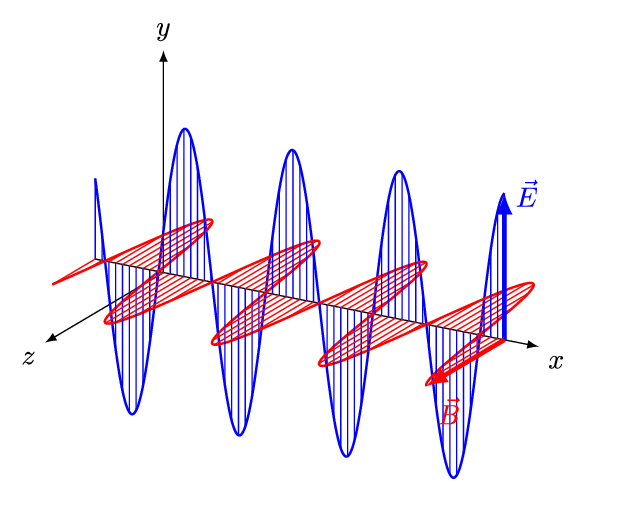
It is called an electromagnetic wave because it consists of an oscillating electric field and an oscillating magnetic field. These fields oscillate at right angles to each other and at right angles to the direction of the wave (see figure 4).

Figure 4: An electromagnetic wave

Figure 5 is an animation showing how an EM wave propagates.

Example 2.1

Calculate the frequency of an electromagnetic radio wave with a wavelength of [latex]\scriptsize 5.1~\text{m}[/latex].

Solution

EM waves obey the same wave equation that we have used before. The only difference is that we replace ‘[latex]\scriptsize v[/latex]’ in the equation with ‘[latex]\scriptsize c[/latex]’, the speed of light. Therefore, [latex]\scriptsize c=f\times \lambda[/latex] where [latex]\scriptsize c=300~000~000~\text{m.s}^{-1}[/latex].

We have been asked to calculate [latex]\scriptsize f[/latex]. All the given information is in SI units.
[latex]\scriptsize c=300~000~000~\text{m.s}^{-1}[/latex] (unless you are told otherwise, you can assume this value of [latex]\scriptsize c[/latex] for the speed of light in a vacuum)
[latex]\scriptsize \lambda=5.1~\text{m}[/latex]

[latex]\scriptsize \begin{align*} c&=f\times \lambda\\ \therefore f&=\displaystyle \frac{c}{\lambda}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{5.1~\text{m}}\\ &=58~823~529.41~\text{Hz} \end{align*}[/latex]

When we get very big answers like this, we usually convert the units or use scientific notation to simplify them. We can write the answer as [latex]\scriptsize 58.823~\text{MHz}[/latex] or [latex]\scriptsize 5.8823 \times 10^7~\text{Hz}[/latex].

Exercise 2.1

1. Red light has a wavelength of about [latex]\scriptsize 700~\text{nm}[/latex]. Calculate the frequency of red light.
2. An x-ray machine produces radiation with a frequency of [latex]\scriptsize 2.1 \times 10^{18}~\text{Hz}[/latex]. What is the wavelength of these waves?
3. A space telescope detects EM radiation with a frequency of [latex]\scriptsize 3.25 \times 10^{12}~\text{Hz}[/latex]. Can the human eye detect this radiation? Show a calculation to support your answer.

The full solutions are at the end of the unit.

Wave-particle duality

The section above explains how electromagnetic radiation behaves like a wave. It is the result of changing electric and magnetic fields that propagate out from a source like a wave. Light displays the same interference patterns associated with other kinds of waves. Wave-like properties like wavelength and frequency neatly explain the different energies associated with different parts of the EM spectrum as well as properties of light like colour.

But sometimes, light does not behave like a wave at all. Sometimes it behaves like a beam of particles. For example, if you shine light onto a metal surface, the light transfers some of its energy to the atoms in the metal but only in very specific and discrete amounts called quanta. In this case, it is as though light was a beam of little packets of energy. We call these packets of energy photons.

The energy of each photon is related to the wavelength of the EM radiation by a special number called Planck’s constant, named after Max Planck. Planck’s constant is given the symbol [latex]\scriptsize h[/latex] and [latex]\scriptsize h = 6.63 \times 10^{-34}~\text{J.Hz}^{-1}[/latex]. Sometimes you may see Planck’s constant written as [latex]\scriptsize h = 6.63 \times 10^{-34}~\text{J.s}[/latex]. Although this is technically correct [latex]\scriptsize \text{J.s}[/latex] are not the official SI units.

Take note!

The energy of a photon is calculated using [latex]\scriptsize E = hf[/latex] or [latex]\scriptsize E = h\cdot \displaystyle \frac{c}{\lambda}[/latex] where:

[latex]\scriptsize E[/latex] is the energy of the photon in [latex]\scriptsize \text{J}[/latex]
[latex]\scriptsize h = 6.63 \times 10^{-34}~\text{J.Hz}^{-1}[/latex] (Planck’s constant)
[latex]\scriptsize f[/latex] is the frequency of the wave in [latex]\scriptsize \text{Hz}[/latex]
[latex]\scriptsize c = 300~000~000~\text{m.s}^{-1}[/latex] (the speed of light in a vacuum)
[latex]\scriptsize \lambda[/latex] is the wavelength of the wave in [latex]\scriptsize \text{m}[/latex]

Example 2.2

Calculate the energy of a photon with a frequency of [latex]\scriptsize 5.6 \times 10^{17}~\text{Hz}[/latex].

Solution

We have been asked to calculate the energy of a photon and have been given the frequency. Therefore, we need to use the equation [latex]\scriptsize E = hf[/latex]. All the values have been given in standard units.

[latex]\scriptsize \begin{align*} E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 5.6\times10^{17}~\text{Hz}\\ &=3.7128\times 10^{-16}~\text{J} \end{align*}[/latex]

The energy of one photon is [latex]\scriptsize 3.7128\times 10^{-16}~\text{J}[/latex].

Example 2.3

Calculate the energy of one photon of infrared light with a wavelength of [latex]\scriptsize 0.021~\text{mm}[/latex].

Solution

We have been asked to calculate the energy of a photon and have been given the wavelength. Therefore, we need to use the equation [latex]\scriptsize E = h \cdot \displaystyle \frac{c}{\lambda}[/latex]. The wavelength is not in standard units and needs to be converted.

[latex]\scriptsize 0.021~\text{mm} = 2.1 \times 10^{-5}~\text{m}[/latex]

[latex]\scriptsize \begin{align*} E&=h\cdot \displaystyle \frac{c}{\lambda}\\ \therefore E&=6.63\cdot \displaystyle \frac{10^{-34}~\text{J.s}\times 300~000~000~\text{m.s}^{-1}}{2.1\times 10^{-5}~\text{m}}\\ &=9.47\times 10^{-21}~\text{J} \end{align*}[/latex]

The energy of one photon is [latex]\scriptsize 9.47\times 10^{-21}~\text{J}[/latex].

Exercise 2.2

1. Calculate the energy of a photon of EM radiation with a frequency of [latex]\scriptsize 4.67 \times 10^{12}~\text{Hz}[/latex].
2. Determine the energy of a photon of orange EM radiation with a wavelength of [latex]\scriptsize 630~\text{nm}[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• The electromagnetic spectrum (EM spectrum) consists of electromagnetic radiation waves with a very wide range of wavelengths (and therefore, frequencies).
• EM radiation can propagate through a vacuum. It does not need a medium.
• EM radiation travels at the speed of light ([latex]\scriptsize c[/latex]) in a vacuum; [latex]\scriptsize c = 299~792~458~\text{m.s}^{-1}[/latex].
• EM radiation obeys the wave equation [latex]\scriptsize v = f \times \lambda[/latex] or [latex]\scriptsize c= f \times \lambda[/latex].
• EM radiation has a dual nature. It can behave both as a transverse wave and as a particle.
• EM radiation consists of an electric field and a magnetic field oscillating at right angles to each other and to the direction of wave propagation.
• EM waves with a higher frequency are more energetic.
• The discrete packages of energy transmitted by EM radiation are called photons.
• The energy of a photon is calculated using [latex]\scriptsize E = hf[/latex] or [latex]\scriptsize E = h \cdot \displaystyle \frac{c}{\lambda}[/latex] where [latex]\scriptsize h[/latex] is Planck’s constant and [latex]\scriptsize h = 6.63 \times 10^{-34}~\text{J.s}[/latex].

Unit 2: Assessment

Suggested time to complete: 15 minutes

1. Calculate the wavelength of a radio wave with a frequency of [latex]\scriptsize 147.8~\text{kHz}[/latex]?
2. What is the energy of a photon of EM radiation with a frequency of [latex]\scriptsize 3.75 \times 10^{13}~\text{Hz}[/latex]?
3. What is the energy of a photon of light with a wavelength of [latex]\scriptsize 450~\text{nm}[/latex]?
4. What is the energy of a photon with a frequency of [latex]\scriptsize 12.56~\text{GHz}[/latex]?
5. Two photons are detected. One has a wavelength of [latex]\scriptsize 276~\text{nm}[/latex] and the other has a frequency of [latex]\scriptsize 400~\text{THz}[/latex]. Which has the longer wavelength?

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   [latex]\scriptsize \begin{align*} 700~\text{nm}&=700\times 10^{-9}~\text{m}\\ c&=f\times \lambda\\ \therefore f&=\displaystyle \frac{c}{\lambda}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{700\times 10^{-9}~\text{m}}\\ &=428~571.43\times 10^{9}~\text{Hz}\\ &=4.29\times 10^{14}~\text{Hz} \end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*} c&=f\times \lambda\\ \therefore \lambda&=\displaystyle \frac{c}{f}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{2.1\times 10^{18}~\text{Hz}}\\ &=142~857~142.486\times 10^{-18}~\text{m}\\ &=1.43\times 10^{-10}~\text{m} \end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*} \therefore \lambda &= \displaystyle \frac{c}{f}\\ &= \displaystyle \frac{300~000~000~\text{m.s}^{-1}}{3.25 \times 10^{12}~\text{Hz}}\\ &=9.23\times 10^{-5}~\text{m} \end{align*}[/latex]
   This wavelength falls outside of the visible spectrum of [latex]\scriptsize 700~\text{nm}[/latex] to [latex]\scriptsize 400~\text{nm}[/latex] and so cannot be detected by the human eye.

Back to Exercise 2.1

Exercise 2.2

1. .
   [latex]\scriptsize \begin{align*} E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 4.67\times 10^{12}~\text{Hz}\\ &=3.096\times 10^{-21}~\text{J} \end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*} 630~\text{nm}&=630\times 10^{-9}~\text{m}\\ E&=h\cdot \displaystyle \frac{c}{\lambda}\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\cdot \displaystyle \frac{300~000~000~\text{m.s}^{-1}}{630\times 1-^{-9}~\text{m}}\\ &=3.15\times 10^{-19}~\text{J} \end{align*}[/latex]

Back to Exercise 2.2

Unit 2: Assessment

1. .
   [latex]\scriptsize \begin{align*} 147.8~\text{kHz}&=1~478~000~\text{Hz}\\ c&=f\times \lambda\\ \therefore \lambda&=\displaystyle \frac{c}{f}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{1~478~000~\text{Hz}}\\ &=202.98~\text{m} \end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*} E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 3.75\times 10^{13}~\text{Hz}\\ &=2.48\times 10^{-20}~\text{J} \end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*} 450~\text{nm}&=450\times10^{-9}~\text{m}\\ E&=h\cdot \displaystyle \frac{c}{\lambda}\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\cdot \displaystyle \frac{300~000~000~\text{m.s}^{-1}}{450\times 10^{-9}~\text{m}}\\ &=4.41\times 10^{-19}~\text{J} \end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*} 12.56~\text{GHz}&=12.56\times10^{9}~\text{Hz}\\ E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 12.56\times 10^{9}~\text{Hz}\\ &=8.32\times 10^{-24}~\text{J} \end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*} 400~\text{THz}&=400\times10^{12}~\text{Hz}\\ c&=f\times \lambda\\ \therefore \lambda&=\displaystyle \frac{c}{f}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{400\times 10^{12}~\text{Hz}}\\ &=750\times 10^{-9}~\text{m}\\ &=750~\text{nm} \end{align*}[/latex]
   The photon with a frequency of [latex]\scriptsize 400~\text{THz}[/latex] has a longer wavelength.

Back to Unit 2: Assessment