Waves, sound and light: Describe and apply properties of waves in everyday life contexts
Unit 3: Applications of electromagnetic radiation
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Identify the applications of radiation across the EM spectrum.
- Define lasers and give examples of their application.
- Explain and apply the photoelectric effect and give examples of its application.
What you should know
Before you start this unit, make sure you can:
- Explain what EM radiation is.
- Use the wave equation to calculate either the wavelength or frequency of EM radiation.
- Calculate the energy of a photon of EM radiation given either the wavelength or frequency.
Refer to unit 2 if you need help with any of this.
Introduction
In the previous unit we learnt what electromagnetic radiation is, how it forms and what properties it has. We noted that EM radiation covers an extremely wide range of wavelengths and frequencies and that we have classified different segments of the EM spectrum into different kinds of waves.
In this unit, we are going to explore the applications of these different kinds of EM radiation, but it is important to remember that a radio wave with a wavelength of a few hundred metres is fundamentally the same thing as visible light with a wavelength of [latex]\scriptsize 500~\text{nm}[/latex] or a gamma ray with a wavelength of a few picometres. They are all EM radiation. They all obey the same laws. They are all formed in much the same way, and they propagate in the same way. All that is different is that they have different wavelengths and hence different frequencies and energies.
Applications of the EM spectrum
This section is based on College Physics. Authored by: OpenStax College. License: CC BY.[1]
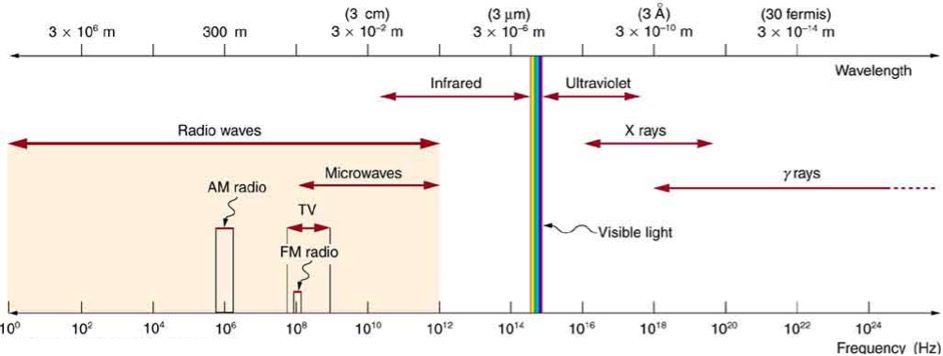
Figure 1 shows the full electromagnetic spectrum and which portions of it are used for specific applications. We can see, for example, that the part of the spectrum typically used for TV broadcasting also contains a small section for FM radio and that AM radio uses radiation with a far longer wavelength (about [latex]\scriptsize 100[/latex] times longer).
Figure 1: The EM spectrum
Figure 1 also shows us that the different segments of the spectrum tend to overlap. There are no hard and firm rules about what is an X-ray and what is a gamma ray. It is all electromagnetic radiation with an almost infinite range of wavelengths. We only segment the spectrum like this so that we have some idea of the kind of wavelengths, frequencies and energies that are involved.
Table 1 lists the general segments of the EM spectrum and how waves in the range of each segment tend to be produced and what applications the EM radiation generally has. Gamma radiation, we can see, is generally produced when the unstable nuclei atoms lose energy by radiation. Hence another word for this is radioactive decay.
| Type of EM radiation | Production | Applications | Life sciences aspect | Issues |
| Radio and TV | Accelerating charges | Communications, remote controls | MRI | Requires controls for band use |
| Microwaves | Accelerating charges and thermal agitation | Communications, ovens, radar | Deep heating | Cell phone use |
| Infrared | Thermal agitations and electronic transitions | Thermal imaging, heating | Absorbed by the atmosphere | Greenhouse effect |
| Visible light | Thermal agitations and electronic transitions | All pervasive | Photosynthesis, human vision | |
| Ultraviolet | Thermal agitations and electronic transitions | Sterilisation, cancer control | Vitamin D production | Ozone depletion, cancer causing |
| X-rays | Inner electronic transitions and fast collisions | Medical, security | Medical diagnosis, cancer therapy | Cancer causing |
| Gamma rays | Nuclear decay | Nuclear medicine, security | Medical diagnosis, cancer therapy | Cancer causing, radiation damage |
Let’s take a closer look at each broad type of EM radiation and their applications.
Radio waves
Radio waves are the longest wavelength, lowest frequency and lowest energy EM radiation. They are produced on Earth by passing alternating currents through wires and other conductors. This part of the spectrum gets its name because of the major applications of radiation in this range – that of transmitting information, first by radio transmitters and receivers and later by television systems.
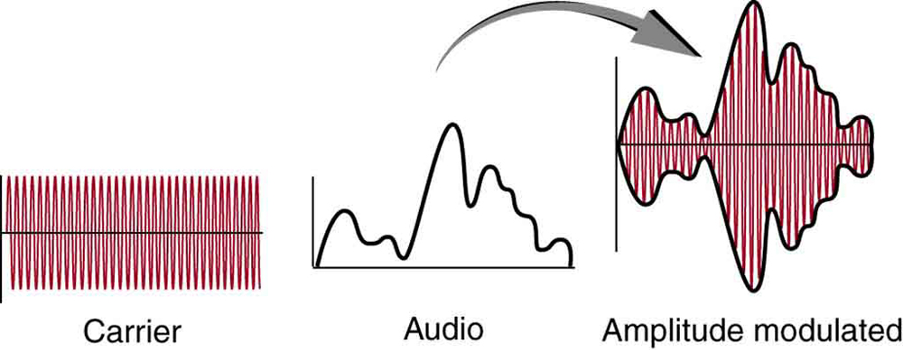
AM radio stations use frequencies between [latex]\scriptsize 540~\text{kHz}[/latex] and [latex]\scriptsize 1~600~\text{kHz}[/latex]. AM stands for amplitude modulation. A wave of a specific and constant frequency (the carrier wave) has its amplitude modified or modulated by an audio signal (see figure 2). The receiver is tuned to have a resonant frequency matching the carrier wave and uses the changes in amplitude to replicate the original audio.
Figure 2: Amplitude modulation
FM radio uses a slightly different technique. FM stands for frequency modulation. Instead of the carrier wave’s amplitude being changed or modulated to carry the information, its frequency is changed (see figure 3).
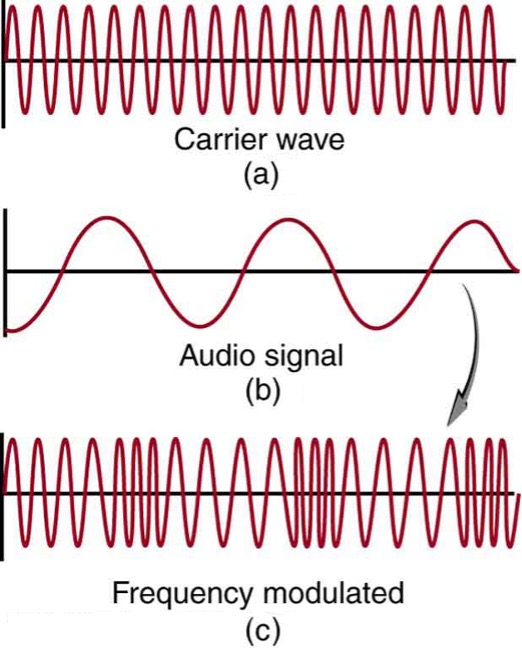
FM uses frequencies between [latex]\scriptsize 88~\text{MHz}[/latex] and [latex]\scriptsize 108~\text{MHz}[/latex]. Because the frequency of the wave needs to be able to be changed by the range of human hearing (about [latex]\scriptsize 20~\text{kHz}[/latex]) FM radio stations cannot be closer together on the dial than [latex]\scriptsize 20~\text{kHz}[/latex] or [latex]\scriptsize 0.02~\text{MHz}[/latex]. Interference (destructive and constructive) from other sources of EM radiation can more easily change a wave’s amplitude than its frequency, therefore, FM radio suffers less from ‘noise’ than does AM radio. However, the lower frequencies used for AM mean that the longer wavelength waves are able to get around objects such as buildings and hills meaning that they tend to be better when broadcasting over longer ranges.
Traditional terrestrial television broadcasts typically use AM for the visuals and FM for the audio. TV uses the [latex]\scriptsize 54~\text{MHz}[/latex] and [latex]\scriptsize 88~\text{MHz}[/latex] and [latex]\scriptsize 174~\text{MHz}[/latex] and [latex]\scriptsize 222~\text{MHz}[/latex] bands. Satellite television and newer digital terrestrial broadcast use higher frequencies still (up to [latex]\scriptsize 1~000~\text{MHz}[/latex] or more depending on regulations).
Mobile phone networks use frequencies in the range of [latex]\scriptsize 1.9~\text{GHz}[/latex] and magnetic resonance imaging (MRI) typically operates in the [latex]\scriptsize 100~\text{MHz}[/latex] range. It is a general rule of thumb that the higher the frequency of the radio wave, the more information it can carry.
Extremely low frequency (ELF) radio waves of about [latex]\scriptsize 1~\text{kHz}[/latex] are used to communicate with submarines because these waves are able to penetrate salt water quite well.
Many pieces of modern technology produce radio waves as a by-product. Perhaps the most pervasive are those produced by electricity transmission grids running at [latex]\scriptsize 50~\text{Hz}[/latex] or [latex]\scriptsize 60~\text{Hz}[/latex]. These have extremely long wavelengths of about [latex]\scriptsize 6~000~\text{km}[/latex] but due to their low energy do not penetrate buildings and other structures well.
Figure 4: Transmission grids produce long wavelength EM radiation at [latex]\scriptsize 50~\text{Hz}[/latex] or [latex]\scriptsize 60~\text{Hz}[/latex]
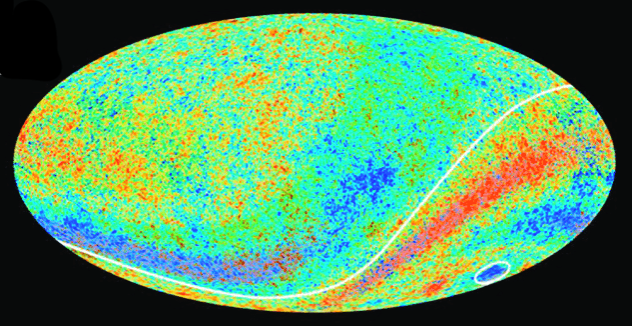
Radio waves are not only created on Earth by people. Certain astronomical phenomena also generate waves in the same range and these waves carry important information about these phenomena and the universe more generally. For example, the cosmic microwave background radiation has given astronomers one of the best pictures of how the universe probably formed and subsequently expanded (see figure 5).
But all the radio waves created on Earth can interfere with these astronomical efforts. This is why regulations control what wavelengths can be produced and where no EM radiation can be created at all. The two sites of the Square Kilometre Array (a huge radio telescope project) are being built in the middle of unpopulated deserts in Australia and South Africa (see figure 6) so that they are as far from any man-made EM radiation as possible.
Figure 6: The Square Kilometre Array (SKA) site, north of Carnarvon, Northern Cape, South Africa
Microwaves
Microwaves are the highest frequency EM radiation that can be produced, like radio waves, by electric currents in macroscopic circuits. They are so named because, next to radio waves, they have very small wavelengths. Typical frequencies range from [latex]\scriptsize 10^{9}~\text{Hz}[/latex] to [latex]\scriptsize 10^{12}~\text{Hz}[/latex].
The most known application of microwave radiation is the microwave oven for heating and cooking food. The energy in the EM radiation ([latex]\scriptsize 2.45~\text{GHz}[/latex]) is ultimately transferred to the water molecules in the food which gets hot and cooks.
Activity 3.1: What are the holes for?
Time required: 10 minutes
What you need:
- a microwave oven
- a ruler
What to do:
- Assuming that the microwave radiation generated by the oven is [latex]\scriptsize 2.45~\text{GHz}[/latex], calculate the wavelength of the microwaves produced (in [latex]\scriptsize \text{mm}[/latex]).
- Look at the door of the microwave. Measure the diameter of the holes in the metal grid.
- How do the holes in the grid compare to the wavelength you calculated? With this in mind, what do you think this grid is for?
What did you find?
- .
[latex]\scriptsize \begin{align*} 2.45~\text{GHz}&=2.45\times10^{9}~\text{Hz}\\ c&=f\times \lambda\\ \therefore \lambda&=\displaystyle \frac{c}{f}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{2.54\times 10^{9}~\text{Hz}}\\ &=0.122~\text{m}\\ &=122~\text{mm} \end{align*}[/latex] - The diameter of the holes in the grid should be about [latex]\scriptsize 1~\text{mm}[/latex].
- The holes are much smaller than the wavelength of the microwaves. Therefore, the grid effectively stops all the microwaves from escaping from the oven, reflecting them back inside the oven but the holes still allow you to see how your food is doing.
Cooking food is not all that microwaves are good for. Microwaves are also the basis of radar. Radar is a detection system that uses the reflection and doppler shift of EM radiation in the microwave range to determine the distance, angle, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. Special radar systems are used to map the Earth and other planets. The smaller the wavelength used, the greater the detail that can be produced.
We noted above that the higher the frequency of the EM radiation, the more information it can carry. This is exploited in microwave-based communications, like satellite systems and internet backbones. But higher frequencies mean lower wavelengths and so microwave communications require ‘line of sight’. The receiver must be able to ‘see’ the transmitter without having any obstacles in the way.
Figure 7: A microwave communications tower
Infrared radiation
Infrared means ‘below red’ and includes those frequencies just below visible light and the upper end of the microwave range (although there is some overlap). When we think of infrared, we tend to think of night-vision scopes. These devices can detect the infrared radiation that is emitted by warm and hot objects.
Infrared radiation is produced by thermal motion – the vibration and rotation of atoms and molecules. The hotter something is, the more the atoms and molecules within it vibrate, the more infrared radiation it emits. The Sun, being really hot, emits a huge amount of infrared radiation. About half of the EM radiation received from the Sun is in the form of infrared radiation.
Half of this is absorbed by the Earth and then radiated back into space. Water molecules ([latex]\scriptsize \text{H}_2\text{O}[/latex]) and carbon dioxide ([latex]\scriptsize \text{CO}_2[/latex]) molecules are especially good at absorbing and re-emitting infrared radiation. Therefore, most of the radiation emitted from the Earth is absorbed by [latex]\scriptsize \text{CO}_2[/latex] and [latex]\scriptsize \text{H}_2\text{O}[/latex] in the atmosphere and then radiated back to Earth or into outer space. This radiation back to Earth is known as the greenhouse effect but is generally a good thing. Without it, the surface temperature of the Earth would be about [latex]\scriptsize 40^{\circ}\text{C}[/latex] lower. However, the more [latex]\scriptsize \text{CO}_2[/latex] and [latex]\scriptsize \text{H}_2\text{O}[/latex] is in the atmosphere, the more radiation is absorbed and re-emitted back to Earth which seems to be resulting in higher global temperatures.
Visible light
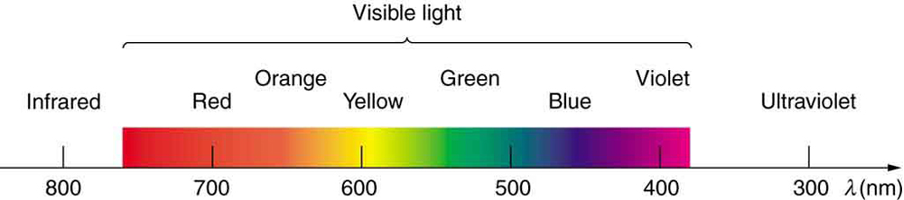
About [latex]\scriptsize 44%[/latex] of the EM radiation from the Sun is in the visible light range of [latex]\scriptsize 750~\text{nm}[/latex] and [latex]\scriptsize 400~\text{nm}[/latex]. Given the full spectrum that spans about [latex]\scriptsize 20[/latex] orders of magnitude, this is a very narrow band indeed. As figure 8 shows, we perceive light with the lowest frequency as red and light with the highest frequencies as violet. When the full spectrum is viewed together, we perceive white.
Figure 8: The visible light part of the EM spectrum
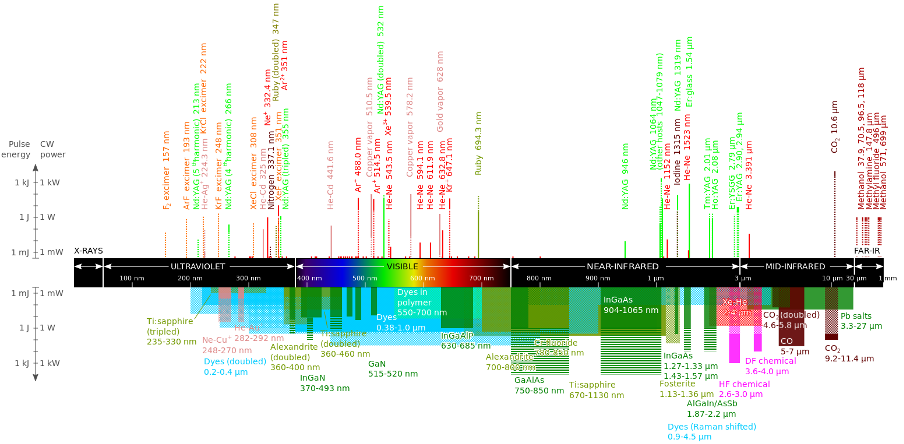
A common application of EM radiation in this part of the spectrum is Light Amplification by Stimulated Emission of Radiation (LASER). Not all lasers produce EM radiation in the visible spectrum, but many do (see figure 9).
Figure 9 Types of lasers with their operating wavelengths
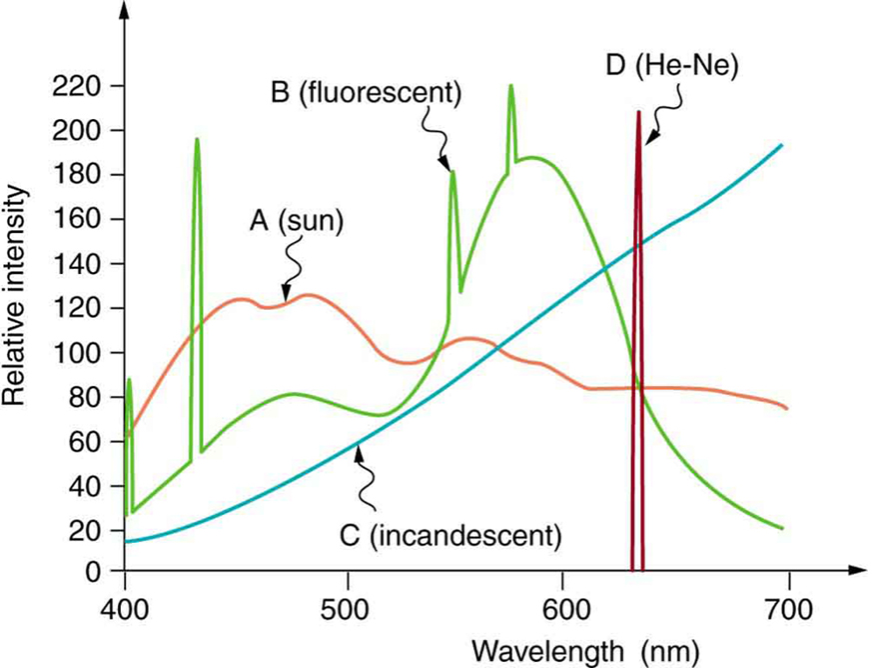
Lasers are unique in that they produce EM radiation that is coherent. That means that the light produced is in a very narrow range of frequencies and intensities. Figure 10 shows the difference between several light sources. We can see that the light from a helium-neon laser (D) has a very narrow band of frequencies in it.
Figure 10: The very narrow spectrum of frequencies in a red light helium-neon laser (D) compared to other light sources
Lasers can be found everywhere – from CD players and pointers to, satellite communication systems, eye correction surgery, industrial cutting and distance detection.
Note
To find out more about how laser light is created, watch the video called How a Laser Works.
Ultraviolet light
Ultraviolet (UV) means ‘above violet’ and extends from the highest frequency of visible light. The ultraviolet spectrum includes waves from about [latex]\scriptsize 400~\text{nm}[/latex] to [latex]\scriptsize 10~\text{nm}[/latex] in wavelength. Some of the Sun’s radiation is in the UV spectrum and is split into three categories:
- UV-A ([latex]\scriptsize 320-400\text{nm}[/latex]) – lowest energy
- UV-B ([latex]\scriptsize 290-320\text{nm}[/latex])
- UV-C ([latex]\scriptsize 220-290\text{nm}[/latex]) – highest energy.
Almost all UV-B and UV-C is absorbed by the ozone layer. Repeated and extensive exposure to any UV radiation can lead to skin cancer and other conditions such as cataracts. Exposure to UV radiation suffered by blast furnace workers in England in the late 1800s led many to become blind and the invention of the very first pair of sunglasses.
Staying in the shade, wearing protective clothing and wearing sunscreen are all effective ways of preventing over-exposure to UV radiation. However, some exposure is beneficial. UV-B, for example, stimulates the production of vitamin D, important for the prevention of some kinds of cancers and in general mood regulation.
UV radiation is typically used to sterilise objects and surfaces. In many clinics in South Africa, UV lamps are used to kill airborne pathogens especially those causing Tuberculosis (TB).

X-rays
While the low-frequency end of the X-ray range overlaps with the ultraviolet, X-rays extend to much higher frequencies (and energies). They are created by very high voltage discharges into rarefied low pressure gasses. They were called X-rays because the scientists who discovered them did not know what they were.
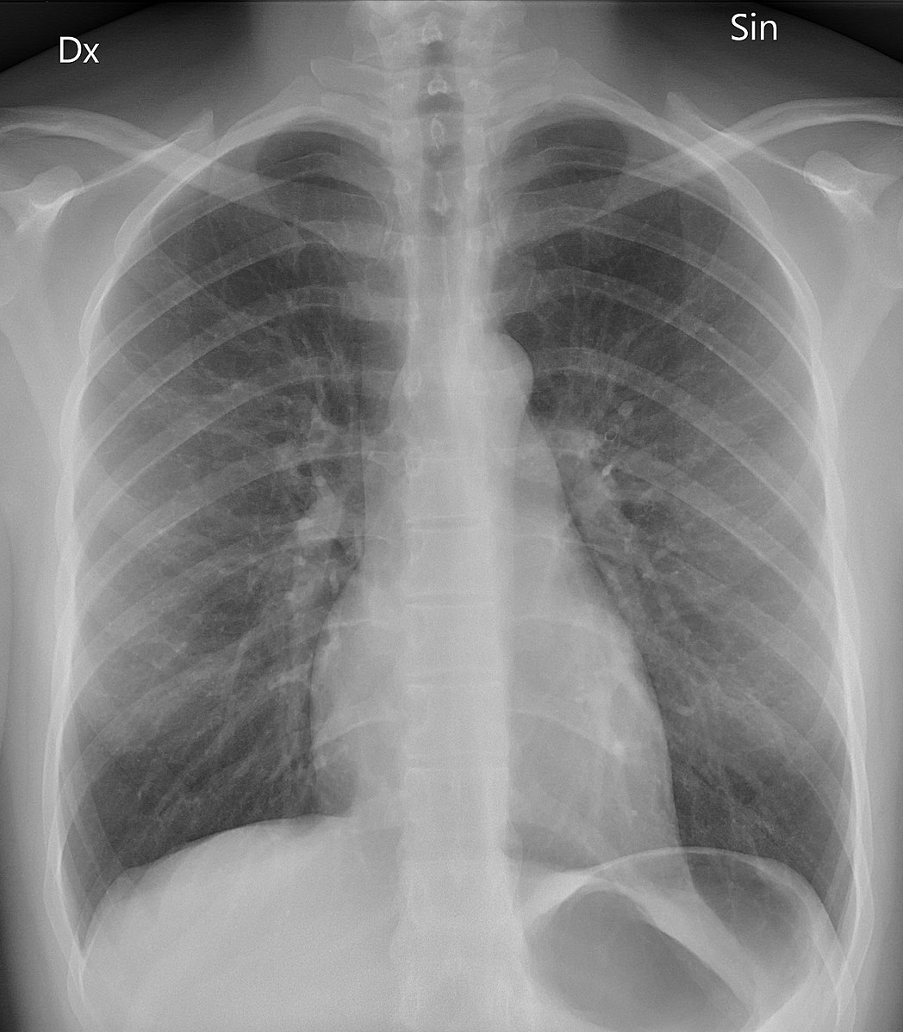
Like UV radiation, X-rays have enough energy to damage living organisms. However, because they have higher energies, X-rays can penetrate deeper into the body than UV radiation. But used under controlled and targeted conditions, this same energy and penetration power can be used to kill cancer cells and ‘see’ inside the body. X-rays pass more easily through the soft tissues of the body than cartilage and bone. This difference is then processed to produce the X-ray image we are all familiar with (see figure 12).
Figure 12: A typical X-ray image
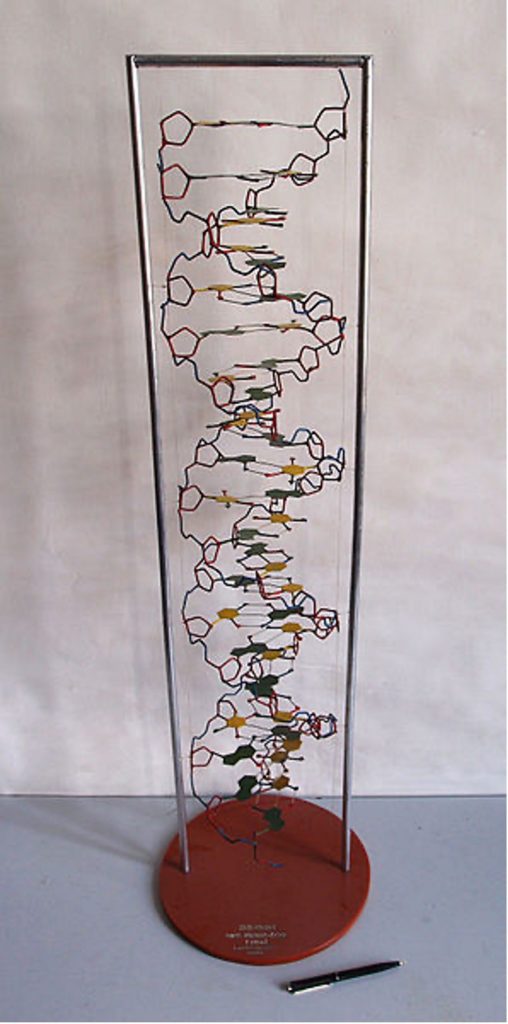
X-rays have wavelengths less than [latex]\scriptsize 0.01~\text{nm}[/latex]. Therefore, they can also be used to detect the shapes of molecules based on how the radiation diffracts off the molecule. This kind of X-ray diffraction was most famously used by Francis Crick and James Watson in determining the shape of the DNA double-helix (see figure 13).
Figure 13: A DNA model made by Crick and Watson
Gamma rays
Gamma rays are classified as any EM radiation emitted by a nucleus. They have extremely high frequencies and short wavelengths. Gamma rays are therefore even more penetrating and damaging to living organisms but can also be used in very controlled and targeted ways such as cancer therapies or for internal imaging. These kinds of applications fall under nuclear medicine.
Gamma rays occur naturally through a process of radioactive decay of certain materials in rocks and the soil and through many processes in space. Whether produced on Earth or in space, gamma rays are constantly bombarding our bodies.
Take note!
Three rules that apply to electromagnetic waves in general are as follows:
- High-frequency EM waves are more energetic and are able to penetrate more than low-frequency waves.
- High-frequency EM waves can carry more information per unit time than low-frequency waves.
- The shorter the wavelength of any EM wave probing a material, the smaller the detail it is possible to resolve.
Note that there are exceptions to these rules of thumb.
The photoelectric effect
We learnt about the dual nature of light in the previous unit. Sometimes it behaves like a wave and sometimes it behaves like a stream of particles. For a long time, scientists thought that EM radiation was purely a continuous transverse wave (continuous flow of energy). It seemed to do all the things that other transverse waves do. This certainly helped to explain phenomena such as diffraction and interference.
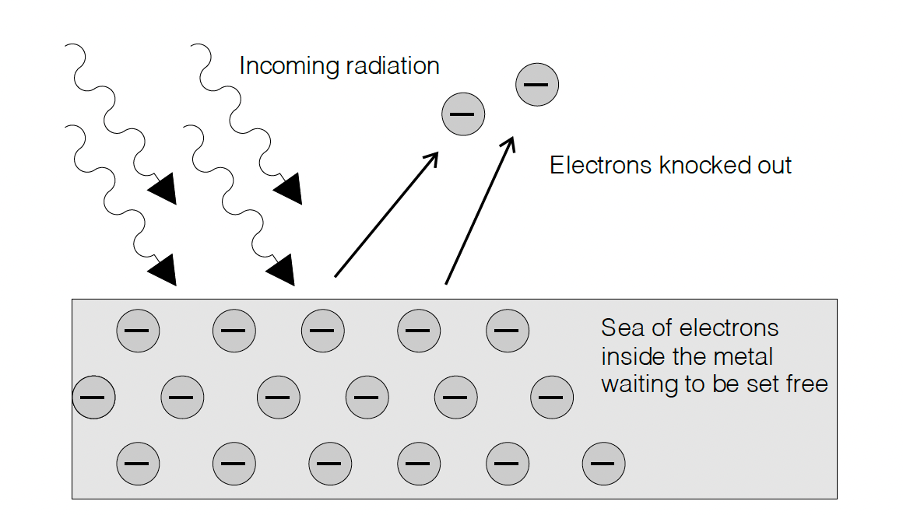
However, in 1887 Heinrich Hertz (a German physicist and, yes, THAT Hertz) noticed that ultraviolet light, when shone on a metal plate, could cause sparks. The energy in the light gave the electrons in the metal enough energy to escape and the result was visible sparks.
The initial expectation was that, given enough time, EM radiation of any frequency would eventually cause sparks on any metal and that more sparks would result from a brighter light of the same frequency. It was thought that if the frequency or the intensity was initially too low, the electrons would gradually absorb more and more light energy until they were able to escape and cause sparks. However, experimental results showed this not to be the case.
Over time, it was noticed that different metals required light of different frequencies for the same effect. Then in 1902, Philipp Lenard (a Hungarian physicist) discovered that the maximum velocity with which electrons are ejected by ultraviolet light is entirely independent of the intensity of the light. How could this be? Surely the brighter the light, the more energy the electrons would be able to absorb and the greater their escape velocity would be.
A deep paradox existed at the heart of physics that no one could explain. That is until Albert Einstein took a break from his work on relativity. He proposed that people were thinking about the problem all wrong. He said that the EM radiation was not behaving like a continuous transverse wave but rather like a stream of tiny packets of energy called quanta (now called photons). All the photons in light of a particular frequency had exactly the same amount of energy and it did not matter if there were only a few photons (dim light) or lots of photons (bright light).
He said that a photon gave up all its discrete energy to an electron in the metal and this is what allowed these electrons to escape and cause sparks (see figure 14).
Figure 14: The photoelectric effect
For many years, scientists were very sceptical of these ideas even though they explained the observed results very well. They were sceptical because Einstein solved the central paradox by introducing another one – that EM radiation can behave as a wave or as a particle, it just depends on how you look at it!
It turned out that Einstein was right and that his was the correct explanation of the photoelectric effect. It explained why:
- electrons are emitted immediately when EM radiation is shone on a metal,
- the intensity of EM radiation makes no difference to the maximum kinetic energy of the emitted electrons, and
- the photoelectric effect is only observed with different metals at different minimum frequencies.
Take note!
The photoelectric effect is the process whereby an electron is emitted by a substance when electromagnetic radiation shines on it.
- Electrons are emitted immediately when EM radiation is shone on a metal.
- The intensity of EM radiation makes no difference to the maximum kinetic energy of the emitted electrons.
- Different metals required different minimum frequencies for the photoelectric effect to be observed.
Note
If you have an internet connection, you should watch an excellent demonstration of the photoelectric effect called Photoelectric Effect Demonstration.
The photoelectric equation
The energy needed to eject an electron from a substance is called that substance’s work function ([latex]\scriptsize W_0[/latex]), and this is basically the amount of work that needs to be done to get an electron to escape. If the energy of a photon is less than the work function, then there is no emission and no sparks. It does not matter how many photons land on the metal, as one electron can only absorb one photon. Table 2 lists the [latex]\scriptsize W_0[/latex] values for a few common substances.
| Element | Work Function([latex]\scriptsize \text{eV}[/latex]) |
| Aluminium | 4.08 |
| Beryllium | 5.0 |
| Cadmium | 4.07 |
| Calcium | 2.9 |
| Carbon | 4.81 |
| Cesium | 2.1 |
| Cobalt | 5.0 |
| Copper | 4.7 |
| Gold | 5.1 |
| Iron | 4.5 |
| Lead | 4.14 |
| Magnesium | 3.68 |
| Mercury | 4.5 |
| Nickel | 5.01 |
| Niobium | 4.3 |
| Potassium | 2.3, 2.29 |
| Platinum | 6.35 |
| Selenium | 5.11 |
| Silver | 4.26-4.73 |
| Sodium | 2.28, 2.36 |
| Uranium | 3.6 |
| Zinc | 4.3 |
Note that the units in the table are given as electron volts ([latex]\scriptsize \text{eV}[/latex]) where [latex]\scriptsize 1~\text{eV} = 1.6 \times 10^{-19}~\text{J}[/latex].
Remember, each photon has a discrete and fixed amount of energy depending on the radiation’s frequency. These two quantities are related by Planck’s constant in the equation [latex]\scriptsize E = hf[/latex] or ([latex]\scriptsize E = h\cdot \displaystyle \frac{c}{\lambda}[/latex]).
This is why there is a minimum frequency of EM radiation required for different substances with different work functions. We call this minimum frequency the cut-off (or threshold) frequency ([latex]\scriptsize f_0[/latex]). Therefore, we can say that [latex]\scriptsize W_0 = hf_0[/latex].
Take note!
The work function ([latex]\scriptsize W_0[/latex]) is the minimum energy needed to knock an electron out of a metal. As it is energy, it measured in joules ([latex]\scriptsize \text{J}[/latex]).
The cut-off frequency ([latex]\scriptsize f_0[/latex]) is the minimum frequency of EM radiation needed to achieve the work function for a particular substance.
Now, we also know that energy is conserved. Any energy in a photon in addition to that required to achieve the work function goes into the electrons escape velocity or kinetic energy ([latex]\scriptsize E_K[/latex]). This excess photon energy is actually the maximum kinetic energy ([latex]\scriptsize E_{Kmax}[/latex]) of an electron emitted right on the surface of the substance. Electrons further down need additional energy to reach the surface before being ejected and so there is not the full excess amount available as kinetic energy.
We can therefore represent the total energy of a photon ([latex]\scriptsize E[/latex]) that emits an electron for a given substance as:
[latex]\scriptsize E = W_0+E_{K max}[/latex] or [latex]\scriptsize E_{K max} = hf-W_0[/latex] (remember that [latex]\scriptsize E = hf[/latex])
This is the photoelectric equation.
Take note!
The photoelectric equation is:
[latex]\scriptsize E = W_0 + E_{K max}[/latex]
Or
[latex]\scriptsize E_{K max} = hf-W_0[/latex]
Note
If you have an internet connection watch the video called Photoelectric effect for an excellent summary of all we have discussed.
Example 3.1
UV light ([latex]\scriptsize \lambda = 245~\text{nm}[/latex]) is shone on a sodium surface ([latex]\scriptsize W_0 = 4.41 \times 10^{−19}~\text{J}[/latex]). What is the maximum kinetic energy an emitted electron can have?
Solution
We need to calculate the maximum kinetic energy i.e [latex]\scriptsize E_{K max}[/latex].
[latex]\scriptsize E_{K max} = hf-W_0[/latex] but we have been given the wavelength not the frequency. Therefore, we can change the equation to [latex]\scriptsize E_{K max} = h\cdot \displaystyle \frac{c}{\lambda}-W_0[/latex].
[latex]\scriptsize \begin{align*} W_0&=6.9\times 10^{-19}~\text{J}\\ \lambda&=245~\text{nm}=245\times 10^{-9}~\text{m}\\ h&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\\ c&=300~000~000~\text{m.s}^{-1}\\ E_{K max}&=h\cdot \displaystyle \frac{c}{\lambda}-W_0\\ \therefore E_{K max}&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\cdot \displaystyle \frac{300~000~000~\text{m.s}^{-1}}{245\times 10^{-9}~\text{m}}-6.9\times 10^{-19}~\text{J}\\ &=1.22\times 10^{-19}~\text{J} \end{align*}[/latex]
Therefore, the maximum kinetic energy that any emitted electron can have will be [latex]\scriptsize 1.22 x 10^{-19}~\text{J}[/latex].
Example 3.2
UV light ([latex]\scriptsize f = 4.6 x 10^{15}~\text{Hz}[/latex]) is incident to a sodium surface ([latex]\scriptsize W_0 = 4.41 \times 10^{−19}~\text{J}[/latex]). Would any surface electrons be emitted?
Solution
We need to determine if the energy in a photon is greater than the work function.
[latex]\scriptsize \begin{align*} f&=4.6\times 10^{15}~\text{Hz}\\ h&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\\ E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 4.6\times 10^{15}~\text{Hz}\\ &=3.05\times 10^{-18}~\text{J} \end{align*}[/latex]
Therefore, electrons will be emitted as the energy of each photon is greater than the work function of sodium.
Exercise 3.1
Question 1 adapted from Everything Science Grade 12 Worked Example 3: Photoelectric effect
- A metal surface is illuminated with ultraviolet light of wavelength [latex]\scriptsize 330~\text{nm}[/latex]. Electrons are emitted from the metal surface. The minimum amount of energy required to emit an electron from the surface of this metal is [latex]\scriptsize 3.5 x 10^{-19}~\text{J}[/latex].
- Name the phenomenon illustrated above.
- What is the term for ‘the minimum amount of energy required to emit an electron from the surface’?
- Calculate the frequency of the ultraviolet light.
- Calculate the kinetic energy of a photoelectron emitted from the surface of the metal when the ultraviolet light shines on it.
- The intensity of the ultraviolet light illuminating the metal is now increased. What effect will this change have on the kinetic energy of the emitted photoelectrons? (Write down only INCREASES, DECREASES or REMAINS THE SAME.)
- The intensity of the ultraviolet light illuminating the metal is now increased. What effect will this change have on the number of photoelectrons emitted per second? (Write down only INCREASES, DECREASES or REMAINS THE SAME.)
- A light of an unknown wavelength is incident to silver foil. The light has only enough energy to eject electrons from the silver foil but not enough to give them kinetic energy.
- If the same light is incident on copper foil, would electrons be ejected? ([latex]\scriptsize W_0 = 7.5 x 10^{-19}~\text{J}[/latex])
- If the same light is incident on silicon, would electrons be ejected? ([latex]\scriptsize W_0 = 1.8 x 10^{-19}~\text{J}[/latex])
- If the intensity of the light on the silver foil is increased, what happens?
- If the frequency of the light incident on the silver foil is increased, what happens?
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- Every part of the EM spectrum has practical applications.
- Laser stands for Light Amplification by Stimulated Emission of Radiation.
- Laser light is unique in that it is coherent – all the light is in phase and of a very similar wavelength and frequency.
- The photoelectric effect was key to helping scientists understand the dual nature of EM radiation – that it can behave like a continuous transverse wave and like a stream of particles called photons.
- The photoelectric effect occurs when the energy in photons of EM radiation is sufficient to knock electrons out of a substance.
- The work function ([latex]\scriptsize W_0[/latex]) is the minimum amount of energy required for a substance to emit an electron.
- The cut-off frequency or threshold frequency ([latex]\scriptsize f_0[/latex]) is the minimum frequency of EM radiation required for the photoelectric effect to occur.
- The photoelectric equation is [latex]\scriptsize E = W_0 + E_{K max}[/latex] or [latex]\scriptsize E_{K max} = hf-W_0[/latex].
Unit 3: Assessment
Suggested time to complete: 25 minutes
Question 1 adapted from NC(V) Physical Sciences Paper 1 November 2019 question 11
- Ultraviolet light with a frequency of [latex]\scriptsize 3 x 10^{15}~\text{Hz}[/latex] strikes a metal surface and ejects photoelectrons that have a maximum kinetic energy of [latex]\scriptsize 9.76 x10^{-19}~\text{J}[/latex].
- Calculate the minimum amount of energy required to emit an electron from the metal.
- Calculate the threshold frequency of the metal.
- What effect will an increase in frequency have on the: (only write INCREASES, DECREASES or NO EFFECT)
- speed of the photoelectrons?
- number of photoelectrons released?
- Explain how the intensity of the incident light affects the number of photoelectrons ejected from the metal surface.
Question 2 adapted from NC(V) Physical Sciences Paper 1 February 2019 question 11
- Ultraviolet light with a wavelength of [latex]\scriptsize 280~\text{nm}[/latex] is shone on a metal surface. Electrons are emitted from the metal surface. The minimum amount of energy required to emit electrons from the surface of the metal is [latex]\scriptsize 3.5 x 10^{-19}~\text{J}[/latex].
- What is the NAME given to the minimum amount of energy required to emit electrons from the surface of the metal?
- Calculate the frequency of the ultraviolet light.
- Calculate the kinetic energy of the electrons emitted from the surface of the metal.
- The intensity of the ultraviolet light illuminating the metal is decreased. What effect will this have on the following: (write down only INCREASES/ DECREASES/REMAINS THE SAME)
- the kinetic energy of the emitted electrons?
- the number of electrons emitted per second?
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- .
- This is the photoelectric effect.
- The work function.
- .
[latex]\scriptsize \begin{align*} \lambda&=330~\text{nm}=330\times 10^{-19}~\text{m}\\ c&=300~000~000~\text{m.s}^{-1}\\ c&=f\times \lambda\\ \therefore f&=\displaystyle \frac{c}{\lambda}\\ &=\displaystyle \frac{300~000~000~\text{m.s}^{-1}}{330\times 10^{-19}~\text{m}}\\ &=9.09\times 10^{20}~\text{Hz} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} W_0&=3.5\times 10^{-19}~\text{J}\\ f&=9.09\times 10^{20}~\text{Hz}\\ h&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\\ E_{K max}&=hf-W_0\\ &=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 9.09\times 10^{20}~\text{Hz}-3.5\times 10^{-19}~\text{J}\\ &=6.03\times 10^{14}~\text{J} \end{align*}[/latex] - REMAINS THE SAME
- INCREASES
- .
- No. The work function of copper is greater than silver. Therefore, the photons would need to have more energy to eject electrons from copper.
- Yes. The work function of silicon is less than silver. Therefore, the photons would have enough energy to eject electrons from silicon.
- More electrons per second are emitted but they have the same maximum kinetic energy.
- The same number of electrons would be emitted per second but each of these would have greater maximum kinetic energy.
Unit 3: Assessment
- .
- .
[latex]\scriptsize \begin{align*} f&=3\times 10^{15}~\text{Hz}\\ h&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\\ E&=hf\\ \therefore E&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\times 3\times 10^{15}~\text{Hz}\\ &=1.989\times 10^{-18}~\text{J} \end{align*}[/latex]
.
[latex]\scriptsize \begin{align*} E_{K max}&=9.76\times 10^{-19}~\text{J}\\ E&=W_0+E_{K max}\\ \therefore W_0&=E-E_{K max}\\ &=1.989\times 10^{-18}~\text{J}-9.76\times 10^{-19}~\text{J}\\ &=10.13\times 10^{-19}~\text{J} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} E&=10.13\times 10^{-19}~\text{J}\\ h&=6.63\times 10^{-34}~\text{J.Hz}^{-1}\\ E&=hf\\ \therefore f&=\displaystyle \frac{E}{h}\\ &=\displaystyle \frac{10.13\times 10^{-19}~\text{J}}{6.63\times 10^{-34}~\text{J.Hz}^{-1}}\\ &=1.53\times 10^{15}~\text{Hz} \end{align*}[/latex] - .
- Increase
- No effect
- The greater the intensity, the more photons hit the material per second. The more photons that hit the material, the more electrons will be emitted by the material.
- .
- .
- Work function
- .
[latex]\scriptsize \begin{align*} \lambda&=280~\text{nm}=280\times 10^{-9}~\text{m}\\ c&=3\times 10^{8}~\text{m.s}^{-1}\\ c&=f\times \lambda\\ \therefore f&=\displaystyle \frac{c}{\lambda}\\ &=\displaystyle \frac{3\times 10^{8}~\text{m.s}^{-1}}{280\times 10^{-9}~\text{m}}\\ &=1.07\times 10^{15}~\text{Hz} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} h&=6.63\times 10^{-34}~\text{J}\\ W_0&=3.5\times 10^{-19}~\text{J}\\ f&=1.07\times 10^{15}~\text{Hz}\\ E_{K max}&=hf-W_0\\ &=6.63\times 10^{-34}~\text{J}\times 1.07\times 10^{15}~\text{Hz}-3.5\times 10^{-19}~\text{J}\\ &=3.59\times 10^{-19}~\text{J} \end{align*}[/latex] - .
- Remains the same
- Decreases
Media Attributions
- figure1 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure2 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure3 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure4 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure5 © ESA-Planck collaboration is licensed under a CC BY (Attribution) license
- figure6 © Mike Peel is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Bidgee is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Lumen Learning is licensed under a CC BY (Attribution) license
- figure9 © Danh is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure10 © OpenStax is licensed under a CC BY (Attribution) license
- figure11 © FaciliesNet is licensed under a CC0 (Creative Commons Zero) license
- figure12 © Mikael Häggström is licensed under a CC0 (Creative Commons Zero) license
- figure13 © David Ludwig is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure14 © Siyavula is licensed under a CC BY-SA (Attribution ShareAlike) license
- Located at: http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics. ↵
- Source: https://courses.lumenlearning.com/physics/chapter/24-3-the-electromagnetic-spectrum/ - CC-BY 4.0 ↵
- Special Permission Obtained - https://www.dropbox.com/s/wqxhxg68zmaw1y8/STEM%20Learning%20copyright_%20permission%20Photoelectric%20Effect%20Demonstration.pdf?dl=0 ↵