Unit 1: The Doppler effect

Dylan Busa

Waves, sound and light: Describe and apply properties of waves in everyday life contexts

Unit 1: The Doppler effect

Dylan Busa

By the end of this unit you will be able to:

Identify and describe the basic concepts of the Doppler effect with sound and ultrasound.
Apply the Doppler effect to radar and examples of sonic boom.

What you should know

Before you start this unit, make sure you can:

Describe how the frequency of a sound wave affects the pitch of the sound. See level 3 subject outcome 3.1 unit 2 if you need help with this.

Introduction

Even if you don’t realise it, you have more than likely heard of the Doppler effect in action. Examples of it are the way ambulance and police car sirens change in as they approach you or get further away.

Click here to listen to the Doppler effect.

Doppler effect (Duration: 00.03)

Because of your experience, you instinctively know that the hooter’s pitch going up indicates that the car is approaching and as the hooter’s pitch decreases, the car is travelling away again. The Doppler effect does not only apply to sound waves though. It applies to all waves including light waves and other forms of electromagnetic radiation. To understand why, we need to take a closer look at what is happening.

The Doppler effect is named after the Austrian physicist Christian Doppler (see figure 1), who described the phenomenon in 1842. Doppler was a mathematician and physicist.

https://en.wikipedia.org/wiki/File:Christian_Doppler.jpg - PD — Figure 1: Christian Doppler

The Doppler effect

You may have noticed that the Doppler effect only happens when something is moving. Most of our everyday experiences of the Doppler effect occur when a vehicle, the source of the sound, is moving relative to us, the observer (or listener in the case of sound waves). In this case, the source is moving, and the observer is stationary.

Let’s explore this simple case of the source moving relative to a stationary observer. As the source of the sound, a car’s hooter for example, moves towards us, it is travelling in the same direction as the sound waves it emits that will reach our ears (see figure 2). But because it is moving towards us, the waves in front of the source get bunched up. This means that more waves pass a given point each second which means that there is an increase in the frequency. Because there is an increase in frequency, we hear a higher pitched sound.

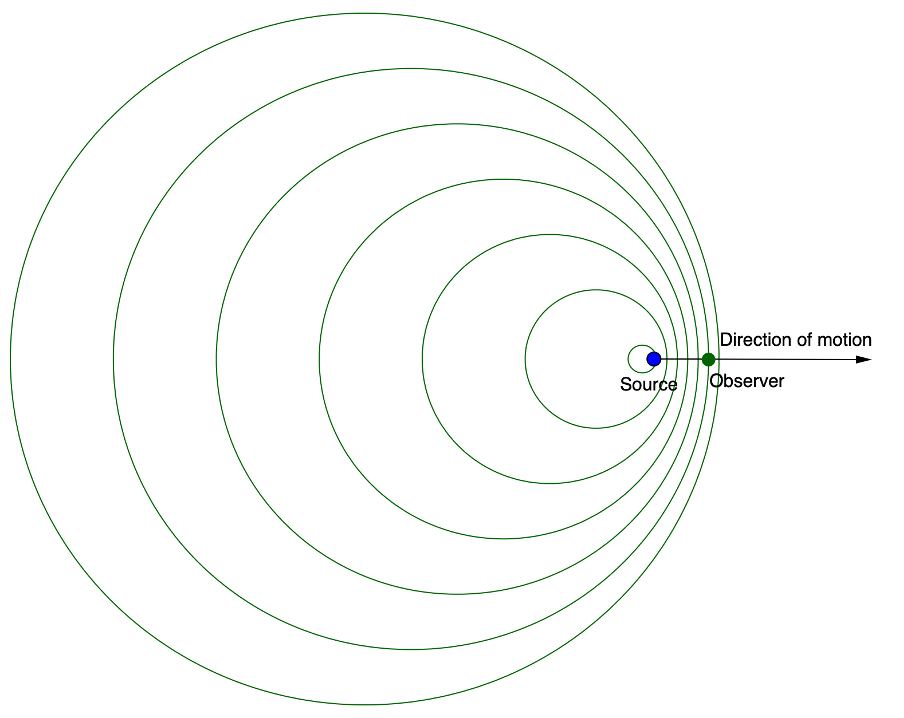
Figure 2: The Doppler effect when a source is travelling towards an observer

It is important to note that the frequency of the sound wave from the source does not change. It is our perception of this frequency that has changed.

When a source moves away from us, the reverse happens. The waves behind the source get more spread out, resulting in a lower frequency and hence a lower perceived pitch (see figure 3).

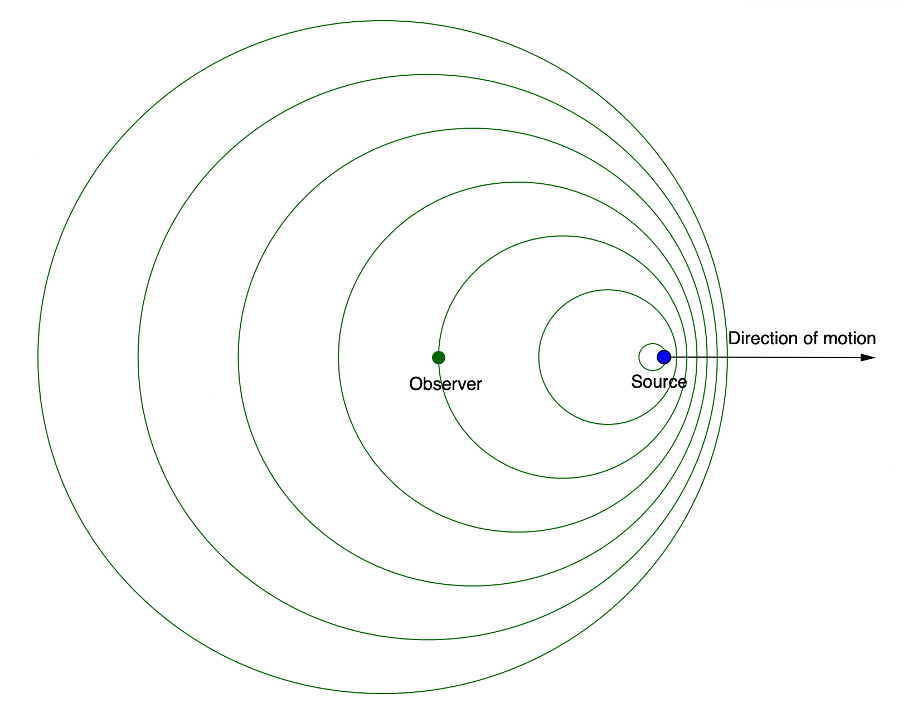
Figure 3: The Doppler effect when a source is travelling away from an observer

However, it need not be the source that is moving. An observer who is moving relative to a stationary source will also experience the Doppler effect. An observer moving towards a source will experience the waves at a higher frequency and so will hear a higher pitched sound. An observer moving away from a source will experience the waves at a lower frequency and so will hear a lower pitched sound.

In fact, both the source and the observer can be moving. What is important is that there is relative motion between the source and the observer.

The Doppler effect is the apparent change in the frequency of a wave caused by the relative motion between the wave’s source and the observer.

Time required: 10 minutes

What you need:

a mobile phone or other small, light source of sound
string (three to four metres long)

What to do:

Tie a three to four metre piece of string around your mobile phone (or some other small and light sound source). Make sure that the string is tied tightly and across all four sides like a bow around a present.
Go outside into a large, open space and play a song or some other sound on the mobile phone.
Ask a friend to stand nearby while you swing the phone carefully above your head making sure that you don’t let it crash into anything or anyone.
Ask your friend to describe how the sound changes as the phone comes towards them and then moves away again.
Swop roles so that you can hear the sound effect of the phone moving towards and away from you.
Does changing the speed of the phone affect how much the sound changes?

What did you find?

As the phone moved through the air you should have heard a change in the pitch of the sound coming from the phone. As the phone moved towards you, the pitch of the sound goes up. As the phone moves away from you, the pitch of the sound goes down.

This is because, as the phone moves towards you, the sound waves in front of the phone get bunched up and so more waves pass a certain point in a given time. There is a perceived change in the frequency of the sound and so the pitch of the sound increases.

The exact opposite happens as the phone moves away from you.

You should also have found that the extent of the change in the pitch of the sound coming from the phone (both the increase and decrease in pitch) was greater the faster the phone was moving. The faster the phone moves, the more bunched up or spread out the sound waves become and so the greater the extent in the perceived change in frequency and pitch.

If you have an internet connection, watch the video called What is the Doppler Effect? for an excellent explanation and demonstration of the Doppler effect.

What is the Doppler Effect? (Duration: 02.30)

You should also play around with the interactive Doppler effect simulation at this link.

Change the velocity of the source ( $\scriptsize v_S$ ) to see how this affects the extent of the Doppler effect experienced by the Observer (R). Notice that the frequency of the waves emitted by the source never changes. What changes is the perceived frequency of the waves by the observer. Each time a wave front hits the observer, it blinks.

Calculate the Doppler effect

If we know the speed of the waves, the frequency of the waves and the relative speeds of the source and observer, we can calculate the frequency that the observer will perceive using the following formula.

$\scriptsize f_L=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S$

Where:
$\scriptsize f_L$ is the frequency perceived by the observer (or listener)
$\scriptsize f_S$ is the frequency of the source
$\scriptsize v$ is the speed of the wave through the medium
$\scriptsize v_L$ is the speed of the listener
$\scriptsize v_S$ is the speed of the source

Remember that $\scriptsize v_L$ and $\scriptsize v_S$ are vectors. The signs of these quantities will tell us if the relative motion of the source and observer (or listener) is towards or away from each other.

If the source is moving towards the observer, $\scriptsize v_S$ is negative.
If the observer is moving towards the source, $\scriptsize v_L$ is positive.

A police car with a siren sounding at $\scriptsize 750~\text{Hz}$ is driving along a road at $\scriptsize 22~\text{m.s}^{-1}$ . You are standing on the pavement. If the speed of sound in air is $\scriptsize 344~\text{m.s}^{-1}$ ., what frequency will you hear as:

the car travels towards you?
the car travels away from you?

Solutions

All the values given are in SI units so we do not need to do any conversions before we can calculate. We have been asked in each case for the frequency perceived by the listener.

$\scriptsize \begin{align*} f_S&=750~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{listener is stationary}\\ v_S&=-22~\text{m.s}^{-1}&&\text{source is moving towards listener}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left ( \displaystyle \frac{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}-22~\text{m.s}^{-1}} \right )\cdot 750~\text{Hz}\\ \therefore f_L&=801.24~\text{Hz} \end{align*}$
This answer makes sense as we expect the observer to perceive the siren at a higher pitch (i.e. a higher frequency) as the car comes towards them.
$\scriptsize \begin{align*} f_S&=750~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{listener is stationary}\\ v_S&=22~\text{m.s}^{-1}&&\text{source is moving away from the listener}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left ( \displaystyle \frac{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}+22~\text{m.s}^{-1}} \right )\cdot 750~\text{Hz}\\ \therefore f_L&=704.92~\text{Hz} \end{align*}$
This answer makes sense as we expect the observer to perceive the siren at a lower pitch (i.e. a lower frequency) as the car moves away from them.

A fire truck is driving towards a building in which a fire alarm is ringing at $\scriptsize 825~\text{Hz}$ . The truck is travelling at $\scriptsize 18~\text{m.s}^{-1}$ . If the speed of sound in air is $\scriptsize 344~\text{m.s}^{-1}$ , what frequency do the firemen in the truck hear?

Solution

All the values given are in SI units so we do not need to do any conversions before we can calculate. We have been asked for the frequency perceived by the listener.

$\scriptsize \begin{align*} f_S&=825~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=18~\text{m.s}^{-1}&&\text{listener is moving towards the source}\\ v_S&=0~\text{m.s}^{-1}&&\text{source is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left ( \displaystyle \frac{344~\text{m.s}^{-1}+18~\text{m.s}^{-1}}{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}} \right )\cdot 825~\text{Hz}\\ \therefore f_L&=868.17~\text{Hz} \end{align*}$

This answer makes sense as we expect the observer to perceive the siren at a higher pitch (i.e. a higher frequency) as they move towards the source.

A hearing-impaired passenger is at a train station. They can only hear frequencies above $\scriptsize 900~\text{Hz}$ . The train approaches the platform at a constant speed of $\scriptsize 85~\text{km/h}$ and sounds its whistle as a warning. The whistle sounds at $\scriptsize 815~\text{Hz}$ . Assume the speed of sound in air is $\scriptsize 344~\text{m.s}^{-1}$ .

Will the person hear the warning whistle? Explain your answer.
What frequency would the whistle need to be for the person to hear it if the train travelled at the same speed of $\scriptsize 85~\text{km/h}$ ?
At what speed would the train need to travel for the person to hear the whistle if the frequency is $\scriptsize 800~\text{Hz}$ ?

Solution

Not all the values given are in SI units. We need to convert the speed of the train to $\scriptsize \text{m.s}^{-1}$ .
$\scriptsize 85~\text{km/h}=23.61~\text{m.s}^{-1}$ .

We have been asked for the frequency perceived by the listener.
$\scriptsize \begin{align*} f_S&=815~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{listener is stationary}\\ v_S&=-23.61~\text{m.s}^{-1}&&\text{source is moving towards listener}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left ( \displaystyle \frac{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}-23.61~\text{m.s}^{-1}} \right )\cdot 815~\text{Hz}\\ \therefore f_L&=875.06~\text{Hz} \end{align*}$
The frequency of the sound of the train whistle perceived by the observer is $\scriptsize 875.06~\text{Hz}$ . This means that the person will not be able to hear the sound as it is below their audible threshold.
We have been asked to calculate the frequency of the whistle such that the frequency perceived by the listener would be $\scriptsize 900~\text{Hz}$ .
$\scriptsize \begin{align*} f_L&=900~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{listener is stationary}\\ v_S&=-23.61~\text{m.s}^{-1}&&\text{source is moving towards listener}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_S&=\displaystyle \frac{f_L}{\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )}\\ \therefore f_S&=\displaystyle \frac{900}{\left(\displaystyle \frac{344~\text{m.s}^{-1}\pm 0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}-23.61~\text{m.s}^{-1}} \right )}\\ \therefore f_S&=838.23~\text{Hz} \end{align*}$
The frequency of the sound of the train whistle would need to be at least $\scriptsize 838.23~\text{Hz}$ to be heard by the listener.
We have been asked to calculate the speed that the train must travel at such that the frequency perceived by the listener would be $\scriptsize 900~\text{Hz}$ of a whistle with a frequency of $\scriptsize 815~\text{Hz}$ .
$\scriptsize \begin{align*} f_L&=900~\text{Hz}\\ f_S&=815~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{listener is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore \displaystyle \frac{f_S}{f_L}&=\displaystyle \frac{v\pm v_S}{v\pm v_L}\\ \therefore \displaystyle \frac{f_S}{f_L}\cdot (v\pm v_L)&=v\pm v_S\\ \therefore v_S&=\displaystyle \frac{f_S}{f_L}\cdot (v\pm v_L)-v\\ \therefore v_S&=\displaystyle \frac{815~\text{Hz}}{900~\text{Hz}}\times (344~\text{m.s}^{-1}+0~\text{m.s}^{-1})-344~\text{m.s}^{-1}\\ &=-32.49~\text{m.s}^{-1} \end{align*}$
The speed of the approaching train would need to be at least $\scriptsize 32.49~\text{m.s}^{-1}$ towards the listener for the train whistle to be heard by the listener.

You will only ever need to answer questions where either the source or the observer are moving, never both.

Passengers in a car hear its hooter at a frequency of $\scriptsize 812~\text{Hz}$ . What frequency does someone standing on the pavement hear as the car moves directly towards them at a speed of $\scriptsize 85~\text{km/h}$ ? Assume the speed of sound in air is $\scriptsize 340~\text{m.s}^{-1}$ .

Question 2 adapted from Everything Science Grade 12 Exercise 6-1 question 3

A small plane is taxiing directly away from you down a runway. The noise of the engine, as the pilot hears it, has a frequency $\scriptsize 1.15$ times the frequency that you hear. What is the speed of the plane? Assume the speed of sound in air is $\scriptsize 340~\text{m.s}^{-1}$ .
An experiment was done in the South Pole. The temperature was $\scriptsize -40^{\circ}\text{C}$ . A source, moving away from an observer at $\scriptsize 22.5~\text{m.s}^{-1}$ , emitted a sound at $\scriptsize 2~500~\text{Hz}$ . The observer measured a frequency of only $\scriptsize 2~335~\text{Hz}$ . What was the speed of sound at this cold temperature?

Question 4 adapted from Everything Science Grade 12 Exercise 6-1 question 5

Cecil approaches a source emitting a sound with a frequency of 437.1 Hz. Assume the speed of sound is 344 m.s−1.
1. How fast does Cecil need to move to observe a frequency that is $\scriptsize 20$ percent higher?
2. If he passes the source at this speed, what frequency will he measure when he is moving away?

The full solutions are at the end of the unit.

Applications of the Doppler effect

As we said above, the Doppler effect applies to all waves. Light from a source travelling towards you will be perceived to have a slightly higher frequency and will shift blue (blueshift). Light from a source travelling away from you will be perceived to have a slightly lower frequency and will shift red (redshift). This is illustrated in figure 4.

Figure 4: Redshift and blueshiftThis effect is used to determine whether distant galaxies are travelling towards or away from us. The extent of the blueshift or redshift can be used to determine how fast another galaxy is approaching or receding.

Traffic cops use exactly the same technique to measure the speed of motorists using radio waves. This is called radar.

The radar gun (see figure 5) fires a burst of radio waves towards an approaching vehicle. If the vehicle was stationary, these radio waves would be reflected back at exactly the same frequency. However, if the car is moving towards the gun, the waves get reflected back at a slightly higher frequency. The gun compares the frequency of the reflected waves with the source waves and uses the difference to calculate the speed of the vehicle. The faster the vehicle is travelling, the greater the change in frequency.

The same principle underpins all radar applications including those used to track the path of aircraft as well as storms.

Figure 5: A radar speed gun

Sonic booms

The phenomena of sonic booms can be thought of as the Doppler effect on steroids. Have a look at the formula we have been using to calculate the frequency of the sound perceived by the observer.

$\scriptsize f_L=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S$

What happens as $\scriptsize v_S$ gets closer and closer to $\scriptsize v$ ? Can you see that the denominator gets very, very small meaning that the whole fraction gets very, very big. This means that $\scriptsize f_L$ gets very big and approaches infinity as $\scriptsize v_S$ approaches $\scriptsize v$ .

When this happens, a sonic boom occurs. A sonic boom is the sound associated with the shock waves created by an object travelling through the air, at or faster than, the speed of sound. They create a large amount of energy, and sound like explosions. The ‘crack’ of a bullwhip is a result of a sonic boom.

If you have an internet connection, watch and listen how a Meteor creates sonic boom burning up in the atmosphere.

Meteor creates sonic boom burning up in the atmosphere (Duration: 00.45)

As the speed of the sound source increases to the speed of the sound waves themselves, the waves, not being able to get out of each other’s way, are forced together. They eventually merge, through constructive , into a single shock wave traveling at the speed of sound. This happens at the critical speed known as Mach. The shock waves radiate out from the sound source in the shape of a cone (see figure 6). When a person on the ground hears the sonic boom, the object that made it has long since passed.

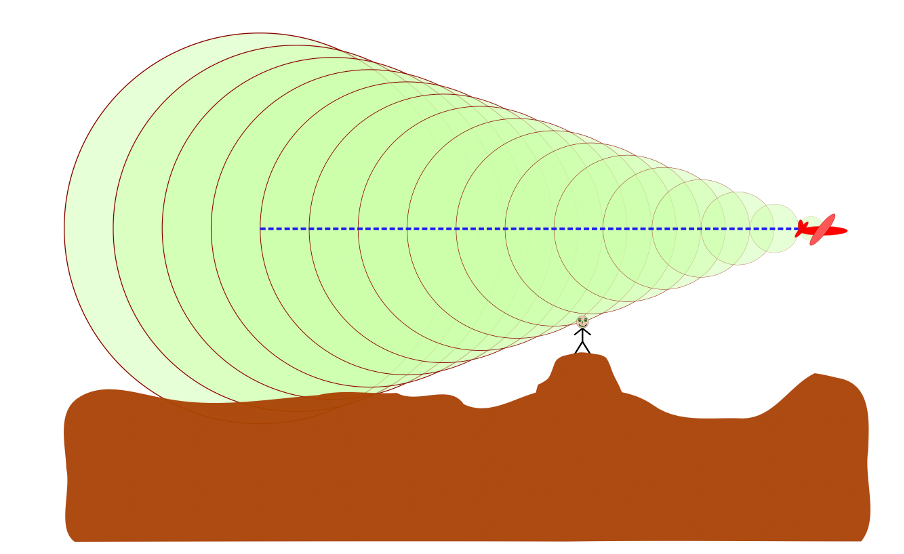
https://commons.wikimedia.org/wiki/File:Sonic_boom.svg – GNU — Figure 6: A sonic boom cone

Chuck Yeager of the United States Airforce was the first person to break the sound barrier. He flew a small airplane called the Bell X-1 (see figure 7) which is currently in the Smithsonian Air and Space Museum in Washington, DC.

Figure 7: The Bell X-1

Summary

In this unit you have learnt the following:

When a source emitting sound relative to a listener, the listener perceives a change in the frequency of the sound. This is called the Doppler effect.
If the source moves relatively towards the listener, the perceived frequency is higher.
If the source moves relatively away from the listener, the perceived frequency is lower.
The Doppler effect also occurs when a light emitting object moves relative to an observer.
If the object is moving relatively towards the observer, the light appears more blue (blueshift to higher frequency light).
If the object is moving relatively away from the observer, the light appears more red (redshift to lower frequency light).
The frequency of the wave (sound or light) perceived by the observer can be calculated using the formula $\scriptsize f_L=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S$ .

Suggested time to complete: 35 minutes

Question 1 adapted from NC(V) Level 4 Physical Science Paper 1 February 2019 question 10

A goods train sounds its horn as it approaches and passes through a station at a constant speed of 20 m·s−1. The horn has a frequency of 550 Hz. Assume the speed of sound in air is 344 m.s−1.
1. What is the frequency of the horn heard by people sitting on the station platform as the train approaches?
2. What is the frequency of the horn heard by the driver of the train?
3. The train passes through the station. The driver next sounds the horn when the train is travelling away from the station and has accelerated to a constant speed of $\scriptsize 30~\text{m.s}^{-1}$ . Will the frequency of the horn heard by the people sitting on the station platform INCREASE/DECREASE/REMAIN THE SAME? Support your answer with a calculation.

Question 2 adapted from NC(V) Level 4 Physical Science Paper 1 November 2019 question 10

The siren of a police car emits sound waves of wavelength 0.55 m. A stationary listener watches the police car approaching him at a constant velocity on a straight road. Assume that the speed of sound in air is 345 m.s−1.
1. How does the wavelength of the sound waves change as the police car approaches the listener? Only write down INCREASES, DECREASES or REMAINS THE SAME.
2. Calculate the observed frequency of the sound waves if the car moves toward him at a speed of $\scriptsize 120~\text{km/h}$ ?
3. How will the answer to question 2.b. change if the police car moves away from the listener at $\scriptsize 120~\text{km/h}$ ? Only write down INCREASES, DECREASES or REMAINS THE SAME.
A motorbike approaches you at an unknown speed. The sound of the bike’s engine has a frequency of 510 Hz, however you hear a frequency of 545 Hz. The speed of sound is 344 m.s−1.
1. Calculate the speed of the motorbike.
2. How will the sound change as the bike passes you? Explain this phenomenon in terms of the wavelength and frequency of the sound.

Question 4 adapted from Everything Science Grade 12 Exercise 6-2 question 4

A police car is driving towards a fleeing suspect at $\scriptsize \displaystyle \frac{v}{35}~\text{m.s}^{-1}$ , where $\scriptsize v$ is the speed of sound. The frequency of the police car’s siren is $\scriptsize 400~\text{Hz}$ . The suspect is running away at $\scriptsize \displaystyle \frac{v}{68}~\text{m.s}^{-1}$ . What frequency does the suspect hear?

The full solutions are at the end of the unit.

Exercise 1.1

$\scriptsize 85~\text{km/h}=23.61~\text{m.s}^{-1}$
We have been asked to calculate $\scriptsize f_L$ .
$\scriptsize \begin{align*} f_S&=812~\text{Hz}\\ v&=340~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ v_S&=-23.61~\text{m.s}^{-1}&&\text{source is moving towards observer}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left(\displaystyle \frac{340~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{340~\text{m.s}^{-1}-23.61~\text{m.s}^{-1}} \right )\cdot 812~\text{Hz}\\ &=872.59~\text{Hz} \end{align*}$
We have been asked to calculate $\scriptsize v_S$ .
$\scriptsize \begin{align*} f_L&=x~\text{Hz}\\ f_S&=1.15x~\text{Hz}\\ v&=340~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore v_S&=\displaystyle \frac{f_S}{f_L}\cdot (v\pm v_L)-v\\ \therefore v_S&=\displaystyle \frac{1.15x}{x}\cdot (340~\text{m.s}^{-1}+0~\text{m.s}^{-1})-340~\text{m.s}^{-1}\\ \therefore v_S&=1.15\cdot (340~\text{m.s}^{-1}+0~\text{m.s}^{-1})-340~\text{m.s}^{-1}\\ &=51~\text{m.s}^{-1} \end{align*}$
Therefore $\scriptsize v_S = 51~\text{m.s}^{-1}$ away from the observer.
We have been asked to calculate $\scriptsize v$ .
$\scriptsize \begin{align*} f_L&=2~335~\text{Hz}\\ f_S&=2~500~\text{Hz}\\ v_S&=22.5~\text{m.s}^{-1}&&\text{source moving away from observer}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore \displaystyle \frac{f_L}{f_S}&=\displaystyle \frac{v\pm v_L}{v\pm v_S}\\ \therefore \displaystyle \frac{v\pm v_L}{v\pm v_S}&=\displaystyle \frac{2~335~\text{Hz}}{2~500~\text{Hz}}=0.934\\ \therefore v+0~\text{m.s}^{-1}&=0.934\times (v+22.5~\text{m.s}^{-1})\\ \therefore v&=0.934v+21.015~\text{m.s}^{-1}\\ \therefore v-0.934v&=21.015~\text{m.s}^{-1}\\ \therefore v(1-0.934)&=21.015~\text{m.s}^{-1}\\ \therefore v&=318.41~\text{m.s}^{-1} \end{align*}$
.
1. We have been asked to calculate $\scriptsize v_L$ .
  $\scriptsize \begin{align*} f_L&=437.1\times 1.2~\text{Hz}=524.52~\text{Hz}\\ f_S&=437.1~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_S&=0~\text{m.s}^{-1}&&\text{source is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore v_L&=\displaystyle \frac{524.52~\text{Hz}}{437.1~\text{Hz}}\cdot (344~\text{m.s}^{-1}+0~\text{m.s}^{-1})-344~\text{m.s}^{-1}\\ &=68.8~\text{m.s}^{-1} \end{align*}$
2. We have been asked to calculate $\scriptsize f_L$ .
  $\scriptsize \begin{align*} f_S&=437.1~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_S&=0~\text{m.s}^{-1}&&\text{source is stationary}\\ v_L&=-68.8~\text{m.s}^{-1}&&\text{observer moving away from source}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left(\displaystyle \frac{344~\text{m.s}^{-1}-68.8~\text{m.s}^{-1}}{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}} \right )\cdot 437.1~\text{Hz}\\ &=349.68~\text{Hz} \end{align*}$

Back to Exercise 1.1

Unit 1: Assessment

.
1. We have been asked to calculate $\scriptsize f_L$ .
  $\scriptsize \begin{align*} f_S&=550~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ v_S&=-20~\text{m.s}^{-1}&&\text{source moving towards observer}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left(\displaystyle \frac{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}-20~\text{m.s}^{-1}} \right )\cdot 550~\text{Hz}\\ &=583.95~\text{Hz} \end{align*}$
2. The driver will hear the actual frequency of the horn – $\scriptsize 550~\text{Hz}$ .
3. The frequency of the horn for the people will decrease.
  $\scriptsize \begin{align*} f_S&=550~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ v_S&=30~\text{m.s}^{-1}&&\text{source moving away from observer}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left(\displaystyle \frac{344~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{344~\text{m.s}^{-1}+30~\text{m.s}^{-1}} \right )\cdot 550~\text{Hz}\\ &=505.88~\text{Hz} \end{align*}$
.
1. Increases
2. $\scriptsize 120~\text{km/h}=33.33~\text{m.s}^{-1}$
  $\scriptsize \begin{align*} v&=f\times \lambda\\ \therefore f&=\displaystyle \frac{v}{\lambda}=\displaystyle \frac{345~\text{m.s}^{-1}}{0.55~\text{m}}=627.27~\text{Hz}\end{align*}$
  We have been asked to calculate $\scriptsize f_L$ .
  $\scriptsize \begin{align*} f_S&=627.27~\text{Hz}\\ v&=345~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1} && \text{observer is stationary}\\ v_S&=-33.33~\text{m.s}^{-1} && \text{source moving towards observer}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore f_L&=\left(\displaystyle \frac{345~\text{m.s}^{-1}+0~\text{m.s}^{-1}}{345~\text{m.s}^{-1}-33.33~\text{m.s}^{-1}} \right )\cdot 627.27~\text{Hz}\\ &=694.35~\text{Hz} \end{align*}$
3. Decreases
.
1. We have been asked to calculate $\scriptsize v_S$ .
  $\scriptsize \begin{align*} f_S&=510~\text{Hz}\\ v_L&=575~\text{Hz}\\ v&=344~\text{m.s}^{-1}\\ v_L&=0~\text{m.s}^{-1}&&\text{observer is stationary}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ \therefore v_S&=\displaystyle \frac{f_S}{f_L}\cdot(v\pm v_L)-v\\ \therefore v_S&=\displaystyle \frac{510~\text{Hz}}{575~\text{Hz}}\cdot(344~\text{m.s}^{-1}+0~\text{m.s}^{-1})-344~\text{m.s}^{-1}\\ &=38.89~\text{m.s}^{-1} \end{align*}$
2. As the bike passes and travels away, the sound waves will become more spread out. The listener will perceive a sound of a lower frequency and hence a sound with a lower pitch.
We have been asked to calculate $\scriptsize f_L$ . Both the car and the suspect are moving. It is clear that the car is moving towards the suspect. However, because the car is moving faster than the suspect, the suspect is also moving towards the car even though he is trying to run away.
$\scriptsize \begin{align*} f_S&=400~\text{Hz}\\ v&=v~\text{m.s}^{-1}\\ v_L&=\displaystyle \frac{v}{68}~\text{m.s}^{-1}&&\text{observer is moving towards source}\\ v_S&=-\displaystyle \frac{v}{35}~\text{m.s}^{-1}&&\text{source is moving towards observer}\\ f_L&=\left(\displaystyle \frac{v\pm v_L}{v\pm v_S} \right )\cdot f_S\\ &=\left(\displaystyle \frac{v+\displaystyle \frac{v}{68}}{v-\displaystyle \frac{v}{35}} \right )\cdot 400~\text{Hz}\\ &=\left( \displaystyle \frac{\displaystyle \frac{68v+v}{68}}{\displaystyle \frac{35v-v}{35}} \right )\cdot 400~\text{Hz}\\ &=\left(\displaystyle \frac{68v+v}{68}\times \displaystyle \frac{35v-v}{35} \right )\cdot 400~\text{Hz}\\ &=\left(\displaystyle \frac{2380v+35v}{2380v-60v} \right )\cdot 400~\text{Hz}\\ &=\left(\displaystyle \frac{v(2380+35)}{v(2380-60)} \right )\cdot 400~\text{Hz}\\ &=416.38~\text{Hz} \end{align*}$

Back to Unit 1: Assessment

Media Attributions

License

Icon for the Creative Commons Attribution 4.0 International License

National Curriculum (Vocational) Physical Science Level 4 by Dylan Busa is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Unit 1: The Doppler effect

Unit outcomes

What you should know

Introduction

Did you know?

The Doppler effect

Take note!

Activity 1.1: The Doppler effect

Note

Calculate the Doppler effect

Take note!

Take note!

Example 1.1

Example 1.2

Example 1.3

Note

Exercise 1.1

Applications of the Doppler effect

Sonic booms

Note

Did you know?

Summary

Suggested time to complete: 35 minutes

Exercise 1.1

Unit 1: Assessment

Media Attributions

License

Share This Book

Unit outcomes

What you should know

Introduction

Did you know?

The Doppler effect

Take note!

Activity 1.1: The Doppler effect

Note

Calculate the Doppler effect

Take note!

Take note!

Example 1.1

Example 1.2

Example 1.3

Note

Exercise 1.1

Applications of the Doppler effect

Sonic booms

Note

Did you know?

Summary

Unit 1: Assessment

Suggested time to complete: 35 minutes

Unit 1: Solutions

Exercise 1.1

Unit 1: Assessment

Media Attributions

License

Share This Book