Unit 1 outcomes

By the end of this unit you will be able to:

• Define and calculate momentum.
• Calculate the change of momentum of an object.
• Define impulse ([latex]\scriptsize {{F}_{{nett}}}\cdot t[/latex]) as the change in momentum and use [latex]\scriptsize {{F}_{{nett}}}\cdot \Delta t=m\cdot \Delta v[/latex] for calculations and problem solving.

What you should know

Before you start this unit, make sure you can:

• Define and work with vector quantities. Refer to level 2 subject outcome 2.1 unit 3 if you need help with this.
• Identify and apply principles of force. Refer to level 2 subject outcome 2.2 if you need help with this.
• Describe, analyse and apply principles of concurrent forces. Refer to level 3 subject outcome 2.2 if you need help with this.

Introduction

What would you rather be hit by a tennis ball travelling at [latex]\scriptsize 145\,\text{km/h}[/latex] or a cricket ball travelling at [latex]\scriptsize 50\,\text{km/h}[/latex]? In considering this, you may think that the tennis ball would be the better option because it is lighter and softer. However, it is travelling at about three times the speed.

Our experience of the real world and intuition tell us that heavier things hit harder. When a fly lands on your arm you hardly notice it. When a dog jumps on you, you feel it. The fly is light, and the dog is heavy.

However, our experience and intuition also tell us that faster things hit harder. A car travelling at [latex]\scriptsize 10\,\text{km/h}[/latex] is going to do far less damage if driven into a wall than the same car travelling at [latex]\scriptsize 100\,\text{km/h}[/latex] driven into the same wall.

Which property, the mass of an object or its velocity, matters more when considering the force it can exert?

Momentum

Moving objects can exert a force on other objects as a result of their momentum. Momentum can be simply defined as mass in motion. Every moving object, from stars to electrons, has momentum. If it is not moving, it has no momentum.

We define momentum ([latex]\scriptsize p[/latex]) as the mass of an object multiplied by its velocity. Therefore, [latex]\scriptsize p=m\cdot v[/latex].

As velocity is a vector, momentum is also a vector. Whenever we calculate momentum, we need to note its direction.

This means that momentum is directly proportional to both mass and velocity. If you increase either mass or velocity, you increase momentum. If you double an object’s velocity, you double its momentum. If you double an object’s mass, you double its momentum. If you double both an object’s velocity and mass, you quadruple its momentum.

As mass in measured in [latex]\scriptsize \text{kg}[/latex] and velocity is measured in [latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex], momentum has units of [latex]\scriptsize \text{kg}\text{.m}\text{.}{{\text{s}}^{{-1}}}[/latex].

Take note!

[latex]\scriptsize p=m\cdot v[/latex]
Momentum ([latex]\scriptsize p[/latex]) has units [latex]\scriptsize \text{kg}\text{.m}\text{.}{{\text{s}}^{{-1}}}[/latex].
Momentum is a vector quantity.

Example 1.1

A cricket ball of mass [latex]\scriptsize \text{163}\ \text{g}[/latex] is hit towards the boundary at [latex]\scriptsize 30\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. What is the momentum of the ball?

Solution

Step 1: Identify the information that has been given

• The mass of the cricket ball: [latex]\scriptsize \text{163}\ \text{g}=0.163\ \text{kg}[/latex] (remember that all quantities need to be expressed in SI with SI units).
• The velocity of the cricket ball: [latex]\scriptsize 30\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]

We need to calculate the momentum of the ball. We will define the positive direction as towards the boundary.

Step 2: Do the calculation

[latex]\scriptsize p=m\cdot v=0.163\ \text{kg}\times 30\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=4.89\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]

Step 3: Write the final answer

The cricket ball’s momentum is [latex]\scriptsize 4.89\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] towards the boundary.

Example 1.2

Example adapted from Everything Science Grade 12 Worked Example 3 page 24

The centre of the moon is approximately [latex]\scriptsize 384\ 400\ \text{km}[/latex] away from the centre of the earth and orbits the earth in [latex]\scriptsize 27.3\ \text{days}[/latex] days. If the moon has a mass of [latex]\scriptsize 7.35\times {{10}^{{22}}}\ \text{kg}[/latex], what is the magnitude of its momentum? Assume that the moon’s orbit is circular.

Solution

Step 1: Identify the information that has been given

• The mass of the moon: [latex]\scriptsize 7.35\times {{10}^{{22}}}\ \text{kg}[/latex]
• The distance of the moon from earth: [latex]\scriptsize 384\ 400\ \text{km}=384\ 400\ 000\ \text{m}[/latex]
• The duration of orbit: [latex]\scriptsize 27.3\ \text{days}=27.3\times 24\ \text{hrs/day}\times 60\ \text{min/hr}\times 60\ \text{s/min}=2\ 358\ 720\ \text{s}[/latex]

We need to calculate the magnitude of the momentum of the moon. We do not need to worry about its direction in this case. We are told to assume that the moon’s orbit is circular.

Step 2: Do the calculation

If the moon’s orbit is circular, then we can assume that its distance from the earth is constant and equal to the radius of this orbit. With the orbital radius, we can calculate the orbital circumference.
[latex]\scriptsize \text{Circumference}=2\pi r=2\times \pi \times 384\ 400\ 000\;\text{m}=2\;415\;256\;432.08\;\text{m}[/latex]

The moon covers this distance in [latex]\scriptsize 2\ 358\;720\ \text{s}[/latex]. Therefore, we can calculate the magnitude of the moon’s velocity.
[latex]\scriptsize v=\displaystyle \frac{{\Delta s}}{{\Delta t}}=\displaystyle \frac{{2\ 415\ 432.08\ \text{m}}}{{2\ 358\ 720\ \text{s}}}=1\ 023.97\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]

Now we can calculate the magnitude of the moon’s momentum.
[latex]\scriptsize p=m\cdot v=7.35\times {{10}^{{22}}}\ \text{kg}\times 1\ 023.97\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=7.53\times {{10}^{{25}}}\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]

Step 3: Write the final answer

The magnitude of the moon’s momentum is [latex]\scriptsize 7.53\times {{10}^{{25}}}\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].

Exercise 1.1

Questions 1, 2 and 3 adapted from Everything Science Grade 12 Exercise 2 – 1 page 29

1. The fastest recorded delivery for a cricket ball is [latex]\scriptsize 161.3\ \text{km/h}[/latex], bowled by Shoaib Akhtar of Pakistan during a match against England in the 2003 Cricket World Cup, held in South Africa. Calculate the ball’s momentum if it had a mass of [latex]\scriptsize 160\ \text{g}[/latex].
2. The fastest tennis service by a man is [latex]\scriptsize 246.2\ \text{km/h}[/latex] by Andy Roddick of the United States of America during a match in London in 2004. Calculate the ball’s momentum if it had a mass of [latex]\scriptsize 58\ \text{g}[/latex].
3. Would you rather face the bowling of Shoaib Akhtar or the serve of Andy Roddick? Explain.

The full solutions can be found at the end of the unit.

A change in momentum

When a cricket ball hits you, it slows down. If it slows down, then its momentum changes. Whenever an object hits another object there is a change in momentum, often because of a change in the velocity of the object but, sometimes, also because of a change in the mass of the object.

It stands to reason that the change in an object’s momentum is calculated as its final momentum minus its initial momentum. That is, after all what ‘change’ means. Therefore, [latex]\scriptsize \Delta p={{p}_{f}}-{{p}_{i}}[/latex].

We can write this in terms of mass and velocity as [latex]\scriptsize \Delta p={{m}_{f}}\cdot {{v}_{f}}-{{m}_{i}}\cdot {{v}_{i}}[/latex]. If mass is constant (which it almost always is) we can simplify this as follows:
[latex]\scriptsize \begin{align*}\Delta p & ={{m}_{f}}\cdot {{v}_{f}}-{{m}_{i}}\cdot {{v}_{i}}\\\therefore \Delta p & =m\cdot {{v}_{f}}-m\cdot {{v}_{i}}\\\therefore \Delta p & =m\cdot \Delta v\end{align*}[/latex]

Because momentum is a vector quantity, we can illustrate the change in momentum using the techniques of vector addition. We will deal with cases in only one dimension.

An object bouncing off a wall or the floor

Figure 1 shows the case of a ball bouncing off a wall. The total change in the object’s momentum is given by the vector drawn from the end of the initial momentum vector to the end of the final momentum vector.

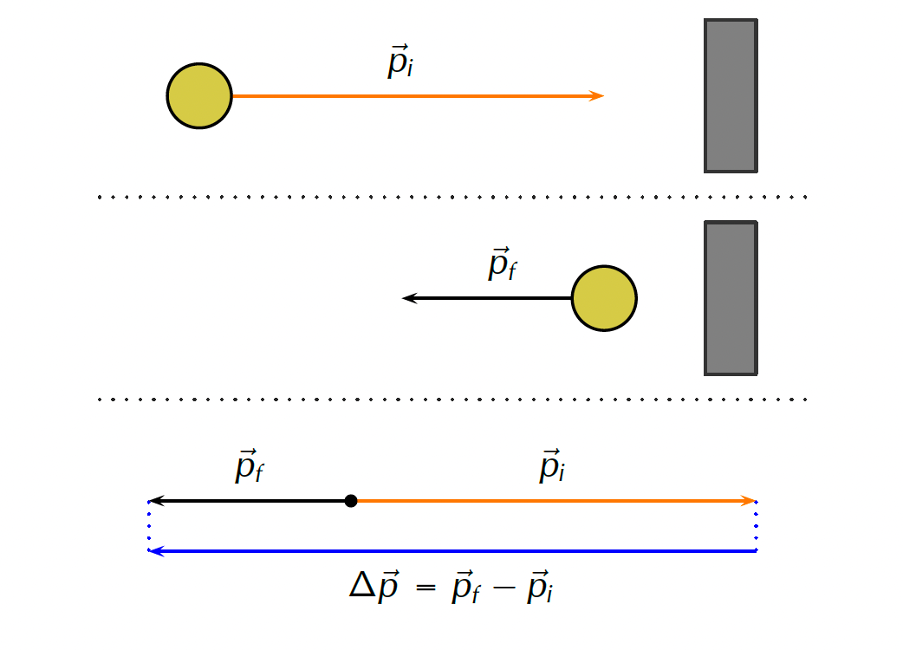
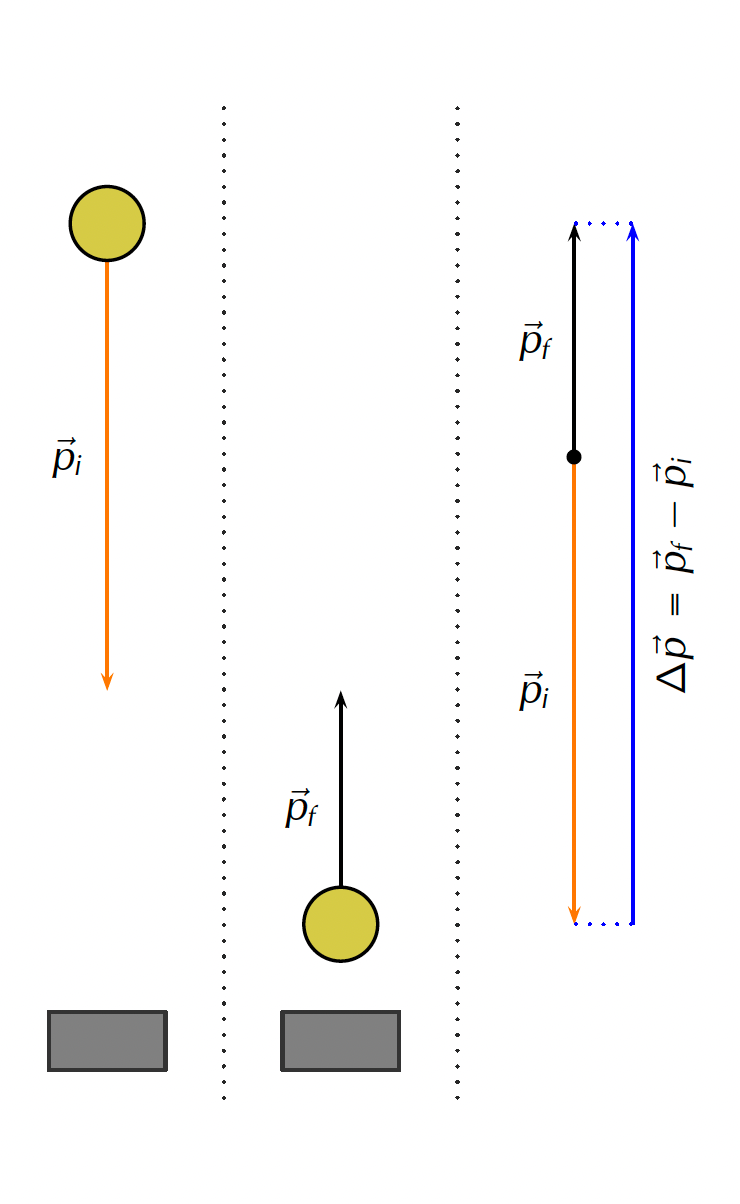
Figure 2 shows a similar situation of a ball bouncing off the floor. Note, however, that to keep things simple, we will ignore the effects of gravity.

Example 1.3

A netball ball with a mass of [latex]\scriptsize 425\ \text{g}[/latex] is thrown against a wall perpendicularly with a velocity of [latex]\scriptsize 12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. If it rebounds at a velocity of [latex]\scriptsize 9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex], calculate its change in momentum.

Solution

Step 1: Identify the information that has been given

• The mass of the netball: [latex]\scriptsize 425\ \text{g}=0.425\ \text{kg}[/latex]
• The initial velocity of the netball: [latex]\scriptsize 12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The final velocity of the netball: [latex]\scriptsize -9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] (We will define towards the wall as the positive direction)

We need to calculate the change in the momentum of the netball.

Step 2: Do the calculation

[latex]\scriptsize \displaystyle \begin{align*}\Delta p&=m\cdot \Delta v\\&=m({{v}_{f}}-{{v}_{i}})\\&=0.425\ \text{kg}(-9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})\\&=0.425\ \text{kg}\times -21\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\&=-8.925\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]

Step 3: Write the final answer

The change in the netball’s momentum is [latex]\scriptsize -8.925\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] away from the wall.

If we calculate the momentum of the netball in example 1.3 before and after it hits the wall, we get the following answers:
[latex]\scriptsize {{p}_{i}}=m\cdot {{v}_{i}}=0.425\ \text{kg}\times 12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=5.1\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] towards the wall
[latex]\scriptsize {{p}_{f}}=m\cdot {{v}_{f}}=0.425\ \text{kg}\times -9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=-3.825\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] or [latex]\scriptsize 3.825\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] away from the wall

It may seem strange that the change in momentum is greater than either the initial or final momentum but, if you think about it, this makes sense. The netball had [latex]\scriptsize 5.1\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] of momentum towards the wall to start with. It then had [latex]\scriptsize 3.825\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] of momentum away from the wall. Its change in momentum had to be enough to completely reverse the initial moment AND give it some momentum in the reverse direction.

An object continues but more slowly

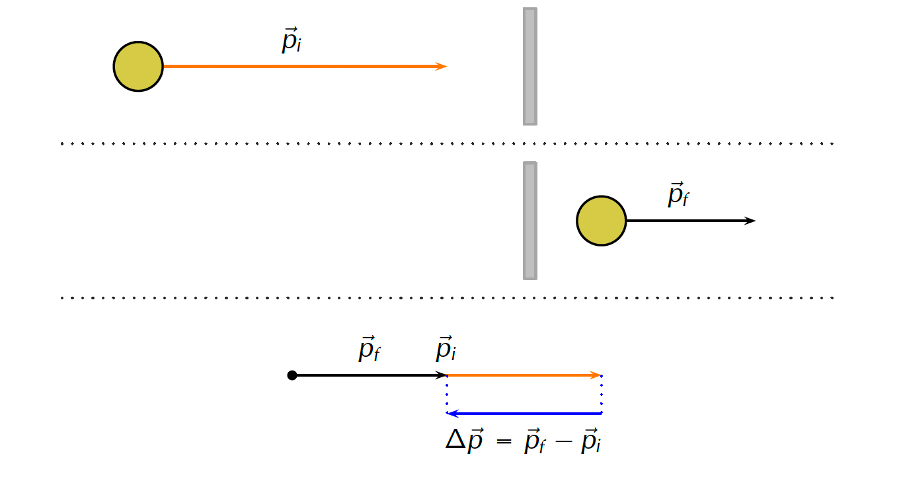
Sometimes, when an object collides with something it does not bounce back but continues in its original direction, only more slowly. A bullet passing through a target is an example. Figure 3 shows such a case.

Example 1.4

A [latex]\scriptsize 40\ \text{g}[/latex] bullet is fired at [latex]\scriptsize 595\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. It strikes a stationary cement block perpendicular to its surface. The bullet goes through the block and comes out on the other side at [latex]\scriptsize 210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. Calculate the change in momentum of the bullet.

Solution

Step 1: Identify the information that has been given

• The mass of the bullet: [latex]\scriptsize 40\ \text{g}=0.04\ \text{kg}[/latex]
• The initial velocity of the bullet: [latex]\scriptsize 595\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The final velocity of the bullet: [latex]\scriptsize 210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• Notice that both velocities are in the same direction so they both have the same sign.

We need to calculate the change in the momentum of the bullet. We will define the bullet’s initial flight towards the block as the positive direction.

Step 2: Do the calculation

[latex]\scriptsize \begin{align*}\Delta p&=m\cdot \Delta v\\&=m({{v}_{f}}-{{v}_{i}})\\&=0.04\ \text{kg}\times (210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-595\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})\\&=0.04\ \text{kg}\times \left(-385\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\right) \\&=-15.4\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]

Step 3: Write the final answer

The change in the bullet’s momentum is [latex]\scriptsize 15.4\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the opposite direction to the bullet’s flight.

It might seem strange that even though the bullet continued travelling in the same direction, we still get a change in momentum in the opposite direction. However, after hitting the block, the bullet was travelling more slowly (i.e. with less momentum), hence the change of momentum is clearly negative.

An object continues but faster

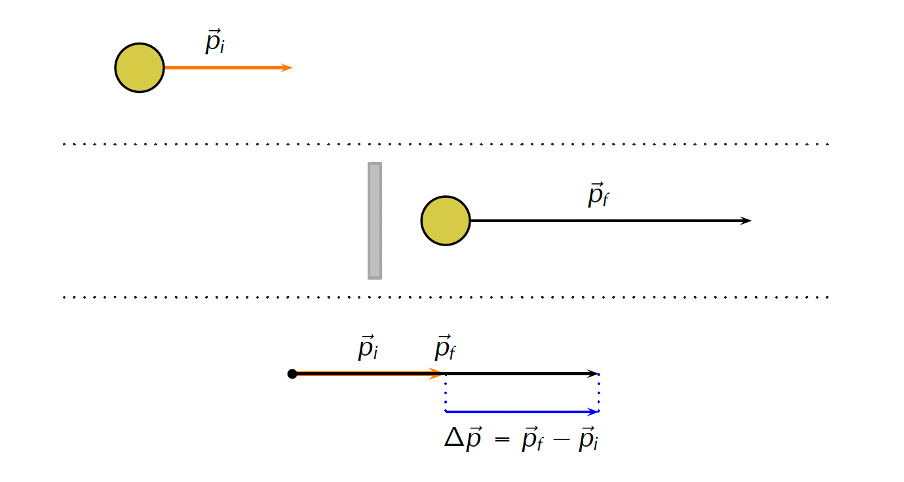
Sometimes objects that are already moving are given a push to move even faster. Think of a soccer ball travelling towards the goal when a player comes up behind it and gives it another kick. Figure 4 illustrates this situation.

Example 1.5

In the game of squash, a player may hit a ball that has bounced off the back glass. A regulation squash ball weighs [latex]\scriptsize 24\ \text{g}[/latex]. In a game, the ball bounces off the back glass and travels towards the front at [latex]\scriptsize 1.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] before a player hits it with her racquet. After being hit towards the front wall, the ball is moving at [latex]\scriptsize 32\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. What is the change in momentum of the ball?

Solution

Step 1: Identify the information that has been given.

• The mass of the ball: [latex]\scriptsize 24\ \text{g}=0.024\ \text{kg}[/latex]
• The initial velocity of the ball: [latex]\scriptsize 1.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The final velocity of the ball: [latex]\scriptsize 32\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]

We need to calculate the change in the momentum of the ball. We will define travelling towards the front wall as the positive direction.

Step 2: Do the calculation

[latex]\scriptsize \begin{align*}\Delta p&=m\cdot \Delta v\\&=m({{v}_{f}}-{{v}_{i}})\\&=0.024\ \text{kg}\times (32\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-1.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})\\&=0.024\ \text{kg}\times 30.8\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\&=0.7392\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]

Step 3: Write the final answer

The change in the ball’s momentum is [latex]\scriptsize 0.74\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] towards the front wall.

In this case, the ball’s momentum after being hit was greater than before it was hit. Therefore, the change in momentum is positive and in the direction of the front wall.

Exercise 1.2

1. A basketball player bounces a basketball on the ground. The mass of the ball is [latex]\scriptsize 590\ \text{g}[/latex]. Its velocity down towards the ground is [latex]\scriptsize 7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] and it bounces up with a velocity of [latex]\scriptsize 4.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. What is its change in momentum? Ignore the effects of gravity.
2. The change in momentum of a [latex]\scriptsize 2.2\ \text{kg}[/latex] brick crashing through a pane of glass is [latex]\scriptsize 5.73\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. If its velocity immediately after hitting the glass is [latex]\scriptsize 13\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex], what is its velocity just before hitting the glass?

The full solutions can be found at the end of the unit.

Impulse

Why do cars have airbags? What do they do? How do they improve safety? To answer these questions, we need to step back for a moment.

We know that an object in motion has momentum. We also know from experience that when a moving object (one with momentum) hits us, we feel it. It applies a force. However, Newton’s third law of motion reminds us that every action has an equal and opposite reaction. In other words, if object A applies a force on object B, then object B applies an equal but opposite force on object A. We will learn more about this in the next unit.

Think of a hard ball like a cricket ball. As it hits your hand, it has momentum and applies a force to your hand. Your hand also applies a force to the ball which causes it to slow down, stop and lose all momentum. Hold this thought.

Do you remember Newton’s second law of motion? It says that the force applied to an object is equal to its mass multiplied by its acceleration.

It must be said that while [latex]\scriptsize {{F}_{{nett}}}=m\cdot a[/latex] is correct and an accurate description of Newton’s second law, it is not quite how Newton described it. He described it in terms of momentum.
[latex]\scriptsize \displaystyle \begin{align*}&{{f}_{{nett}}}=m\cdot a\\&\text{But}\ a=\displaystyle \frac{{\Delta v}}{t}=\displaystyle \frac{{v-u}}{t}\text{ or } \displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{t}\\&\text{So}\ {{F}_{{nett}}}=m\cdot \displaystyle \frac{{({{v}_{f}}-{{v}_{i}})}}{t}\\&\text{But}\ m({{v}_{f}}-{{v}_{i}})=\Delta p\\&\text{Therefore}\ {{F}_{{nett}}}=\displaystyle \frac{{\Delta p}}{t}\end{align*}[/latex]

We can rewrite this as [latex]\scriptsize \Delta p={{F}_{{nett}}}\cdot t[/latex]. We call [latex]\scriptsize {{F}_{{nett}}}\cdot t[/latex] impulse. This means that [latex]\scriptsize \Delta p={{F}_{{nett}}}\cdot t=\text{impulse}[/latex].

Take note!

Impulse is the product of the net force and the time interval for which the force acts.
[latex]\scriptsize \text{impulse}=\Delta p={{F}_{{nett}}}\cdot \Delta t[/latex]

We can also say that:
[latex]\scriptsize {{F}_{{nett}}}=\displaystyle \frac{{\Delta p}}{{\Delta t}}[/latex]

But why do we care about impulse? If we need to change the momentum of a moving object, we can either apply a larger force for a shorter time or a smaller force for a longer time. In the case of catching a cricket ball, this matters.

Cricket players are taught to hold their hands out to the ball and gradually bring the ball into their body. They do this to increase the time over which their hands apply the force needed to reduce the ball’s momentum to zero. The longer they can make this time, the less force they need to apply to the ball (and hence the ball will apply to their hands) and the less it will hurt. Cricketers call this catching the ball with ‘soft hands’.

The same is true if you ever need to catch an egg. You want to reduce the force needed to change the egg’s momentum to zero, so you want to use ‘soft hands’ applying that force over the longest time possible.

We can now answer our initial question about air bags. Air bags reduce the effect of the force experienced by a person during an accident. If the person is stopped by a collision with the windshield, the time of the impact would be short and so a large force would need to be exerted. If instead of hitting the windshield, the person hits an air bag, then the time of the impact is increased which results in a decrease in the force.

For a constant change in momentum, like bringing a person inside a car to rest, [latex]\scriptsize {{F}_{{nett}}}\cdot \Delta t[/latex] is constant. Therefore, if [latex]\scriptsize t[/latex] is increased, the force on the body is decreased.

Example 1.6

Waste pickers are pulling a trolley of mass [latex]\scriptsize 350\ \text{kg}[/latex]. They pull it with a resultant [latex]\scriptsize 15\ \text{N}[/latex] force. How long does it take for them to increase the trolley’s velocity from [latex]\scriptsize 3\ \text{km/h}[/latex] to [latex]\scriptsize 5\ \text{km/h}[/latex] in the same direction?

Solution

Step 1: Identify the information that has been given

• The mass of the trolley: [latex]\scriptsize 350\ \text{kg}[/latex]
• The initial velocity of the trolley: [latex]\scriptsize 3\ \text{km/h}=0.833\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The final velocity of the trolley: [latex]\scriptsize 5\ \text{km/h}=1.389\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The resultant force: [latex]\scriptsize 15\ \text{N}[/latex]

We need to calculate the length of time the resultant force must be applied to accelerate the trolley from [latex]\scriptsize 3\ \text{km/h}[/latex] to [latex]\scriptsize 5\ \text{km/h}[/latex]. We will define the initial direction of the trolley as the positive direction.

Step 2: Do the calculation

[latex]\scriptsize \begin{align*}{{F}_{{nett}}} & =\displaystyle \frac{{\Delta p}}{{\Delta t}}\\\therefore {{F}_{{nett}}} & =\displaystyle \frac{{m\cdot ({{v}_{f}}-{{v}_{i}})}}{{\Delta t}}\\\therefore \Delta t & =\displaystyle \frac{{m\cdot ({{v}_{f}}-{{v}_{i}})}}{{{{F}_{{nett}}}}}\\ & =\displaystyle \frac{{350\ \text{kg}\times (1.389\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-0.833\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{15\ \text{N}}}\\ & =\displaystyle \frac{{350\ \text{kg}\times 0.556\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{15\ \text{N}}}\\ & =12.97\ \text{s}\end{align*}[/latex]

Step 3: Write the final answer

It takes [latex]\scriptsize 12.97\ \text{s}[/latex] for the waste pickers to accelerate the trolley from [latex]\scriptsize 3\ \text{km/h}[/latex] to [latex]\scriptsize 5\ \text{km/h}[/latex].

Example 1.7

A goalkeeper catches a soccer ball travelling at [latex]\scriptsize 58\ \text{km/h}[/latex] in [latex]\scriptsize 1.2\ \text{s}[/latex]. If the ball has a mass of [latex]\scriptsize 435\ \text{g}[/latex], what force does he apply to the ball?

Solution

Step 1: Identify the information that has been given

• The mass of the ball: [latex]\scriptsize 435\ \text{g}=0.435\ \text{kg}[/latex]
• The initial velocity of the ball: [latex]\scriptsize 58\ \text{km/h}=16.11\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The final velocity of the ball: [latex]\scriptsize 0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
• The time over which the force is applied: [latex]\scriptsize 1.2\ \text{s}[/latex]

We need to calculate the resultant force that must be applied to catch (i.e. stop) the ball. We will define the initial direction of the ball as the positive direction.

Step 2: Do the calculation

[latex]\scriptsize \begin{align*}{{F}_{{nett}}} & =\displaystyle \frac{{\Delta p}}{{\Delta t}}\\\therefore {{F}_{{nett}}} & =\displaystyle \frac{{m\cdot ({{v}_{f}}-{{v}_{i}})}}{{\Delta t}}\\ & =\displaystyle \frac{{0.435\ \text{kg}\times (0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-16.11\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{1.2\ \text{s}}}\\ & =\displaystyle \frac{{0.435\ \text{kg}\times (-16.11\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{1.2\ \text{s}}}\\ & =-5.84\ \text{N}\end{align*}[/latex]

Step 3: Write the final answer

The goalkeeper will need to apply a force of [latex]\scriptsize 5.84\ \text{N}[/latex] in the opposite direction to the ball’s initial motion to catch it.

We can plot the force applied to an object against time to produce a force-time graph. These are similar to the displacement-time, velocity-time and acceleration-time graphs of motion we learnt about in level 3 subject outcome 2.1 unit 2 and 3. Figures 5 shows two examples of these graphs.

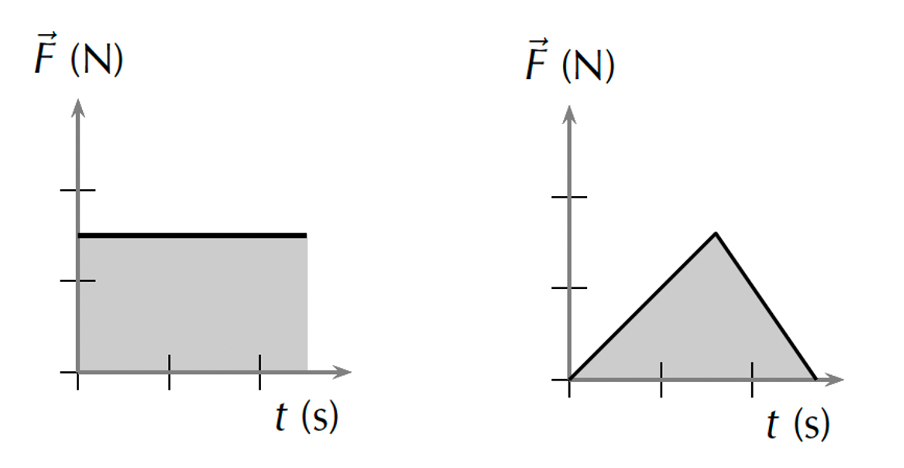
What do you think the area under a force-time graph represents?

If we calculated the shaded area under either of the graphs in figure 5, the units would be N.s. In other words, the shaded areas represent impulse ([latex]\scriptsize \text{impulse}={{F}_{{nett}}}\cdot \Delta t[/latex]).

Example 1.8

Question adapted from Everything Science Grade 12 Worked Example 17 page 56

Analyse the force-time graph provided and answer the following questions:

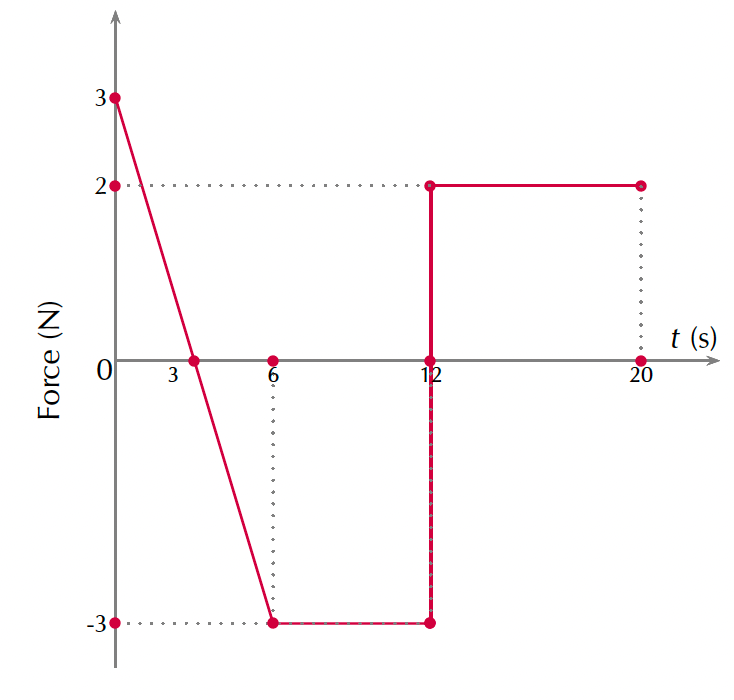
1. What is the impulse for the interval [latex]\scriptsize 0\ \text{s}[/latex] to [latex]\scriptsize 3\ \text{s}[/latex]?
2. What is the impulse for the interval [latex]\scriptsize 3\ \text{s}[/latex] to [latex]\scriptsize 6\ \text{s}[/latex]?
3. What is the change in momentum for the interval [latex]\scriptsize 0\ \text{s}[/latex] to [latex]\scriptsize 6\ \text{s}[/latex]?
4. What is the impulse for the interval [latex]\scriptsize 6\ \text{s}[/latex] to [latex]\scriptsize 20\ \text{s}[/latex]?

Solutions

1. We need to calculate the impulse of the interval [latex]\scriptsize 0\ \text{s}[/latex] to [latex]\scriptsize 3\ \text{s}[/latex]. In other words, we need to calculate the area under the graph from [latex]\scriptsize t=0\ \text{s}[/latex] to [latex]\scriptsize t=3\ \text{s}[/latex].
   
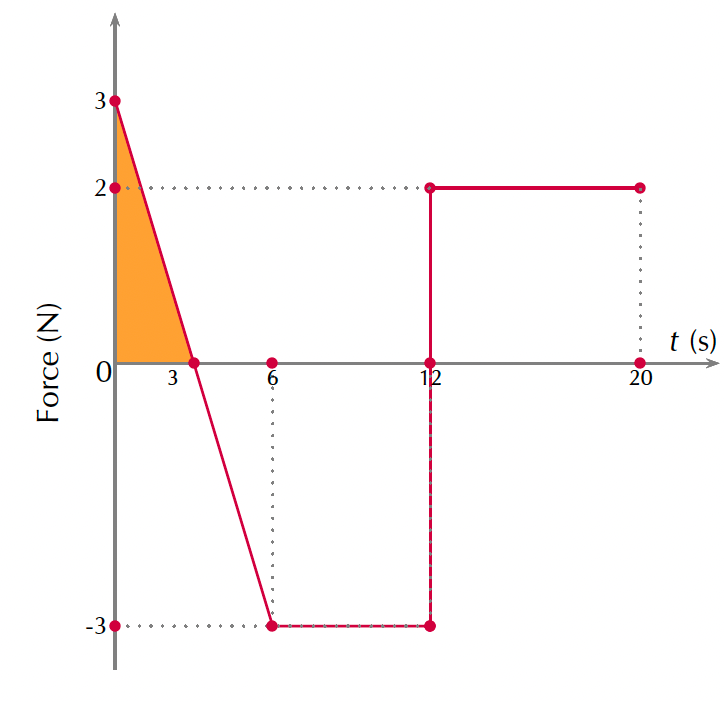
   [latex]\scriptsize \text{Area}=\displaystyle \frac{1}{2}\times \text{base}\times \text{height}=\displaystyle \frac{1}{2}\times 3\ \text{s}\times 3\ \text{N}=4.5\ \text{N}\text{.s}[/latex]
   .
   The impulse is [latex]\scriptsize 4.5\ \text{N}\text{.s}[/latex] in the positive direction (the area is above the axis).
2. We need to calculate the impulse of the interval [latex]\scriptsize 3\ \text{s}[/latex] to [latex]\scriptsize 6\ \text{s}[/latex]. In other words, we need to calculate the area under the graph from [latex]\scriptsize t=3\ \text{s}[/latex] to [latex]\scriptsize t=6\ \text{s}[/latex].
   
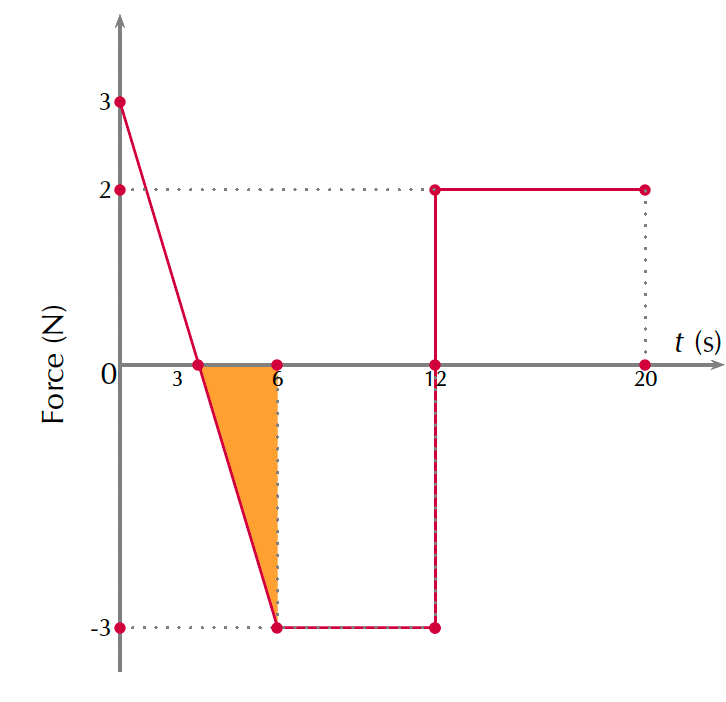
   [latex]\scriptsize \text{Area}=\displaystyle \frac{1}{2}\times \text{base}\times \text{height}=\displaystyle \frac{1}{2}\times 3\ \text{s}\times (-3\ \text{N})=-4.5\ \text{N}\text{.s}[/latex]
   .
   The impulse is [latex]\scriptsize 4.5\ \text{N}\text{.s}[/latex] in the negative direction (the area is below the axis).
3. We need to calculate the change in momentum between [latex]\scriptsize 0\ \text{s}[/latex] and [latex]\scriptsize 6\ \text{s}[/latex].
   [latex]\scriptsize \begin{align*}\Delta p & =\text{impulse}\\\therefore \Delta p & =\text{impuls}{{\text{e}}_{{0-3}}}+\text{impuls}{{\text{e}}_{{3-6}}}=4.5\ \text{N}\text{.s}-4.5\ \text{N}\text{.s}=0\ \text{N}\text{.s}\end{align*}[/latex]
   .
   The total change in momentum is [latex]\scriptsize 0\ \text{N}\text{.s}[/latex] (or [latex]\scriptsize 0\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{-1}}}[/latex])
4. We need to calculate the impulse of the interval [latex]\scriptsize 6\ \text{s}[/latex] to [latex]\scriptsize 20\ \text{s}[/latex]. In other words, we need to calculate the area under the graph from [latex]\scriptsize t=6\ \text{s}[/latex] to [latex]\scriptsize t=20\ \text{s}[/latex].
   
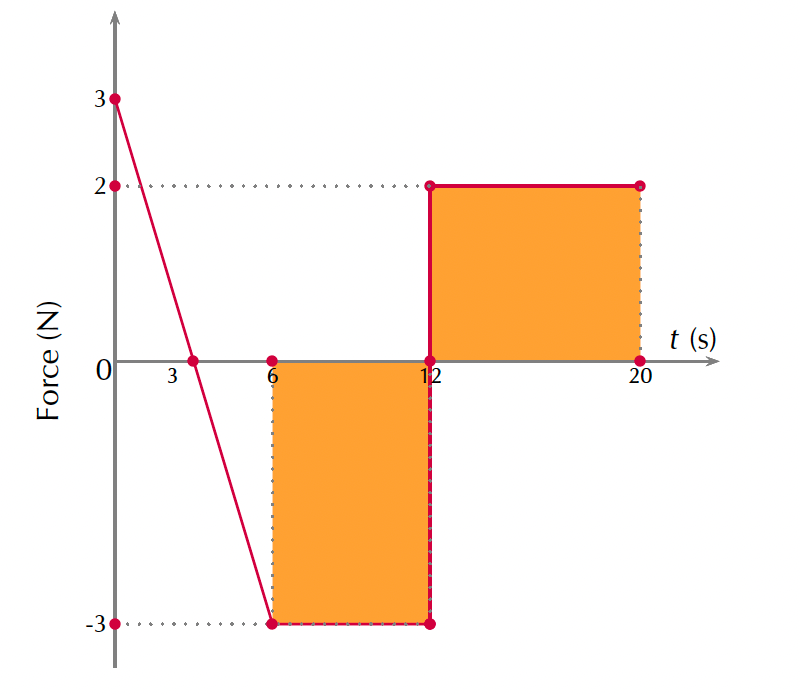
   [latex]\scriptsize \text{Area}=\text{base}\times \text{height}=6\ \text{s}\times (-3\ \text{N)+8}\ \text{s}\times 2\ \text{N}=-18\ \text{N}\text{.s}+16\ \text{N}\text{.s}=-2\ \text{N}\text{.s}[/latex]
   .
   The impulse is [latex]\scriptsize 2\ \text{N}\text{.s}[/latex] in the negative direction. Therefore, the total change in momentum is [latex]\scriptsize 2\ \text{N}\text{.s}[/latex] in the negative direction.

Exercise 1.3

1. A radio-controlled car (car A) of mass [latex]\scriptsize 1.3\ \text{kg}[/latex] is moving clockwise around a track at [latex]\scriptsize 12\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]. It collides head-on with another radio-controlled car (car B) of mass [latex]\scriptsize 1.12\ \text{kg}[/latex] moving at a velocity of [latex]\scriptsize 1.04\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex] in the opposite direction. After the collision car A moves with a velocity of [latex]\scriptsize 1.6\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex] in the clockwise direction and car B rebounds (travels in the opposite direction to before) at [latex]\scriptsize 11.03\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex].
   1. Calculate the change in momentum for each toy car.
   2. Determine the impulse for each toy car.
   3. Determine the duration of the collision if the magnitude of the force exerted by each toy car is [latex]\scriptsize 16.2\ \text{N}[/latex].
2. A bullet of mass [latex]\scriptsize 22\ \text{g}[/latex] strikes a target at [latex]\scriptsize 330\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] and exits at [latex]\scriptsize 210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. The tip of the bullet takes [latex]\scriptsize 0.00013\ \text{s}[/latex] to pass through the target. Determine:
   1. The change of momentum of the bullet.
   2. The impulse of the bullet.
   3. The magnitude of the force experienced by the bullet.
3. A piece of modelling clay with a mass of [latex]\scriptsize 400\ \text{g}[/latex] is thrown against a wall with a velocity of [latex]\scriptsize 9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. It sticks to the wall. Calculate:
   1. The impulse of the clay on the wall.
   2. The force exerted by the clay on the wall if it is in contact with the wall for [latex]\scriptsize 0.25\ \text{s}[/latex] before it comes to rest.

The full solutions can be found at the end of the unit.

Summary

In this unit you have learnt the following:

• That momentum is mass in motion. Every moving object has momentum.
• We define momentum ([latex]\scriptsize p[/latex]) as the mass of an object multiplied by its velocity. Therefore, [latex]\scriptsize p=m\cdot v[/latex].
• Momentum is a vector.
• Momentum has units of [latex]\scriptsize \text{kg}\text{.m}\text{.}{{\text{s}}^{{-1}}}[/latex].
• The change in momentum is [latex]\scriptsize \Delta p=m\cdot \Delta v[/latex].
• [latex]\scriptsize \Delta p={{F}_{{nett}}}\cdot t=\text{impulse}[/latex]
• The area under a force-time graph represents impulse.

Unit 1: Assessment

Suggested time to complete: 35 minutes

Question 1 adapted from Everything Science Grade 12 Worked example 16 page 55

1. A cricket ball weighing [latex]\scriptsize 156\ \text{g}[/latex] is moving at [latex]\scriptsize \text{54}\ \text{km/h}[/latex] towards a batsman. It is hit by the batsman back towards the bowler at [latex]\scriptsize 36\ \text{km/h}[/latex]. Calculate:
   1. The ball’s impulse.
   2. The average force exerted by the bat if the ball is in contact with the bat for [latex]\scriptsize 0.13\ \text{s}[/latex].
2. A squash player hits the ball (mass [latex]\scriptsize 24\ \text{g}[/latex]) and it strikes her opponent at [latex]\scriptsize 105\ \text{km/h}[/latex] on the leg. It rebounds at [latex]\scriptsize 43\ \text{km/h}[/latex].
   1. Calculate the change in the momentum of the ball.
   2. What is the impulse of the ball on the player?
   3. Calculate the magnitude of the force exerted by the ball on the player if the collision takes [latex]\scriptsize 0.017\ \text{s}[/latex].
3. Modern cars are deliberately designed with a front crumple zone – an area designed to deliberately crumple in a head on collision Why is this a good idea?

The full solutions can be found at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. [latex]\scriptsize m=160\ \text{g}=0.160\ \text{kg}[/latex]
   [latex]\scriptsize v=161.3\ \text{km/h}=44.81\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   Define the direction in which the ball is bowled as positive.
   [latex]\scriptsize p=m\cdot v=0160\ \text{kg}\times 44.81\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=7.17\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   The ball’s momentum is [latex]\scriptsize 7.17\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the positive direction.
2. [latex]\scriptsize m=58\ \text{g}=0.058\ \text{kg}[/latex]
   [latex]\scriptsize v=246.2\ \text{km/h}=68.39\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   Define the direction in which the ball is served as positive.
   [latex]\scriptsize p=m\cdot v=0.058\ \text{kg}\times 68.39\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}=3.97\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   The ball’s momentum is [latex]\scriptsize 3.97\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the positive direction.
3. The cricket ball bowled by Shoaib Akhtar had more momentum than the tennis ball served by Andy Roddick. Therefore, it would be better to face the serve from Andy Roddick because, if the ball did hit you, it would hurt less.

Back to Exercise 1.1

Exercise 1.2

1. [latex]\scriptsize m=590\ \text{g}=0.590\ \text{kg}[/latex]
   [latex]\scriptsize {{v}_{i}}=7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] towards the ground
   [latex]\scriptsize {{v}_{i}}=4.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] away from the ground
   .
   Define towards the ground as positive.
   [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=0.590\ \text{kg}\times (-4.2\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-7\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-6.61\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   The ball’s change in momentum is [latex]\scriptsize 6.61\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] away from the ground.
2. [latex]\scriptsize m=2.2\ \text{kg}[/latex]
   [latex]\scriptsize \Delta p=-5.73\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   [latex]\scriptsize {{v}_{f}}=13\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
   .
   Define the brick’s direction towards and through the glass as positive. Note that the change in momentum is negative. The brick will travel more slowly after hitting the glass. Therefore, its momentum will be less. Because it will still be travelling in the same (positive) direction, this change (or loss) of momentum will be negative.
   [latex]\scriptsize \begin{align*}\Delta p & =m({{v}_{f}}-{{v}_{i}})\\\therefore {{v}_{f}}-{{v}_{i}} & =\displaystyle \frac{{\Delta p}}{m}\\\therefore {{v}_{i}} & ={{v}_{f}}-\displaystyle \frac{{\Delta p}}{m}\\ & =13\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-\displaystyle \frac{{(-5.73\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}})}}{{2.2\ \text{kg}}}\\ & =15.60\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
   .
   The brick’s velocity just before hitting the glass was [latex]\scriptsize 15.60\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the positive direction.

Back to Exercise 1.2

Exercise 1.3

1. .
   1. Car A:
      [latex]\scriptsize m=1.3\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] clockwise
      [latex]\scriptsize {{v}_{f}}=1.6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] clockwise
      .
      Define clockwise as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=1.3\ \text{kg}\times (1.6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-12\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The change in momentum of car A is [latex]\scriptsize 13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the anti-clockwise direction.
      .
      Car B:
      [latex]\scriptsize m=1.12\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=1.04\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] anti-clockwise
      [latex]\scriptsize {{v}_{f}}=11.03\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]m.s-1 clockwise
      .
      Define clockwise as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=1.12\ \text{kg}\times \left( {11.03\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-(-1.04)\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)=13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The change in momentum of car B is [latex]\scriptsize 13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]in the clockwise direction.
   2. [latex]\scriptsize \text{impulse}=\Delta p[/latex]
      [latex]\scriptsize \text{impuls}{{\text{e}}_{{\text{Car A}}}}=-13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] or [latex]\scriptsize 13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the anti-clockwise direction
      [latex]\scriptsize \text{impuls}{{\text{e}}_{{\text{Car B}}}}=13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] or [latex]\scriptsize 13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the clockwise direction
   3. As the magnitude of the change in momentum is the same for both cars, we can use the change in momentum for either car in the calculation. We are calculating time and so direction is not required.
      [latex]\scriptsize \begin{align*}{{F}_{{nett}}}&=16.2\ \text{N}\\\Delta p&=13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
      .
      [latex]\scriptsize \begin{align*}\text{impulse}&={{F}_{{nett}}}\cdot \Delta t\\\therefore \Delta t&=\displaystyle \frac{{\Delta p}}{{{{F}_{{nett}}}}}=\displaystyle \frac{{13.52\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{16.2\ \text{N}}}=0.83\ \text{s}\end{align*}[/latex]
      .
      The duration of the collision was [latex]\scriptsize 0.83\ \text{s}[/latex].
2. .
   1. [latex]\scriptsize m=22\ \text{g}=0.022\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=330\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{f}}=210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      Define the bullet’s direction towards and through the target as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=0.022\ \text{kg}\times (210\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-330\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The change in the momentum of the bullet is [latex]\scriptsize 2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the negative direction.
   2. [latex]\scriptsize \text{impulse}=\Delta p=-2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      Impulse is [latex]\scriptsize 2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the negative direction.
   3. [latex]\scriptsize \Delta t=0.00013\ \text{s}[/latex]
      [latex]\scriptsize \Delta p=-2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      [latex]\scriptsize \begin{align*}\text{impulse}&={{F}_{{nett}}}\cdot \Delta t\\\therefore {{F}_{{nett}}}&=\displaystyle \frac{{\Delta p}}{{\Delta t}}=\displaystyle \frac{{-2.64\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.00013\ \text{s}}}=-20\ 307.70\ \text{N}\end{align*}[/latex]
      .
      The bullet experienced a force of [latex]\scriptsize 20\ 307.70\ \text{N}[/latex] in the opposite direction to its motion.
3. .
   1. [latex]\scriptsize m=400\ \text{g}=0.4\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{f}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      Define towards the wall as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=0.4\ \text{kg}\times (0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-9\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-3.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The impulse of the clay is [latex]\scriptsize 3.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] in the opposite direction to its initial motion.
   2. [latex]\scriptsize \Delta t=0.25\ \text{s}[/latex]
      [latex]\scriptsize \Delta p=-3.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      [latex]\scriptsize \begin{align*}\text{impulse}&={{F}_{{nett}}}\cdot \Delta t\\\therefore {{F}_{{nett}}}&=\displaystyle \frac{{\Delta p}}{{\Delta t}}=\displaystyle \frac{{-3.6\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.25\ \text{s}}}=-14.4\ \text{N}\end{align*}[/latex]
      .
      The force exerted by the wall on the clay is [latex]\scriptsize 14.4\ \text{N}[/latex] in the opposite direction to the clay’s initial motion. Therefore, the force exerted by the clay on the wall is [latex]\scriptsize 14.4\ \text{N}[/latex] in the direction of the clay’s original motion because the force exerted by the wall on the clay will be equal in magnitude but opposite in direction to the force exerted by the clay on the wall.

Back to Exercise 1.3

Unit 1: Assessment

Question 1 adapted from Everything Science Grade 12 Worked example 16 page 55

1. .
   1. [latex]\scriptsize m=156\ \text{g}=0.156\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=54\ \text{km/h}=15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{f}}=-36\ \text{km/h}=-10\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      Define from bowler to batsman as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=0.156\ \text{kg}\times (-10\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-3.9\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The ball’s impulse (or change in momentum) is [latex]\scriptsize 3.9\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] from batsman to bowler.
   2. [latex]\scriptsize \Delta t=0.13\ \text{s}[/latex]
      [latex]\scriptsize \Delta p=-3.9\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      [latex]\scriptsize \begin{align*}\text{impulse}&={{F}_{{nett}}}\cdot \Delta t\\\therefore {{F}_{{nett}}}&=\displaystyle \frac{{\Delta p}}{{\Delta t}}=\displaystyle \frac{{-3.9\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.13\ \text{s}}}=-30\ \text{N}\end{align*}[/latex]
      .
      The average force exerted by the bat is [latex]\scriptsize 30\ \text{N}[/latex] in the direction batsman to bowler.
2. .
   1. [latex]\scriptsize m=24\ \text{g}=0.024\ \text{kg}[/latex]
      [latex]\scriptsize {{v}_{i}}=105\ \text{km/h}=29.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      [latex]\scriptsize {{v}_{f}}=-43\ \text{km/h}=-11.94\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      Define from racquet towards player who gets hit as positive.
      [latex]\scriptsize \Delta p=m({{v}_{f}}-{{v}_{i}})=0.024\ \text{kg}\times (-11.94\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-29.17\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}})=-0.99\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      The change in the ball’s momentum is [latex]\scriptsize 0.99\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] from the hit player to the racquet.
   2. [latex]\scriptsize \text{impulse}=\Delta p=-0.99\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]in the direction from the hit player to the racquet.
   3. [latex]\scriptsize \Delta t=0.017\ \text{s}[/latex]
      [latex]\scriptsize \Delta p=-0.99\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
      .
      [latex]\scriptsize \begin{align*}\text{impulse}&={{F}_{{nett}}}\cdot \Delta t\\\therefore {{F}_{{nett}}}&=\displaystyle \frac{{\Delta p}}{{\Delta t}}=\displaystyle \frac{{-0.99\ \text{kg}\text{.m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.017\ \text{s}}}=-58.24\ \text{N}\end{align*}[/latex]
      .
      The force exerted by the player’s leg on the ball is [latex]\scriptsize 58.24\ \text{N}[/latex] in the opposite direction to the ball’s initial motion. Therefore, the force exerted by the ball on the player’s leg is [latex]\scriptsize 58.24\ \text{N}[/latex] in the direction of the ball’s original motion (from racquet to hit player) because the force exerted by the leg on the ball will be equal in magnitude but opposite in direction to the force exerted by the ball on the leg.
3. A crumple zone will reduce the impulse during a collision by extending the time over which the vehicle’s velocity reduces and hence the time over which its momentum changes. Because [latex]\scriptsize \text{impulse}=\Delta p={{F}_{{nett}}}\cdot \Delta t[/latex], if [latex]\scriptsize t[/latex] increases for a constant [latex]\scriptsize \Delta p[/latex] then [latex]\scriptsize {{F}_{{nett}}}[/latex] will decrease and less force will be applied to the passengers in the car.

Back to Unit 1: Assessment