Chemical Change: Identify and apply knowledge of acids and bases
Unit 1: Acids and Bases
Emma Harrage
Unit outcomes
By the end of this unit you will be able to:
- Identify acids, bases and buffers using definitions of Arrhenius and Lowry Bronsted.
- Apply pH values.
- Write neutralisation (acid-base) reactions down and calculate unknown value.
- Explain the use of indicators and titration.
- Identify industrial acids and alkali and their application.
What you should know
Before you start this unit, make sure you can:
- Balance chemical equations. Refer to level 3 subject outcome 6.2 unit 1 if you need help with this.
- Understand that there are different types of chemical reactions. Refer to level 3 subject outcome 6.3 unit 1 if you need help with this.
Introduction
Parts of the text in this unit were sourced from Siyavula Physical Science Gr 12 Learner’s Book, Chapter 9, released under a CC-BY licence.
In this unit you will learn about acids and bases. An acid is defined as a substance which has [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex] ions and the strength of an acid depends on how many of those ions it has. Strong acids include hydrochloric, nitric, and sulphuric acids which are used in laboratories and industry. Common acids include lemon juice (citric acid), vinegar (acetic acid, also called ethanoic acid), carbonic acid and lactic acid which is in milk. Bases are the chemical opposites of acids. An example of a strong bases is sodium hydroxide, and ammonia is a weak base. Household bases include baking soda, bicarbonate of soda, milk of magnesia, indigestion remedies, borax and most cleaning products including toothpaste and soaps. The pH scale gives a measure of the acidity or alkalinity of a solution and is determined using indicators.
What are acids and bases?
We encounter many examples of acids and bases in our daily lives. Some common examples of household items that contain acids are vinegar (contains acetic acid, also called ethanoic acid), lemon juice (contains citric and ascorbic acid), wine (contains tartaric acid). These acids are often found to have a sour taste. Hydrochloric acid, sulfuric acid and nitric acid are examples of acids that are more likely to be found in laboratories and industry.
Hydrochloric acid is also found in the gastric juices in the stomach. Fizzy (carbonated) drinks contain carbonic acid, while tea and wine contain tannic acid. People even use acids in an artistic process known as acid etching. In acid etching, a metal is covered in a waxy material that is resistant to acid. The bare metal is then exposed in the desired pattern and the sample is placed in an acid bath.
Bases that you may know about include sodium hydroxide (commonly known as caustic soda), ammonium hydroxide and ammonia. Some of these are found in household cleaning products. Bases are usually found to have a bitter taste and feel slippery (soap is a good example). Acids and bases are also important commercial components in the fertiliser, plastics, and petroleum-refining industries.
| Acid | Formula | Base | Formula |
| Hydrochloric acid | [latex]\scriptsize \displaystyle \text{HCl}[/latex] | Sodium hydroxide | [latex]\scriptsize \displaystyle \text{NaOH}[/latex] |
| Sulfuric acid | [latex]\scriptsize \displaystyle {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex] | Potassium hydroxide | [latex]\scriptsize \displaystyle \text{KOH}[/latex] |
| Nitric acid | [latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{3}}[/latex] | Magnesium hydroxide | [latex]\scriptsize \displaystyle \text{Mg}{{{\left( {\text{OH}} \right)}}_{2}}[/latex] |
| Oxalic acid | [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{C}}_{\text{2}}}{{\text{O}}_{\text{4}}}[/latex] | Calcium hydroxide | [latex]\scriptsize \displaystyle \text{Ca}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] |
| Sulfurous acid | [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{3}}}[/latex] | Sodium bicarbonate | [latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex] |
| Phosphoric acid | [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}\text{P}{{\text{O}}_{\text{4}}}[/latex] | Sodium carbonate | [latex]\scriptsize \displaystyle \text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}[/latex] |
| Acetic (ethanoic) acid | [latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{\text{3}}}\text{COOH}[/latex] | Ammonium hydroxide | [latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{4}}}\text{OH}[/latex] |
| Carbonic acid | [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}[/latex] | Ammonia | [latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{3}}[/latex] |
Models for acids and bases
For the acids you will encounter, an acid is a molecule that donates a [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex] ion.
Substances that will act as a base include hydroxides, oxides, carbonates, or hydrogen carbonates, among others. Bases often release free hydroxide ions ([latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex]) when dissociating in water.
Arrhenius model for acids and bases
A few models for acids and bases have been developed over the years. One of the earliest was the Arrhenius definition. In 1884, Arrhenius discovered that water dissociates (splits up) into hydronium ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex]) and hydroxide ([latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex]) ions according to the following equation:
[latex]\scriptsize \displaystyle \text{2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\rightleftharpoons {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{+O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
Another way of writing this is:
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\rightleftharpoons {{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{+O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
Arrhenius described an acid as a compound that forms [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex] when added to water. An Arrhenius acid therefore increases the concentration of [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex] ions in water. Arrhenius described a base as a compound that dissociates in water to form [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions. An Arrhenius base therefore increases the concentration of [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions in water.
Take note!
The definition of Arrhenius acids and bases: An Arrhenius acid forms [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex] in water (increases [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex]). An Arrhenius base forms[latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] in water (increases [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex]).
Look at the following examples showing the dissociation of hydrochloric acid and sodium hydroxide:
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{ + }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{ }\to {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}_{{\left( {\text{aq}} \right)\text{ }}}\text{+ C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
Hydrochloric acid in water increases the concentration of [latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex] ions and is therefore an acid.
Sodium hydroxide in water increases the concentration of [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions and is therefore a base:
[latex]\scriptsize \displaystyle ~\text{NaO}{{\text{H}}_{{\left( \text{s} \right)}}}\text{ + }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{ }\to \text{ N}{{\text{a}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{ + O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{ + }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
However, this definition can only be used for acids and bases in water. Since there are many reactions which do not occur in water, it was important to come up with a much broader definition for acids and bases.
Brønsted-Lowry model for acids and bases
In 1923, Lowry and Brønsted took the work of Arrhenius further to develop a broader definition for acids and bases. The Brønsted-Lowry model defines acids and bases in terms of their ability to donate or accept protons.
Hydrogen atoms contain only one proton and one electron. [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex] is a hydrogen atom that has lost its electron and is often called a proton.
Take note!
The definition of Brønsted-Lowry acids and bases: An acid is a substance that donates (gives away) protons ([latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex]). A base is a substance that accepts (takes) protons.
Under the Brønsted-Lowry definition an acid is a proton donor because it donates [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex] and a base is a proton acceptor because it accepts [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex].
Below are some examples:
- [latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ N}{{\text{H}}_{{\text{3}\left( \text{g} \right)\text{ }}}}\to \text{ N}{{\text{H}}^{{\text{+4}}}}_{{\left( {\text{aq}} \right)}}\text{+ C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
To decide which substance is a proton donor and which is a proton acceptor, we need to look at what happens to each reactant. The reaction can be broken down as follows:
.
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{ }\to {{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{ + C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
HCl donates a proton. It is a proton donor and is therefore the acid.
.
[latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{{\text{3}\left( \text{g} \right)}}}\text{ + }{{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\to \text{N}{{\text{H}}^{{\text{+4}}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
[latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{3}}}[/latex]accepts a proton. It is a proton acceptor and is therefore the base. - [latex]\scriptsize \displaystyle ~\text{C}{{\text{H}}_{\text{3}}}\text{COO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\to {{\text{H}}_{3}}{{\text{O}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{+ C}{{\text{H}}_{\text{3}}}\text{CO}{{\text{O}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
The reaction can be broken down as follows:
.
[latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{\text{3}}}\text{COO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\text{ }\to \text{ C}{{\text{H}}_{\text{3}}}\text{CO}{{\text{O}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{ + }{{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
[latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{\text{3}}}\text{COOH}[/latex]donates a proton. It is a proton donor and is therefore the acid.
.
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{ + }{{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\to {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
Water accepts a proton. It is a proton acceptor and is therefore the base. - [latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{{\text{3}\left( \text{g} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{ }\to \text{N}{{\text{H}}^{\text{4}}}{{^{+}}_{{\left( {\text{aq}} \right)}}}\text{+ O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
The reaction can be broken down as follows:
.
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{ }\to \text{ O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{ + }{{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
Water donates a proton. It is a proton donor and is therefore the acid.
.
[latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{{\text{3}\left( \text{g} \right)}}}\text{ + }{{\text{H}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\to \text{N}{{\text{H}}^{{\text{4+}}}}_{{\left( {\text{aq}} \right)}}[/latex]
.
Ammonia accepts a proton. It is a proton acceptor and is therefore the base.
Notice that in example 2 water acted as a base, while in example 3 water acted as an acid. Water can act as both an acid and a base depending on the reaction. A substance that can act as either an acid or a base is called or .
An amphiprotic substance can donate a proton in one reaction (a Brønsted-Lowry acid) or accept a proton in another reaction (a Brønsted-Lowry base).
Substances such as ammonia ([latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{3}}}[/latex]), zinc oxide ([latex]\scriptsize \displaystyle \text{ZnO}[/latex]), and beryllium hydroxide ([latex]\scriptsize \displaystyle \text{Be}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex]) are amphoteric. Water and is also amphiprotic.
Weak acids and bases
A weak acid or base is one where only a small percentage of molecules will dissociate to form ions in solution.
Take note!
A weak acid or base is defined as substance one where only a small percentage of molecules dissociate to form ions in solution.
Hydrogen fluoride ([latex]\scriptsize \displaystyle \text{HF}[/latex]) is an example of a weak acid. For example if [latex]\scriptsize \displaystyle 100\text{ }000[/latex] molecules of [latex]\scriptsize \displaystyle \text{HF}[/latex] are added to water and only [latex]\scriptsize \displaystyle 100[/latex] ionise to form [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex] and [latex]\scriptsize \displaystyle {{\text{F}}^{\text{-}}}[/latex] ions, then there is only a small amount of ionisation. This is what makes [latex]\scriptsize \displaystyle \text{HF}[/latex] a weak acid.
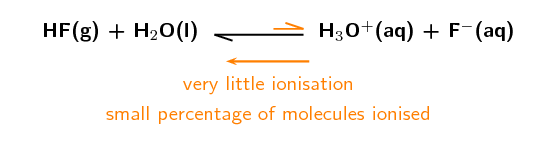
An example of a weak base is magnesium hydroxide ([latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex]), which will only dissociate partially into [latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex] and [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions.
Dilute and concentrated solutions
A different concept to strong and weak is the concept of concentrated and dilute. Where strong and weak refer to the characteristic of a compound, concentrated and dilute refer to the characteristic of a solution. Thus a strong acid can be prepared as either a or a . A solution of which the exact concentration is known is called a .
- A standard solution is one where the exact concentration of solute in a solvent is known.
- A concentrated solution is one where a large amount of a substance (solute) has been added to a solvent. Note that both strong and weak acids and bases can be used in concentrated solutions.
- A dilute solution is one where a small amount of a substance has been added to a solvent. Note that both strong and weak acids and bases can be used in dilute solutions.
A concentrated solution can be made from a strong or a weak acid or base. A dilute solution can also be made from a strong or a weak acid or base. Whether a solution is concentrated or dilute depends on how much of the acid or base was added to the solvent.
A strong base that is also concentrated would be a base that almost completely dissociates when added to a solution, and you also add a large amount of the base to the solution.
A weak acid that is also dilute would be an acid where only a small percentage of molecules ionise when added to a solution, and you also add only a small amount of the acid to the solution.
| Acid | Base | |
| Strong | high percentage forms ions in solution | high percentage forms ions in solution |
| Weak | only a small percentage forms ions in solution | only a small percentage forms ions in solution |
| Concentrated | large number of moles of acid in solution | large number of moles of base in solution |
| Dilute | small number of moles of acid in solution | small number of moles of base in solution |
There are only six strong inorganic acids, the rest are considered weak. These are:
- [latex]\scriptsize \displaystyle \text{HCl}{{\text{O}}_{\text{4}}}[/latex] (perchloric acid)
- [latex]\scriptsize \displaystyle \text{HI}[/latex](hydroiodic acid)
- [latex]\scriptsize \displaystyle \text{HBr}[/latex](hydrobromic acid)
- [latex]\scriptsize \displaystyle \text{HCl}[/latex](hydrochloric acid)
- [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex](sulfuric acid)
- [latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{\text{3}}}[/latex](nitric acid).
Example 1.1
Solution 1 contains [latex]\scriptsize \displaystyle 100\text{ d}{{\text{m}}^{\text{3}}}[/latex] of HCl added to [latex]\scriptsize \displaystyle 10\text{ d}{{\text{m}}^{\text{3}}}[/latex] of water. Almost all the HCl molecules ionise in the solution.
Solution 2 contains [latex]\scriptsize \displaystyle 0.01\text{ g}[/latex] of [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] added to [latex]\scriptsize \displaystyle \text{1 000 d}{{\text{m}}^{\text{3}}}[/latex] of water. Only a small percentage of the [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] molecules dissociate in the solution.
Say whether these solutions:
- Contain a strong or weak acid or base.
- Are concentrated or dilute.
- Are the compounds acids or bases?
Solution
HCl is hydrochloric acid. It would donate a proton and is an acid.
[latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] is magnesium hydroxide and is a base.
Step1: What makes an acid or base strong or weak?
Almost complete ionisation or dissociation means an acid or base is strong. Only a small amount of ionisation or dissociation means an acid or base is weak.
Step 2: What makes a solution concentrated or dilute?
A concentrated solution has a high ratio of solute to solvent. A dilute solution has a low ratio of solute to solvent.
Are the solutions concentrated or dilute?
[latex]\scriptsize \displaystyle 100\text{ d}{{\text{m}}^{\text{3}}}[/latex] of HCl is added to [latex]\scriptsize \displaystyle 10\text{ d}{{\text{m}}^{\text{3}}}[/latex] of water. This is a high ratio, therefore the solution of HCl is concentrated.
[latex]\scriptsize \displaystyle 0.01\text{ g}[/latex] of [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] is added to [latex]\scriptsize \displaystyle \text{1 000 d}{{\text{m}}^{\text{3}}}[/latex] of water. This is a low ratio, therefore the solution of [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] is dilute.
Step 3: Are the compounds strong or weak acids and bases?
Almost all the HCl molecules ionise in the solution, therefore HCl is a strong acid.
Only a small percentage of the [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] molecules dissociate, therefore [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex] is a weak base.
Step 4: Combine your information
Solution 1 is a concentrated solution of a strong acid.
Solution 2 is a dilute solution of a weak base.
To calculate the concentration of a solution we use the formula: [latex]\scriptsize \displaystyle c\text{ }\left( {\text{mol}\text{.d}{{\text{m}}^{{\text{-3}}}}} \right)=\displaystyle \frac{{n\text{ }\left( {\text{mol}} \right)}}{{V\text{ }\left( {\text{d}{{\text{m}}^{\text{3}}}} \right)}}[/latex]
Example 1.2
[latex]\scriptsize \displaystyle 0.27\text{ g}[/latex] of [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] is added to [latex]\scriptsize \displaystyle 183.7\text{ d}{{\text{m}}^{\text{3}}}[/latex] of water. Calculate the concentration of the solution.
Solution
Step 1: List the information you have and the information you need
V =[latex]\scriptsize \displaystyle 183.7\text{ d}{{\text{m}}^{\text{3}}}[/latex], m = [latex]\scriptsize \displaystyle 0.27\text{ g}[/latex]
The volume (V) and the mass (m) are given. The number of moles (n) needs to be calculated. To do that the molar mass (M) needs to be calculated.
Step 2: Make sure all given units are correct and convert them if necessary
All the units are correct.
Step 3: What equations will be necessary to calculate the concentration?
[latex]\scriptsize \displaystyle c\left( {\text{mol}\text{.d}{{\text{m}}^{{\text{-3}}}}} \right)=\displaystyle \frac{{n\text{ }\left( {\text{mol}} \right)}}{{V\text{ }\left( {\text{d}{{\text{m}}^{\text{3}}}} \right)}}[/latex]
[latex]\scriptsize \displaystyle n\text{ }\left( {\text{mol}} \right)=\displaystyle \frac{{m\text{ }\left( \text{g} \right)}}{{M\text{ }\left( {\text{g}\text{.mo}{{\text{l}}^{{\text{-1}}}}} \right)}}[/latex]
Step 4: Calculate the number of moles of the acid in the solution
[latex]\scriptsize \displaystyle \begin{align*}{M}_{\left( {{H}_{2}}S{{O}_{4}} \right)}&=\left( {2\text{ x }1.01} \right)+32.1+\left( {4\text{ x}16} \right)=98.12\text{ g}\text{.mo}{\text{l}}^{{\text{-1}}}\\ n=\displaystyle \frac{m}{M}&=\displaystyle \frac{{0.27}}{{98.12}}\text{= }0.0028\text{ mol}\end{align*}[/latex]
Step 5: Calculate the concentration of the solution
[latex]\scriptsize \displaystyle \begin{align*}c&=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.0028\text{ mol}}}{{183.7\text{ d}{{\text{m}}^{\text{3}}}}}\\&=0.0000152\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}=1.52\times {{10}^{{-5}}}\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}\end{align*}[/latex]
Example 1.3
[latex]\scriptsize \displaystyle 16.4 \text{g}[/latex] of KOH is added to [latex]\scriptsize \displaystyle 12.9\text{ c}{{\text{m}}^{\text{3}}}[/latex] of water. Calculate the concentration of the solution.
Solution
Step 1: List the information you have and the information you need
V =[latex]\scriptsize \displaystyle 12.9\text{ c}{{\text{m}}^{\text{3}}}[/latex], m = [latex]\scriptsize \displaystyle 16.4 \text{g}[/latex]
The volume (V) and the mass (m) are given. The number of moles (n) needs to be calculated. To do that the molar mass (M) needs to be calculated.
Step 2: Make sure all given units are correct or convert them
The volume needs to be converted to [latex]\scriptsize \displaystyle \text{d}{{\text{m}}^{\text{3}}}[/latex].
[latex]\scriptsize \displaystyle V\text{ }=\text{ }12.9\text{ c}{{\text{m}}^{\text{3}}}\times \displaystyle \frac{{0.001\text{ d}{{\text{m}}^{\text{3}}}}}{{1\text{ c}{{\text{m}}^{\text{3}}}}}=0.0129\text{ d}{{\text{m}}^{\text{3}}}[/latex]
Step 3: What equations will be necessary to calculate the concentration?
[latex]\scriptsize \displaystyle c\left( {\text{mol}\text{.d}{{\text{m}}^{{\text{-3}}}}} \right)=\displaystyle \frac{{n\text{ }\left( {\text{mol}} \right)}}{{V\text{ }\left( {\text{d}{{\text{m}}^{\text{3}}}} \right)}}[/latex]
[latex]\scriptsize \displaystyle n\text{ }\left( {\text{mol}} \right)=\displaystyle \frac{{m\text{ }\left( \text{g} \right)}}{{M\text{ }\left( {\text{g}\text{.mo}{{\text{l}}^{{\text{-1}}}}} \right)}}[/latex]
Step 4: Calculate the number of moles of base in the solution
[latex]\scriptsize \displaystyle \begin{align*} {{M}_{{\left( {\text{KOH}} \right)}}}&=39.1+16+1.01=56.11\text{ g}\text{.mo}{{\text{l}}^{{\text{-1}}}} \\ n=\displaystyle \frac{m}{M}&=\displaystyle \frac{{16.4\text{ g}}}{{56.11\text{ g}\text{.mo}{{\text{l}}^{{-1}}}}=\text{ }0.292\text{ mol}} \end{align*}[/latex]
Step 5: Calculate the concentration of the solution
[latex]\scriptsize \displaystyle c=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.292\text{ mol}}}{{0.0129\text{ d}{{\text{m}}^{\text{3}}}}}\text{ }=\text{ }22.64\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
Exercise 1.1
- Say whether the solutions of the acids and bases in the following situations are concentrated or dilute.
- For every [latex]\scriptsize \displaystyle 1[/latex] mole of a solvent there are [latex]\scriptsize \displaystyle 50[/latex] moles of lithium hydroxide ([latex]\scriptsize \displaystyle \text{LiOH}[/latex]).
- For every [latex]\scriptsize \displaystyle 100[/latex] moles of a solvent there are [latex]\scriptsize \displaystyle 5[/latex] moles of nitric acid ([latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{\text{3}}}[/latex]).
- Calculate the concentration of the following solutions:
- [latex]\scriptsize \displaystyle 27\text{ g}[/latex] of sodium bicarbonate ([latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex]) added to [latex]\scriptsize \displaystyle 22.6\text{ c}{{\text{m}}^{\text{3}}}[/latex] of water.
- [latex]\scriptsize \displaystyle 0.893\text{ mol}[/latex] of phosphoric acid ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}\text{P}{{\text{O}}_{\text{4}}}[/latex]) added to [latex]\scriptsize \displaystyle 4.79\text{ d}{{\text{m}}^{\text{3}}}[/latex] of a solvent.
The full solutions are at the end of the unit.
Acid-base reactions
When an acid and a base react, they form a . If the base contains hydroxide ([latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{-}}[/latex]) ions, then water will also be formed. The word salt is a general term which applies to the products of all acid-base reactions. A salt is a product that is made up of the cation from a base and the anion from an acid.
A cation is an ion (charged atom or molecule) with a positive (+) charge. An anion is an ion with a negative (-) charge.
Salts are not just the table salt you put on your food. A salt is any compound made up of stoichiometrically equivalent amounts of cations and anions to make a neutral, ionic compound.

When an equivalent amount of acid and base react (so that neither the acid nor the base are in excess), the reaction is said to have reached the . At this point has been achieved.
Look at the following examples:
- Hydrochloric acid with sodium hydroxide:
.
Hydrochloric acid reacts with sodium hydroxide to form sodium chloride (the salt) and water. Sodium chloride is made up of [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{\text{+}}}[/latex] cations from the base ([latex]\scriptsize \displaystyle \text{NaOH}[/latex]) and [latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{\text{-}}}[/latex] anions from the acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]).
.
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex] - Hydrogen bromide with potassium hydroxide:
.
Hydrogen bromide reacts with potassium hydroxide to form potassium bromide (the salt) and water. Potassium bromide is made up of [latex]\scriptsize \displaystyle {{\text{K}}^{\text{+}}}[/latex] cations from the base ([latex]\scriptsize \displaystyle \text{KOH}[/latex]) and [latex]\scriptsize \displaystyle \text{B}{{\text{r}}^{\text{-}}}[/latex] anions from the acid ([latex]\scriptsize \displaystyle \text{HBr}[/latex]).
.
[latex]\scriptsize \displaystyle \text{HB}{{\text{r}}_{{\left( {\text{aq}} \right)}}}\text{+KO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{KB}{{\text{r}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex] - Hydrochloric acid with sodium hydrogen carbonate:
.
Hydrochloric acid reacts with sodium hydrogen carbonate to form sodium chloride (the salt), water and carbon dioxide. Sodium chloride is made up of [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{\text{+}}}[/latex] cations from the base ([latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex]) and [latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{\text{-}}}[/latex] anions from the acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]).
.
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+NaHC}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\to \text{NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
You should notice that in the first two examples, the base contained [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions, and therefore the products were a salt and water. [latex]\scriptsize \displaystyle \text{NaCl}[/latex] (table salt) and [latex]\scriptsize \displaystyle \text{KBr}[/latex] are both salts. In the third example, [latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex] also acts as a base, despite not having [latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex] ions. A salt is still formed as one of the products, but carbon dioxide ([latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex]) is produced as well as water.
Neutralisation reactions are very important in everyday life. Below are some examples:
- Domestic uses: Calcium oxide ([latex]\scriptsize \displaystyle \text{CaO}[/latex]) is used to neutralise acidic soil. Powdered limestone ([latex]\scriptsize \displaystyle \text{CaC}{{\text{O}}_{\text{3}}}[/latex]) can also be used, but its action is much slower and less effective. These substances can also be used on a larger scale in farming and in rivers.
- Biological uses: Hydrochloric acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]) in the stomach plays an important role in helping to digest food. It is important to note that too much acid in the stomach may lead to the formation of ulcers in cases where the stomach lining is damaged (e.g. by an infection). Antacids (which are bases) are taken to neutralise excess stomach acid, to prevent damage to the intestines. Examples of antacids are aluminium hydroxide, magnesium hydroxide (milk of magnesia) and sodium bicarbonate (bicarbonate of soda).
- Industrial uses: Alkaline calcium hydroxide (limewater) is used to absorb harmful acidic [latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}[/latex] gas that is released from power stations and from the burning of fossil fuels.
Take note!
Remember the following general equations for the reactions of acids, which you will have learnt in Grade 9:
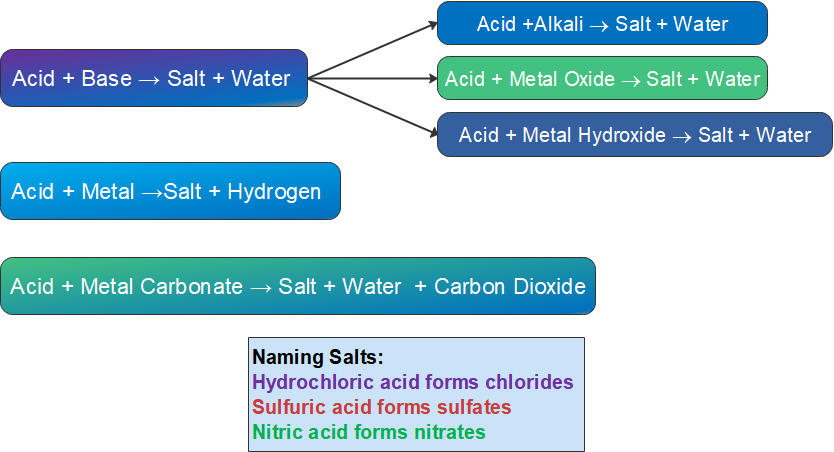
Example 1.4
Determining equations from starting materials:
Magnesium carbonate ([latex]\scriptsize \displaystyle \text{MgC}{{\text{O}}_{\text{3}}}[/latex]) is dissolved in nitric acid ([latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{\text{3}}}[/latex]). Give the balanced chemical equation for this reaction.
Solution
Step 1: What are the reactants?
An acid ([latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{\text{3}}}[/latex]) and a metal carbonate ([latex]\scriptsize \displaystyle \text{MgC}{{\text{O}}_{\text{3}}}[/latex]).
Step 2: What will the products be?
As this is the reaction of an acid and a metal carbonate the products will be a salt, water, and carbon dioxide.
nitric acid + magnesium carbonate → salt + water + carbon dioxide
Step 3: What is the formula of the salt?
The cation will come from the metal carbonate ([latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex]). The anion will come from the acid ([latex]\scriptsize \displaystyle \text{N}{{\text{O}}^{{3-}}}[/latex]). Due to the charges on the cation and anion there must be two [latex]\scriptsize \displaystyle \text{N}{{\text{O}}^{{3-}}}[/latex] for everyone [latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex].
Therefore the formula for the salt will be [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{N}{{\text{O}}_{\text{3}}}} \right)}_{\text{2}}}[/latex].
Step 4: Write the equation for this reaction
[latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\text{+MgC}{{\text{O}}_{{\text{3}\left( \text{s} \right)\text{ }}}}\to \text{ Mg}{{\left( {\text{N}{{\text{O}}_{\text{3}}}} \right)}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
Step 5: Make sure that the equation is balanced
The equation is not balanced.
| Number on left | Number on right | |
| H | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 2[/latex] |
| N | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 2[/latex] |
| O | [latex]\scriptsize 6[/latex] | [latex]\scriptsize 9[/latex] |
| Mg | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
| C | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
To balance this equation there needs to be two nitric acid molecules on the left-hand side.
[latex]\scriptsize \displaystyle \text{2HN}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\text{+MgC}{{\text{O}}_{{\text{3}\left( \text{s} \right)\text{ }}}}\to \text{ Mg}{{\left( {\text{N}{{\text{O}}_{\text{3}}}} \right)}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
| Number on left | Number on right | |
| H | [latex]\scriptsize 2[/latex] | [latex]\scriptsize 2[/latex] |
| N | [latex]\scriptsize 2[/latex] | [latex]\scriptsize 2[/latex] |
| O | [latex]\scriptsize 9[/latex] | [latex]\scriptsize 9[/latex] |
| Mg | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
| C | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
The equation is now balanced.
Example 1.5
Hydroiodic acid ([latex]\scriptsize \displaystyle \text{HI}[/latex]) is added to solid potassium hydroxide ([latex]\scriptsize \displaystyle \text{KOH}[/latex]). Give the balanced chemical equation for this reaction.
Solution
Step 1: What are the reactants?
An acid ([latex]\scriptsize \displaystyle \text{HI}[/latex]) and a base ([latex]\scriptsize \displaystyle \text{KOH}[/latex]).
Step 2: What will the products be?
As this is the reaction of an acid and base (which contains a hydroxide anion) the products will be a salt and water.
hydroiodic acid + potassium hydroxide → salt + water
Step 3: What is the formula of the salt?
The cation will come from the base ([latex]\scriptsize \displaystyle {{\text{K}}^{\text{+}}}[/latex]). The anion will come from the acid ([latex]\scriptsize \displaystyle {{\text{I}}^{\text{-}}}[/latex]). Due to the charges on the cation and anion there must be one [latex]\scriptsize \displaystyle {{\text{K}}^{\text{+}}}[/latex] for everyone [latex]\scriptsize \displaystyle {{\text{I}}^{\text{-}}}[/latex].
Therefore the formula for the salt will be [latex]\scriptsize \displaystyle \text{KI}[/latex].
Step 4: Write the equation for this reaction
[latex]\scriptsize \displaystyle \text{H}{{\text{I}}_{{\left( {\text{aq}} \right)}}}\text{+KO}{{\text{H}}_{{\left( \text{s} \right)}}}\to \text{K}{{\text{I}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
This can also be written: [latex]\scriptsize \displaystyle \text{H}{{\text{I}}_{{\left( {\text{aq}} \right)}}}\text{+KO}{{\text{H}}_{{\left( \text{s} \right)}}}\to \text{ }{{\text{K}}^{\text{+}}}_{{\left( {\text{aq}} \right)}}\text{+}{{\text{I}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
Step 5: Make sure that the equation is balanced
The equation is balanced.
Example 1.6
Sulfuric acid ([latex]\scriptsize \displaystyle {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex]) and ammonia ([latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{3}}}[/latex]) are combined. Give the balanced chemical equation for this reaction.
Solution
Step 1: What are the reactants?
An acid ([latex]\scriptsize \displaystyle {{\text{H}}_{2}}\text{S}{{\text{O}}_{4}}[/latex]) and a base ([latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{3}}}[/latex]).
Step 2: What will the products be?
As this is the reaction of an acid and a base (with no hydroxide anion), there will be a salt as a product. There may or may not be another product.
sulfuric acid + ammonia → salt (+ maybe another product)
Step 3: What is the formula of the salt?
The cation will come from the base accepting an [latex]\scriptsize {{\text{H}}^{+}}[/latex] ([latex]\scriptsize \displaystyle \text{N}{{\text{H}}^{{\text{+4}}}}[/latex]). The anion will come from the acid ([latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}^{{\text{-4}}}[/latex]). Due to the charges on the cation and anion there must be two [latex]\scriptsize \displaystyle \text{N}{{\text{H}}^{{\text{4+}}}}[/latex] for everyone [latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}^{{\text{4-}}}[/latex].
Therefore the formula for the salt will be [latex]\scriptsize \displaystyle {{\left( {\text{N}{{\text{H}}_{\text{4}}}} \right)}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex].
Step 4: Write the equation for this reaction so far
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+ N}{{\text{H}}_{{\text{3}\left( \text{g} \right)}}}\text{ }\to {{\left( {\text{N}{{\text{H}}_{\text{4}}}} \right)}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{ }\left( {\text{+ maybe another product}} \right)[/latex]
Step 5: Determine if there will be another product
There are no atom types that are not accounted for on both sides of the equation, therefore it is unlikely that there will be another product. If the equation can be balanced, then there is no other product.
Step 6: Make sure that the equation is balanced
The equation is not balanced.
| Number on left | Number on right | |
| H | [latex]\scriptsize 5[/latex] | [latex]\scriptsize 8[/latex] |
| S | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
| O | [latex]\scriptsize 4[/latex] | [latex]\scriptsize 4[/latex] |
| N | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 2[/latex] |
To balance this equation there needs to be two ammonia molecules on the left-hand side.
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+ 2N}{{\text{H}}_{{\text{3}\left( \text{g} \right)}}}\text{ }\to {{\left( {\text{N}{{\text{H}}_{\text{4}}}} \right)}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{ }[/latex]
| Number on left | Number on right | |
| H | [latex]\scriptsize 8[/latex] | [latex]\scriptsize 8[/latex] |
| S | [latex]\scriptsize 1[/latex] | [latex]\scriptsize 1[/latex] |
| O | [latex]\scriptsize 4[/latex] | [latex]\scriptsize 4[/latex] |
| N | [latex]\scriptsize 2[/latex] | [latex]\scriptsize 2[/latex] |
The equation is now balanced.
Exercise 1.2
Write balanced equations for these reactions:
- Hydrochloric acid and calcium
- Hydrochloric acid and magnesium hydroxide
- Sulfuric acid and magnesium oxide
The full solutions are at the end of the unit.
The pH scale
The concentration of specific ions in solution determines whether the solution is acidic or basic. Acids and bases can be described as substances that either increase or decrease the concentration of hydrogen ([latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex]) or hydronium ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex]) ions in a solution. An acid increases the hydrogen ion concentration in a solution, while a base decreases the hydrogen ion concentration.
is used to measure the concentration of [latex]\scriptsize \displaystyle {{\text{H}}^{\text{+}}}[/latex] ions [latex]\scriptsize \displaystyle \left( {\left[ {{{\text{H}}^{\text{+}}}} \right]} \right)[/latex]and therefore, whether a substance is acidic or basic (alkaline). Solutions with a pH of less than seven are acidic, while those with a pH greater than seven are basic (alkaline). The pH scale ranges from [latex]\scriptsize \displaystyle 0[/latex] to [latex]\scriptsize \displaystyle 14[/latex] and a pH of [latex]\scriptsize \displaystyle 7[/latex]is considered neutral.

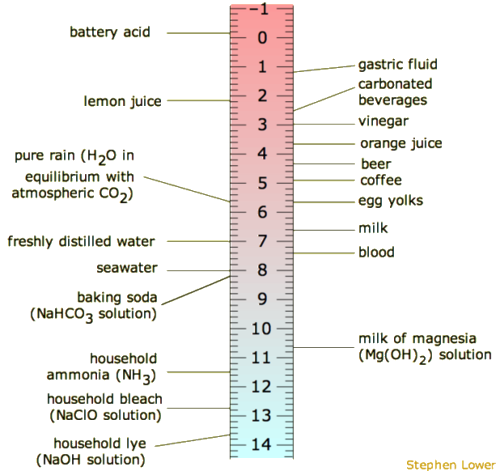
The term pH was first used by in 1909 by Søren Peter Lauritz Sørensen (a Danish biochemist). The p stood for potenz and the H for hydrogen. This translates to power of hydrogen.
| Molecule | Found in | pH | Type |
| Phosphoric acid | Fizzy drinks | [latex]\scriptsize 2.15[/latex] | acid |
| Tartaric acid | Wine | [latex]\scriptsize 2.95[/latex] | acid |
| Citric acid | Lemon juice | [latex]\scriptsize 3.14[/latex] | acid |
| Acetic acid | Vinegar | [latex]\scriptsize 4.76[/latex] | acid |
| Carbonic acid | Fizzy drinks | [latex]\scriptsize 6.37[/latex] | acid |
| Ammonia | Cleaning products | [latex]\scriptsize 11.5[/latex] | base |
| Ammonium hydroxide | Cleaning products | [latex]\scriptsize 11.65[/latex] | base |
| Sodium hydroxide | Caustic soda | [latex]\scriptsize 13[/latex] | base |
A strong acid + strong base form a neutral salt and water solution → pH =[latex]\scriptsize \displaystyle 7[/latex]
For example: [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( \text{l} \right)}}}\text{+NaO}{{\text{H}}_{{\left( \text{s} \right)}}}\to \text{N}{{\text{a}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
A weak acid + strong base form a weak basic salt and water solution → pH = approximately [latex]\scriptsize \displaystyle 9[/latex]
For example: [latex]\scriptsize \displaystyle \text{H}{{\text{F}}_{{\left( \text{l} \right)}}}\text{+NaO}{{\text{H}}_{{\left( \text{s} \right)}}}\to \text{Na}{{\text{F}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
A strong acid + weak base form a weak acidic salt and water solution → pH = approximately [latex]\scriptsize \displaystyle 5[/latex]
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( \text{l} \right)}}}\text{+N}{{\text{H}}_{{\text{3}\left( \text{l} \right)}}}\to {{\left( {\text{N}{{\text{H}}_{\text{4}}}} \right)}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
In agriculture, it is important for farmers to know the pH of their soils so that they can plant the right kinds of crops. The pH of soils can vary depending on several factors, such as rainwater, the kinds of rocks and materials from which the soil was formed and human influences such as pollution and fertilisers. The pH of rainwater can also vary, and this too influences agriculture, buildings, water courses, animals, and plants. Rainwater is naturally acidic because carbon dioxide in the atmosphere combines with water to form carbonic acid. Unpolluted rainwater has a pH of approximately [latex]\scriptsize 4.5[/latex]. However, human activities can alter the acidity of rain, and this can cause serious problems such as acid rain.
Indicators
Indicators are chemical compounds that change colour depending on whether they are in an acidic or a basic solution. Different indicators are used to identify acids and bases. Only a universal indicator can identify an acid and base and give a pH value.

Litmus paper can be used as an acid/base indicator. It is sold in strips. Blue litmus paper will become red in acidic conditions and red litmus paper will become blue in basic conditions. Blue litmus paper is used to detect acidic conditions, while red litmus paper is used to detect basic conditions.

| Preferred indicator | Colour of acid | Colour of base | pH range | |
| strong acid + strong base | bromothymol blue | yellow | blue | [latex]\scriptsize 6.0-7[/latex] |
| weak acid + strong base | phenolphthalein | colourless | pink | [latex]\scriptsize 8.3-10[/latex] |
| strong acid + weak base | bromocresol green | yellow | blue | [latex]\scriptsize \displaystyle 3.8~-~5.4[/latex] |
Titrations
The neutralisation reaction between an acid and a base can be very useful. If an acidic solution of known concentration (a standard solution) is added to a basic (alkaline) solution of unknown concentration until the solution is exactly neutralised (i.e. there is only salt and water), it is possible to calculate the exact concentration of the unknown solution. It is possible to do this because, at the exact point where the solution is neutralised, stoichiometrically equivalent mole amounts of acid and base have reacted with each other.
In a , a known volume of a standard solution (A) is added to a known volume of a solution with unknown concentration (B). The concentration of B can then be determined.
Acids and bases are commonly used in titrations, and the point of neutralisation is called the endpoint of the reaction. If you have an indicator that changes colour in the range of the endpoint pH, then you will be able to see when the endpoint has occurred. Another name for a titration is volumetric analysis.
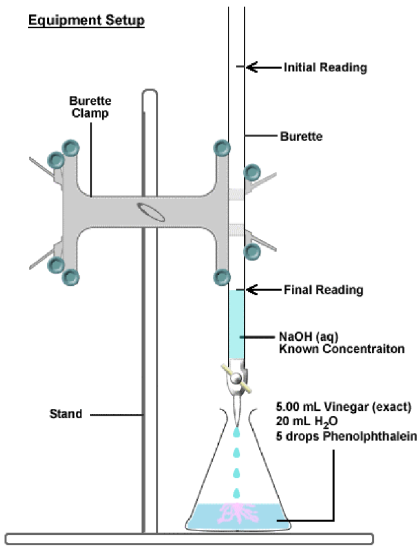
Note
To see an actual titration, watch this video by Fuse Schools, called How to do titrations.
Titration calculations
So how exactly can a titration be carried out to determine an unknown concentration? Look at the following steps to help you to understand the process.
- A carefully measured volume of the solution with unknown concentration is put into a conical flask.
- A few drops of a suitable indicator is added to this solution (bromothymol blue and phenolphthalein are common indicators, refer to table 4).
- The conical flask is placed on a white tile or piece of paper (to make colour changes easier to see).
- A volume of the standard solution (known concentration) is put into a burette (a measuring device) and is slowly added to the solution in the flask, drop by drop.
- At some point, adding one more drop will change the colour of the unknown solution to the colour of the endpoint of the reaction.
- Record the volume of standard solution that has been added up to this point.
- Use the information you have gathered to calculate the exact concentration of the unknown solution. Worked examples are given to walk you through this step.
- Note that adding more solution once the endpoint has been reached will result in a colour change from the endpoint colour to that of the acid (if the solution in the conical flask is a base) or of the base (if the solution in the conical flask is an acid).
When you are busy with these calculations, you will need to remember the following:
- [latex]\scriptsize \displaystyle \text{1 d}{{\text{m}}^{\text{3}}}\text{ = 1 L = 1 000 mL = 1 000 c}{{\text{m}}^{\text{3}}}[/latex], therefore dividing [latex]\scriptsize \displaystyle \text{c}{{\text{m}}^{\text{3}}}[/latex] by [latex]\scriptsize \displaystyle 1\text{ }000[/latex] will give you an answer in [latex]\scriptsize \displaystyle \text{d}{{\text{m}}^{\text{3}}}[/latex]
- the concentration of a solution is measured in [latex]\scriptsize \displaystyle \text{mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
- make sure all the units are correct in your calculations.
Example 1.7
Given the equation: [latex]\scriptsize \displaystyle \text{NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\text{+HC}{{\text{l}}_{{\left( {\text{aq}} \right)\text{ }}}}\to \text{NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
[latex]\scriptsize \displaystyle \text{25 c}{{\text{m}}^{\text{3}}}[/latex] of sodium hydroxide solution was pipetted into a conical flask and titrated with [latex]\scriptsize \displaystyle \text{0}\text{.2 mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex] hydrochloric acid. Using a suitable indicator, it was found that [latex]\scriptsize \displaystyle \text{15 c}{{\text{m}}^{\text{3}}}[/latex] of acid was needed to neutralise the base. Calculate the concentration of the sodium hydroxide.
Solution
Step 1: Make sure that the equation is balanced
There are equal numbers of each type of atom on each side of the equation, so the equation is balanced.
Step 2: Write down all the information you know about the reaction, converting to the correct units
[latex]\scriptsize \begin{align*} \text{NaOH: }V&=\text{25 c}{{\text{m}}^{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{0}\text{.001 d}{{\text{m}}^{\text{3}}}}}{{\text{1 c}{{\text{m}}^{\text{3}}}}}\text{ = 0}\text{.025 d}{{\text{m}}^{\text{3}}}\\ \text{HCl: }V&=\text{15 c}{{\text{m}}^{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{0}\text{.001 d}{{\text{m}}^{\text{3}}}}}{{\text{1 c}{{\text{m}}^{\text{3}}}}}\text{ = 0}\text{.015 d}{{\text{m}}^{\text{3}}}\\ C&=\text{0}\text{.2 mol}\text{.d}{{\text{m}}^{{\text{-3}}}}\end{align*}[/latex]
Step 3: Calculate the number of moles of HCl that are added
[latex]\scriptsize \displaystyle c=\displaystyle \frac{n}{V}[/latex]
Therefore, [latex]\scriptsize \displaystyle {{n}_{{\left( {\text{HCl}} \right)}}}=c\text{ }\times \text{ }V[/latex]
[latex]\scriptsize \displaystyle {{n}_{{\left( {HCl} \right)}}}\text{= }0.2\text{ mol}\text{.d}{{\text{m}}^{{-3}}}\text{ }\times \text{ }0.015\text{ d}{{\text{m}}^{3}}=0.003\text{ mol}[/latex]
[latex]\scriptsize \displaystyle 0.003\text{ moles}[/latex] of [latex]\scriptsize \displaystyle \text{HCl}[/latex] are required to neutralise the base.
Step 4: Calculate the number of moles of sodium hydroxide in the reaction
Look at the equation for the reaction: the molar ratio of [latex]\scriptsize \displaystyle \text{HCl:NaOH is 1:1}\text{.}[/latex]
So for every mole of [latex]\scriptsize \displaystyle \text{HCl}[/latex] , there is one mole of [latex]\scriptsize \displaystyle \text{NaOH}[/latex] that is involved in the reaction. Therefore, if [latex]\scriptsize \displaystyle 0.003\text{ mol HCl}[/latex] is required to neutralise the solution, [latex]\scriptsize \displaystyle 0.003\text{ mol NaOH}[/latex] must have been present in the sample of the unknown solution.
Calculate the concentration of the sodium hydroxide solution:
[latex]\scriptsize \displaystyle {{c}_{{\left( {NaOH} \right)}}}=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.003}}{{0.025}}=0.12\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
The concentration of the NaOH solution is [latex]\scriptsize \displaystyle 0.12~\text{mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
Example 1.8
[latex]\scriptsize \displaystyle 10\text{ g}[/latex] of solid sodium hydroxide is dissolved in [latex]\scriptsize \displaystyle 500\text{ c}{{\text{m}}^{\text{3}}}[/latex] water. Using titration, it was found that [latex]\scriptsize \displaystyle 20\text{ c}{{\text{m}}^{\text{3}}}[/latex] of this solution was able to completely neutralise [latex]\scriptsize \displaystyle 10\text{ c}{{\text{m}}^{\text{3}}}[/latex] of a sulfuric acid solution. Calculate the concentration of the sulfuric acid.
Solution
Step 1: Write a balanced equation for the titration reaction
The reactants are sodium hydroxide ([latex]\scriptsize \displaystyle \text{NaOH}[/latex]) and sulfuric acid ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex]). The base has a hydroxide anion ([latex]\scriptsize \displaystyle \text{OH-}[/latex]), therefore the products will be a salt and water.
The cation for the salt ([latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{\text{+}}}[/latex]) will come from the base. The anion for the salt ([latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}^{{\text{-4}}}[/latex]) will come from the acid. There must be [latex]\scriptsize \displaystyle 2\text{ N}{{\text{a}}^{\text{+}}}[/latex] cations for everyone [latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}^{{\text{-4}}}[/latex] and the salt will be [latex]\scriptsize \displaystyle \text{N}{{\text{a}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex].
To balance the equation we need to multiply the number of sodium hydroxide molecules and the water molecules by two.
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}_{{\left( {\text{aq}} \right)}}\text{+2NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{ N}{{\text{a}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
Step 2: Calculate the concentration of the sodium hydroxide solution
The total volume that the 10 g was dissolved in must be used to calculate the concentration.
[latex]\scriptsize \begin{align*} V&=500\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}=\text{ }0.5\text{ d}{{\text{m}}^{\text{3}}} \\ {{M}_{{\left( {\text{NaOH}} \right)}}}&=23.0\text{ }+\text{ }16.0\text{ }+\text{ }1.01=40.01\text{ g}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\ {{n}_{{\left( {\text{NaOH}} \right)}}}&=\displaystyle \frac{m}{M}=\displaystyle \frac{{10}}{{40.01}}=0.25\text{ mol}\\ {{C}_{{\left( {\text{NaOH}} \right)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.25}}{{0.5}}\text{ }=0.50\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex]
Step 3: Calculate the number of moles of sodium hydroxide that were used in the neutralisation reaction
Remember that only [latex]\scriptsize \displaystyle 20\text{ c}{{\text{m}}^{\text{3}}}[/latex]of the sodium hydroxide solution is used:
[latex]\scriptsize \begin{align*}V&=20\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}=0.02\text{ d}{{\text{m}}^{\text{3}}}\\ c&=\displaystyle \frac{n}{V}\text{ therefore }n=c\times V\\ n&=0.50\times 0.02=0.01\text{ mol} \end{align*}[/latex]
Step 4: Calculate the number of moles of sulfuric acid that were neutralised
According to the balanced chemical equation, the mole ratio of [latex]\scriptsize \displaystyle \text{NaOH}[/latex] to [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] is [latex]\scriptsize \displaystyle 2:1[/latex]. There are [latex]\scriptsize \displaystyle 2[/latex] moles of [latex]\scriptsize \displaystyle \text{NaOH}[/latex] for every [latex]\scriptsize \displaystyle 1[/latex] mole of [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex].
[latex]\scriptsize \displaystyle {{n}_{{\text{(}{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\text{)}}}}\text{= }\displaystyle \frac{{\text{0}\text{.01}}}{\text{2}}\text{ = 0}\text{.005 mol}[/latex]
Step 5: Calculate the concentration of the sulfuric acid solution
Remember that [latex]\scriptsize \displaystyle 10\text{ c}{{\text{m}}^{\text{3}}}[/latex] of the sulfuric acid solution is neutralised.
[latex]\scriptsize \begin{align*} \displaystyle {V}_{{\text{(}{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\text{)}}}10 \text{cm}^3 \times\displaystyle \frac{{\text{0}\text{.001}}}{\text{1}}&=\text{0}\text{.01 } \text{dm}^3\\ c=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.005}}{{0.01}}&=0.5\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex]
Note
To help you with titration calculations you can watch this video by Fuse Schools, called Titration calculations.
Exercise 1.3
- A learner is asked to prepare a standard solution of the weak acid, oxalic acid ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{C}}_{\text{2}}}{{\text{O}}_{\text{4}}}[/latex]), for use in a titration. The volume of the solution must be [latex]\scriptsize \displaystyle 500\text{ c}{{\text{m}}^{\text{3}}}[/latex] and the concentration must be [latex]\scriptsize \displaystyle 0.2\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex].
Calculate the mass of oxalic acid which the learner must dissolve to make up the required standard solution. - The learner titrates this [latex]\scriptsize \displaystyle 0.2\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex] oxalic acid solution against a solution of sodium hydroxide. He finds that [latex]\scriptsize \displaystyle 40\text{ c}{{\text{m}}^{3}}[/latex] of the oxalic acid solution completely neutralises [latex]\scriptsize \displaystyle 35\text{ c}{{\text{m}}^{\text{3}}}[/latex] of the sodium hydroxide solution.
Calculate the concentration of the sodium hydroxide solution.
The full solutions are at the end of the unit.
Applications of acids and bases
There are a variety of important uses of acids in bases.
The production of chlorine
The chlorine-alkali (chloralkali) industry is an important chemical process to produce chlorine and sodium hydroxide. The most common method involves the electrolysis of a concentrated aqueous solution of sodium chloride ([latex]\scriptsize \displaystyle \text{NaCl}[/latex]), which is known as brine.
The chemical reactions that take place in this process are:
[latex]\scriptsize \displaystyle \begin{align*}\text{2C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}&\to \text{C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+2}{{\text{e}}^{\text{-}}}\\ \text{2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+2}{{\text{e}}^{\text{-}}}\text{ }&\to {{\text{H}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 2O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}} \end{align*}[/latex]
There are also [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{+}}[/latex] ions from the [latex]\scriptsize \displaystyle \text{NaCl}[/latex] in the solution. If the products are kept separate (to prevent a reaction between the chlorine and hydroxide) the [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{+}}[/latex] will react with the hydroxide ions making the overall reaction as follows:[latex]\scriptsize \displaystyle \text{2NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ 2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)\text{ }}}}\to \text{C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+ }{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 2NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}[/latex]
The uses of chlorine include:
- the purification of water
- as a disinfectant
- in the production of:
- hypochlorous acid (used to kill bacteria in drinking water), chloroform, carbon tetrachloride
- paper, food
- antiseptics, insecticides, medicines, textiles
- paints, petroleum products, solvents, plastics (such as polyvinyl chloride).
The uses of sodium hydroxide include:
- making soap and other cleaning agents
- purification of bauxite (the ore of aluminium)
- making paper
- making rayon (artificial silk).
If the chlorine and hydroxide ions are not kept separate (i.e. are allowed to react), and the temperature is kept below , then the following occurs:
[latex]\scriptsize \displaystyle \text{C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 2O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\to \text{C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{+ Cl}{{\text{O}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
The balanced chemical equation with the inclusion of the [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{\text{+}}}[/latex] ions is:
[latex]\scriptsize \displaystyle \text{C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 2NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ NaCl}{{\text{O}}_{{\left( {\text{aq}} \right)\text{+}}}}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
The uses of NaClO (sodium hypochlorite) include:
- use in bleaches, disinfectants, and water treatments
- use during root canal surgery and to neutralise nerve agents.
If the temperature is above and mixing occurs, then:
[latex]\scriptsize \displaystyle \text{3C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 6O}{{\text{H}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\to \text{5C}{{\text{l}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{+ Cl}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\text{+3}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
And the balanced chemical equation including [latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{+}}[/latex] ions is:
[latex]\scriptsize \displaystyle \text{3C}{{\text{l}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 6NaO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{5NaC}{{\text{l}}_{{\left( {\text{aq}} \right)\text{ }}}}\text{+ NaCl}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\text{+ 3}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
The uses of [latex]\scriptsize \displaystyle \text{NaCl}{{\text{O}}_{\text{3}}}[/latex] (sodium chlorate) include:
- making chlorine dioxide
- a herbicide
- generating oxygen in chemical oxygen generators.
If calcium chloride was used instead of sodium chloride, then the products would be calcium chloride, calcium hypochlorite and calcium chlorate. Similarly, if potassium chloride was used, the products would be potassium chloride, potassium hypochlorite and potassium chlorate.
The chemistry of hair and hair products
Hair is primarily made up of a protein called keratin. Keratin is a macromolecule and consists largely of the amino acid cystine (an organic acid). Proteins give hair a natural acidic pH of between 4 and 5. The following hair products alter this pH and do controlled damage to get the desired effect.
- Permanent waving application: Another name for a permanent waving application is a perm. Ammonium thioglycolate is also known as a perm salt. The reversible reaction of ammonium thioglycolate (reactant) to form thioglycolic acid and free ammonia (product) is given below:
[latex]\scriptsize \displaystyle \text{HSCH2CO}{{\text{O}}^{\text{-}}}_{{\left( {\text{aq}} \right)}}\text{+N}{{\text{H}}^{\text{+}}}_{{\text{4}\left( {\text{aq}} \right)}}\rightleftharpoons \text{HSC}{{\text{H}}_{\text{2}}}\text{COO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\text{+N}{{\text{H}}_{{\text{3}\left( {\text{aq}} \right)}}}[/latex] - Hair relaxers: Hair relaxers work by doing controlled damage to your hair in much the same way as perms do. They reduce the cystine to cysteine and allow the hair structure to be changed.
.
There are two main types of hair relaxers: lye and no-lye. The lye hair relaxers contain sodium hydroxide ([latex]\scriptsize \displaystyle \text{NaOH}[/latex]) and have a very high pH (in the range [latex]\scriptsize \displaystyle 12-14[/latex]). These types of hair relaxers break bonds and strip the hair of its natural oils. Often heating is also used, and this damages the hair even more.
.
Due to increasing worry about the damage caused by lye hair relaxers, companies have produced no-lye hair relaxers. These still contain basic compounds and are still caustic, but their pH is not as high (pH in the range [latex]\scriptsize \displaystyle 9-11[/latex]).
Summary
In this unit you have learnt the following:
- The Arrhenius definition of acids and bases defines an acid as a substance that increases the concentration of hydronium ions ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{3}}}{{\text{O}}^{\text{+}}}[/latex]) in a solution. A base is defined as a substance that increases the concentration of hydroxide ions ([latex]\scriptsize \displaystyle \text{O}{{\text{H}}^{\text{-}}}[/latex]) in a solution. However, this definition only applies to aqueous solutions (in water).
- The Brønsted-Lowry definition is much broader. An acid is a substance that donates protons ([latex]\scriptsize \displaystyle \text{H}{{\text{ }\!\!~\!\!\text{ }}^{\text{+}}}[/latex]), and a base is a substance that accepts protons.
- In different reactions, certain substances can act as both an acid and a base. These substances are amphoteric substances. Amphiprotic substances are amphoteric substances that are Brønsted-Lowry acids and bases. Water is both amphoteric and amphiprotic.
- A large percentage of molecules in a strong acid or base dissociate or ionise to form ions in solution.
- Only a small percentage of molecules in a weak acid or base dissociate or ionise to form ions in solution.
- In a concentrated solution there is a high ratio of dissolved substance to solvent.
- In a dilute solution there is a low ratio of dissolved substance to solvent.
- When an acid and a base react, they form a salt and water. The salt is made up of a cation from the base and an anion from the acid. An example of a salt is sodium chloride (NaCl), which is the product of the reaction between sodium hydroxide (NaOH) and hydrochloric acid (HCl).
- The reaction between an acid and a base is a neutralisation reaction.
- In the reaction between an acid and a metal the products are a salt and hydrogen.
- In the reaction between an acid and a metal hydroxide or metal oxide the products are a salt and water.
- In the reaction between an acid and a metal carbonate or metal hydrogen carbonate the products are a salt, water, and carbon dioxide.
- The pH scale is a measure of the acidity or alkalinity of a solution. It ranges from 0 to 14. Values greater than 7 indicate a base, while those less than 7 indicate an acid.
- An indicator is a compound that is a different colour in a basic solution, an acidic solution, and at the endpoint of a reaction. They are used to determine the endpoint during a neutralisation reaction.
- Titration is the method used to determine the concentration of a known substance using another, standard, solution. Acid-base titrations are an example.
- Two notable applications of acids and bases are in the chloralkali industry, and in hair products including permanent waving applications, hair relaxers, and hair dyes.
Unit 1: Assessment
Suggested time to complete: 30 minutes
- Calculate the concentration of the following solutions:
- [latex]\scriptsize \displaystyle 32.8\text{ mg}[/latex] of hydrochloric acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]) added to [latex]\scriptsize \displaystyle 12.76\text{ c}{{\text{m}}^{\text{3}}}[/latex] of water
- [latex]\scriptsize \displaystyle 1.12~\text{d}{{\text{m}}^{\text{3}}}[/latex] of a [latex]\scriptsize \displaystyle \text{6}\text{.54 mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex] concentration solution of ammonia ([latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{3}}}[/latex]) added to [latex]\scriptsize \displaystyle 0.50\text{ d}{{\text{m}}^{\text{3}}}[/latex]of water.
- [latex]\scriptsize \displaystyle 25.0\text{ c}{{\text{m}}^{\text{3}}}[/latex] of a [latex]\scriptsize \displaystyle 0.1\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex] standard solution of sodium carbonate was used to neutralise [latex]\scriptsize \displaystyle 35.0\text{ c}{{\text{m}}^{\text{3}}}[/latex] of a solution of hydrochloric acid.
- Write a balanced chemical equation for the reaction.
- Calculate the concentration of the acid.
- The stomach secretes gastric juice, which contains hydrochloric acid. The gastric juice helps with digestion. Sometimes there is an overproduction of acid, leading to heartburn or indigestion. Antacids, such as milk of magnesia, can be taken to neutralise the excess acid. Milk of magnesia is only slightly soluble in water and has the chemical formula [latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex].
- Write a balanced chemical equation to show how the antacid reacts with the acid.
- The instructions on the bottle recommend that children under the age of [latex]\scriptsize \displaystyle 12[/latex] years take one teaspoon of milk of magnesia, whereas adults can take two teaspoons of the antacid. Briefly explain why the dosages are different.
- Why is it not advisable to take an overdose of the antacid? Refer to the hydrochloric acid concentration in the stomach in your answer.
- A certain antacid tablet contains [latex]\scriptsize \displaystyle 22.0\text{ g}[/latex] of baking soda ([latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex]). It is used to neutralise the excess hydrochloric acid in the stomach. The balanced equation for the reaction is:
[latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{{\text{3}\left( \text{s} \right)}}}\text{+HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\to \text{NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
The hydrochloric acid in the stomach has a concentration of [latex]\scriptsize \displaystyle 1.0\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex].
Calculate the volume of the hydrochloric acid that can be neutralised by the antacid tablet. - A learner finds some sulfuric acid solution in a bottle labelled ‘dilute sulfuric acid’. He wants to determine the concentration of the sulfuric acid solution. To do this, he decides to titrate the sulfuric acid against a standard potassium hydroxide ([latex]\scriptsize \displaystyle \text{KOH}[/latex]) solution.
- What is a standard solution?
- Calculate the mass of [latex]\scriptsize \displaystyle \text{KOH}[/latex] which he must use to make [latex]\scriptsize \displaystyle 300\text{ c}{{\text{m}}^{3}}[/latex] of a [latex]\scriptsize \displaystyle 0.2\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}\text{ KOH}[/latex] solution.
- Write a balanced chemical equation for the reaction between [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] and [latex]\scriptsize \displaystyle \text{KOH}[/latex].
- During the titration the learner finds that [latex]\scriptsize \displaystyle 15\text{ c}{{\text{m}}^{\text{3}}}[/latex] of the solution [latex]\scriptsize \displaystyle \text{KOH}[/latex] neutralises [latex]\scriptsize \displaystyle 20\text{ c}{{\text{m}}^{\text{3}}}[/latex] of the [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] solution. Calculate the concentration of the [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] solution.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
- Concentrated. There are many more moles of the base than the solvent.
- Dilute. There are many more moles of the solvent than the acid.
- .
- You have the volume (V) and the mass (m). You need the number of moles (n) and the molar mass (M).
[latex]\scriptsize \displaystyle \begin{align*} \displaystyle {M}_{{\text{(}{{\text{Na}}}\text{H}{{\text{CO}}_{\text{3}}}\text{)}}}&=23+1.01+12+\left( {3\text{ x }16} \right)=84.01\text{ g}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\ {n}_{{\text{(}{{\text{Na}}}\text{H}{{\text{CO}}_{\text{3}}}\text{)}}}&=\displaystyle \frac{m}{M}=\displaystyle \frac{{27}}{{84.01}}\text{= }0.32\text{ mol}\\ V&=22,6\text{ c}{{\text{m}}^{\text{3}}}\times \displaystyle \frac{{0.001\text{ }}}{1}=0.0226\text{ d}{{\text{m}}^{\text{3}}}\\ {c}_{{\text{(}{{\text{Na}}}\text{H}{{\text{CO}}_{\text{3}}}\text{)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.32}}{{0.0226}}\text{= }14.16\text{ mol}\text{.d}{{\text{m}}^{\text{-}}}^{\text{3}} \\ \end{align*}[/latex] - You have the volume (V) and number of moles (n). You can calculate the concentration.
[latex]\scriptsize \displaystyle {{c}_{{\left( {{{H}_{3}}P{{O}_{4}}} \right)}}}=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.893}}{{4.79}}\text{ }=0.186\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
- You have the volume (V) and the mass (m). You need the number of moles (n) and the molar mass (M).
Exercise 1.2
- Acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]) + metal ([latex]\scriptsize \displaystyle \text{Ca}[/latex]) → salt + hydrogen
Anion (from acid) is [latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{\text{-}}}[/latex], cation (from metal) is[latex]\scriptsize \displaystyle \text{C}{{\text{a}}^{{\text{2+}}}}[/latex]. Therefore salt is[latex]\scriptsize \displaystyle \text{CaC}{{\text{l}}_{\text{2}}}[/latex].
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ C}{{\text{a}}_{{\left( \text{s} \right)}}}\to \text{CaC}{{\text{l}}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+ }{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
To balance this equation there must be two [latex]\scriptsize \displaystyle \text{HCl}[/latex] molecules.
[latex]\scriptsize \displaystyle \text{2HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ C}{{\text{a}}_{{\left( \text{s} \right)}}}\to \text{CaC}{{\text{l}}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+ }{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}[/latex] - acid ([latex]\scriptsize \displaystyle \text{HCl}[/latex]) + metal hydroxide ([latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{\text{2}}}[/latex]) → salt + water
Anion (from acid) is [latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{\text{-}}}[/latex], cation (from metal) is [latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex]. Therefore salt is[latex]\scriptsize \displaystyle \text{MgC}{{\text{l}}_{\text{2}}}[/latex].
[latex]\scriptsize \displaystyle \text{HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+Mg}{{\left( {\text{OH}} \right)}_{{\text{2}\left( \text{s} \right)}}}\to \text{MgC}{{\text{l}}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
To balance this equation there must be two [latex]\scriptsize \displaystyle \text{HCl}[/latex] molecules and two [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{O}[/latex] molecules.
[latex]\scriptsize \displaystyle \text{2HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+Mg}{{\left( {\text{OH}} \right)}_{{\text{2}\left( \text{s} \right)}}}\to \text{MgC}{{\text{l}}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+ 2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex] - acid ([latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex]) + metal oxide ([latex]\scriptsize \displaystyle \text{MgO}[/latex]) → salt + water
Anion (from acid) is [latex]\scriptsize \displaystyle \text{S}{{\text{O}}_{\text{2}}}^{{\text{4-}}}[/latex], cation (from metal) is [latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex].
Therefore salt is [latex]\scriptsize \displaystyle \text{MgS}{{\text{O}}_{\text{4}}}[/latex].
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+Mg}{{\text{O}}_{{\left( \text{s} \right)}}}\to \text{MgS}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+ }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex]
This equation is balanced.
Exercise 1.3
- We need the mass of oxalic acid. However, we don’t know the number of moles yet.
[latex]\scriptsize \begin{align*} \displaystyle V&=500\text{ c}{{\text{m}}^{\text{3}}}\times \displaystyle \frac{{0.001}}{1}=0.5\text{ d}{{\text{m}}^{\text{3}}}\\ n&=c\text{x}V\\ n&=0.2\text{ x }0.5=0.1\text{ mol}\\ {M}_{{\text{(}{{\text{H}}_{\text{2}}}\text{C}_{2}{{\text{O}}_{\text{4}}}\text{)}}}&=\left( {2\text{x}1.01+2\text{x}12,0+4\text{x}16.0} \right)=90.02\text{ g}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\ m&=nM\\ m&=0.1\text{ x }90.02=9.00\text{ g} \end{align*}[/latex] - The balanced equations is:
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}{{\text{C}}_{\text{2}}}{{\text{O}}_{\text{4}}}\text{ + 2NaOH}\to \text{N}{{\text{a}}_{\text{2}}}{{\text{C}}_{\text{2}}}{{\text{O}}_{\text{4}}}\text{ + 2}{{\text{H}}_{\text{2}}}\text{O}[/latex]
The number of moles of oxalic acid used is the number of moles in [latex]\scriptsize \displaystyle 40\text{ c}{{\text{m}}^{\text{3}}}[/latex] of the standard solution:
[latex]\scriptsize \displaystyle \begin{align*} V&=40\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}=0.04\text{ d}{{\text{m}}^{\text{3}}}\\ n&=\text{cx}V=0.2\text{ x }0.04=0.008\text{ mol} \end{align*}[/latex]
The molar ratio of oxalic acid to sodium hydroxide is [latex]\scriptsize \displaystyle 1:2[/latex]. For everyone mole of oxalic acid there are two moles of sodium hydroxide.
[latex]\scriptsize \displaystyle \begin{align*} {{n}_{{\left( {\text{NaOH}} \right)}}}&=2\times 0,008=0.016\text{ mol}\\ {{V}_{{\left( {\text{NaOH}} \right)}}}&=35\text{ c}{{\text{m}}^{\text{3}}}\times \displaystyle \frac{{0,001\text{ }}}{1}=0.035\text{ d}{{\text{m}}^{\text{3}}}\\ {{c}_{{\left( {\text{NaOH}} \right)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.016}}{{0.035}}=0.46\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex]
Unit 1: Assessment
- .
- You have the volume (V) and the mass (m). You need the number of moles (n) and the molar mass (M).
[latex]\scriptsize \displaystyle \begin{align*} {{M}_{{\left( {\text{HCl}} \right)}}}&=1.01+35.45=36.46\text{ g}\text{.mo}{{\text{l}}^{{-1}}}\\ {{m}_{{\left( {\text{HCl}} \right)}}}&=32.8\text{ mg }\times \displaystyle \frac{{0.001}}{1}\text{ }=0.0328\text{ g}\\ {{n}_{{\left( {\text{HCl}} \right)}}}&=\displaystyle \frac{m}{M}=\displaystyle \frac{{0.0328}}{{36.46}}\text{= }9.0\times {{{10}}^{{-4}}}\text{ mol}\\ V&=12,76\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}\text{= }0.01276\text{ d}{{\text{m}}^{3}}\\ {{c}_{{\left( {\text{HCl}} \right)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{9.0\times {{{10}}^{{-4}}}}}{{0.01276\text{ }}}=\text{ }0.07\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex] - You have the volume (V) and original concentration of the ammonia solution, you need the number of moles (n) in that original solution.
[latex]\scriptsize \displaystyle c=\displaystyle \frac{n}{V}[/latex]. Therefore [latex]\scriptsize \displaystyle n=c\text{ x }V[/latex]
[latex]\scriptsize \displaystyle {{n}_{{\left( {\text{original solution of N}{{\text{H}}_{\text{3}}}} \right)\text{ }}}}\text{= 6}\text{.54 x 1,12 = 7}\text{.32 mol}[/latex]
The final volume used to calculate the concentration must be the volume of the water plus the volume of ammonia added.
[latex]\scriptsize \displaystyle \begin{align*} {{V}_{{\left( {\text{total}} \right)}}}&=0.50+1.12=1.62\text{ d}{{\text{m}}^{3}}\\ {{c}_{{\left( {\text{final solution of NH}_{3}} \right)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{7.32}}{{1.62}}=4.52\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex]
- You have the volume (V) and the mass (m). You need the number of moles (n) and the molar mass (M).
- .
- metal carbonate + acid → salt + carbon dioxide + water
The cation will be from the metal ([latex]\scriptsize \displaystyle \text{N}{{\text{a}}^{+}}[/latex]), the anion will be from the acid ([latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{\text{-}}}[/latex]). Therefore the salt will be NaCl.
[latex]\scriptsize \displaystyle \text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{{\text{3}\left( {\text{aq}} \right)}}}\text{+2HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\to \text{2NaC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\text{+ C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\text{+ }{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( l \right)}}}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*} n&=\text{ c}\times V\\ {V}_{{\text{(}{{\text{Na}_{2}}}{{\text{CO}}_{\text{3}}}\text{)}}}&=25.0\text{ c}{{\text{m}}^{3}}\times \displaystyle \frac{{0.001}}{1}=0.0250\text{ d}{{\text{m}}^{\text{3}}}\\ {n}_{{\text{(}{{\text{Na}_{2}}}{{\text{CO}}_{\text{3}}}\text{)}}}&=c\text{ x }V=0.1\text{x }0.0250=0.0025\text{ mol} \end{align*}[/latex]
From the balanced equation for every [latex]\scriptsize \displaystyle 1[/latex] mol of [latex]\scriptsize \displaystyle \text{N}{{\text{a}}_{\text{2}}}\text{C}{{\text{O}}_{\text{3}}}[/latex] there are [latex]\scriptsize \displaystyle 2[/latex] mol [latex]\scriptsize \displaystyle \text{HCl}[/latex].
[latex]\scriptsize \displaystyle \begin{align*} {{n}_{{\left( {\text{HCl}} \right)}}}&=2\text{ x }0.0025=0.005\text{ mol}\\ {{V}_{{\left( {\text{HCl}} \right)}}}&=35.0\text{ d}{{\text{m}}^{\text{3}}}\times \displaystyle \frac{{0.001}}{1}=0.0350\text{ d}{{\text{m}}^{\text{3}}}\\ {{c}_{{\left( {\text{HCl}} \right)}}}&=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.005}}{{0.0350}}\text{ = }0.143\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}} \end{align*}[/latex]
- metal carbonate + acid → salt + carbon dioxide + water
- .
- base + acid → salt + water
The cation (from the base) is [latex]\scriptsize \displaystyle \text{M}{{\text{g}}^{{\text{2+}}}}[/latex]. The anion (from the acid) is [latex]\scriptsize \displaystyle \text{C}{{\text{l}}^{-}}[/latex].
Therefore the salt is [latex]\scriptsize \displaystyle \text{MgC}{{\text{l}}_{\text{2}}}[/latex]
[latex]\scriptsize \displaystyle \text{Mg}{{\left( {\text{OH}} \right)}_{{\text{2}\left( \text{s} \right)}}}\text{+2HC}{{\text{l}}_{{\left( {\text{aq}} \right)}}}\to \text{MgC}{{\text{l}}_{{\text{2}\left( {\text{aq}} \right)}}}\text{+2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex] - Adults have a bigger mass and generally produce more acid than children. Adults will therefore need more antacid to neutralise the excess acid. If children were to take the same dosage as adults, they would have excess base in their stomach.
- A low acid concentration (pH too high) in the stomach may slow down food digestion or may cause further stomach upset.
- base + acid → salt + water
- .
[latex]\scriptsize \displaystyle \begin{align*} {M}_{{\text{(}{{\text{Na}}}\text{HC}{{\text{O}}_{\text{3}}}\text{)}}}&=23\text{.0 + 1}\text{.01 + 12}\text{.0 + }\left( {\text{3 x 16}\text{.0}} \right)\text{ = 84}\text{.01 g}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\ {n}_{{\text{(}{{\text{Na}}}\text{HC}{{\text{O}}_{\text{3}}}\text{)}}}&=\displaystyle \frac{m}{M}\\ n&=\displaystyle \frac{{\text{22}\text{.0}}}{{\text{84}\text{.01}}}\text{= 0}\text{.26 mol} \end{align*}[/latex]
From the balanced equation we see that the molar ratio of [latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{{\text{3 }}}}\text{to HCl is 1:1}[/latex].
Therefore:
[latex]\scriptsize \displaystyle \begin{align*} {{n}_{{\left( {\text{HCl}} \right)}}}&={n}_{{\text{(}{{\text{Na}}}\text{HC}{{\text{O}}_{\text{3}}}\text{)}}}=0\text{.26 mol}\\ c&=\displaystyle \frac{n}{V}\text{ therefore }V=\displaystyle \frac{n}{c}\\ {{V}_{{\left( {\text{HCl}} \right)}}}&=\displaystyle \frac{{\text{0}\text{.26}}}{{\text{1}\text{.0 }}}\text{ = 0}\text{.26 d}{{\text{m}}^{\text{3}}} \end{align*}[/latex] - .
- A standard solution is a solution that contains a precisely known concentration of a substance. This substance can then be used in titrations.
- .
[latex]\scriptsize \displaystyle \begin{align*} {{V}_{{\left( {\text{KOH}} \right)}}}&=300\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}\text{ = }0,3\text{ d}{{\text{m}}^{\text{3}}}\\ n&=c\text{ x }V\\ {{n}_{{\left( {\text{KOH}} \right)}}}&=0.2\text{ x }0.3=0.06\text{ mol}\\ {{M}_{{\left( {\text{KOH}} \right)}}}&=\left( {39.1\text{ }+\text{ }16.0\text{ }+\text{ }1.01} \right)=56.11\text{ g}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\ m&=n\text{x}M\\ {{m}_{{\left( {\text{KOH}} \right)}}}&=0.06\text{ x }56.11\text{ }=3.37\text{ g} \end{align*}[/latex] - Sulfuric acid is a strong acid and potassium hydroxide is a strong base, therefore the equation is:
[latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+2KO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to {{\text{K}}_{\text{2}}}\text{S}{{\text{O}}_{{\text{4}\left( {\text{aq}} \right)}}}\text{+2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}[/latex] - .
[latex]\scriptsize \displaystyle {{V}_{{\left( {\text{KOH}} \right)}}}=15\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0,001}}{1}=0.015\text{ d}{{\text{m}}^{\text{3}}}[/latex]
The number of moles of [latex]\scriptsize \displaystyle \text{KOH}[/latex] used to neutralise the [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}[/latex] is:
[latex]\scriptsize \displaystyle {{n}_{{\left( {\text{KOH}} \right)}}}\text{= c x V = 0}\text{.2 x 0}\text{.015 = 0}\text{.003 mol}[/latex]
From the balanced equation we see that the mole ratio of [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}\text{ to KOH is 1:2}[/latex]. There is one mole of sulfuric acid for every two moles of potassium hydroxide.
.
[latex]\scriptsize \displaystyle \begin{align*} {n}_{{\text{(}{{\text{H}_{2}}}{{\text{SO}}_{\text{4}}}\text{)}}}&=\displaystyle \frac{{0.003}}{2}=0.0015\text{ mol}\\ {V}_{{\text{(}{{\text{H}_{2}}}{{\text{SO}}_{\text{4}}}\text{)}}}&=20\text{ c}{{\text{m}}^{\text{3}}}\text{ }\times \displaystyle \frac{{0.001}}{1}0.020\text{ d}{{\text{m}}^{\text{3}}} \end{align*}[/latex]
Therefore, the concentration of the sulfuric acid is:
[latex]\scriptsize \displaystyle {{c}_{{\left( {{{\text{H}}_{\text{2}}}\text{S}{{\text{O}}_{\text{4}}}} \right)}}}=\displaystyle \frac{n}{V}=\displaystyle \frac{{0.0015\text{ }}}{{0.020}}=0,075\text{ mol}\text{.d}{{\text{m}}^{{\text{-3}}}}[/latex]
Media Attributions
- Fig 1 © Siyavula is licensed under a CC BY-NC (Attribution NonCommercial) license
- Fig 2 © DHET is licensed under a CC BY (Attribution) license
- Fig 3 © DHET is licensed under a CC BY (Attribution) license
- Fig 4 © libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 5 © Stephen Lower is licensed under a CC BY (Attribution) license
- Fig 6 © Siyavula is licensed under a CC BY-NC (Attribution NonCommercial) license
- Fig 7 © libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 8 © libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
describes a substance that can act as an acid in one reaction, or a base in another reaction
describes a substance that can donate a proton in one reaction or accept a proton in another reaction
: a solution where there is a high ratio of dissolved substance (e.g. acid or base) to solvent
a solution where there is a low ratio of dissolved substance to solvent
a solution where the exact concentration of solute in a solvent is known
a neutral ionic compound composed of cations and anions
when a stoichiometrically equivalent number of moles of both reactants has been added to the reaction vessel
a reaction that involves an acid and a base reacting to form a salt
a measure of the acidity or alkalinity of a solution
the method used to determine the concentration of a known substance using another, standard solution
